一文带你彻底拿下a，b两点间等效电阻

对于涉及电路的专业课的同学们，关于求解两点间等效电阻是一个重点知识！接下来博主带你一文彻底拿下等效电阻问题！

前言

等效电阻的应用使得我们在进行电路简化计算中起到非常重要的作用，比如我们进行戴维南等效求等效电阻时，或者在三要素法中求解 τ =RC 时用到。

接下来博主带你拿下等效电阻问题！只要按着步骤走，一切问题都没有！

🐔等效电阻计算步骤

情况一： a，b两点间有直接相连的电阻

• 先找到直接相连的电阻
• 然后基于这个直接相连的电阻，找到两个端点互相相连的电阻进行并联
• 将各支路中首尾相连的电阻进行串联
• 简化成功

情况二： a，b两点间没有直接相连的电阻

• 从a，b端口开始标注每一个节点（给每个节点起名字，相同的节点起一样的名字）
• 将两个端口相对应的电阻进行并联
• 将相互串联的两个电阻进行合并
• 简化成功

这种方法也可以求解第一种情况，这种方法属于万金油！

🐬实例讲解

🐸TEST 1

求取下图a，b间等效电阻

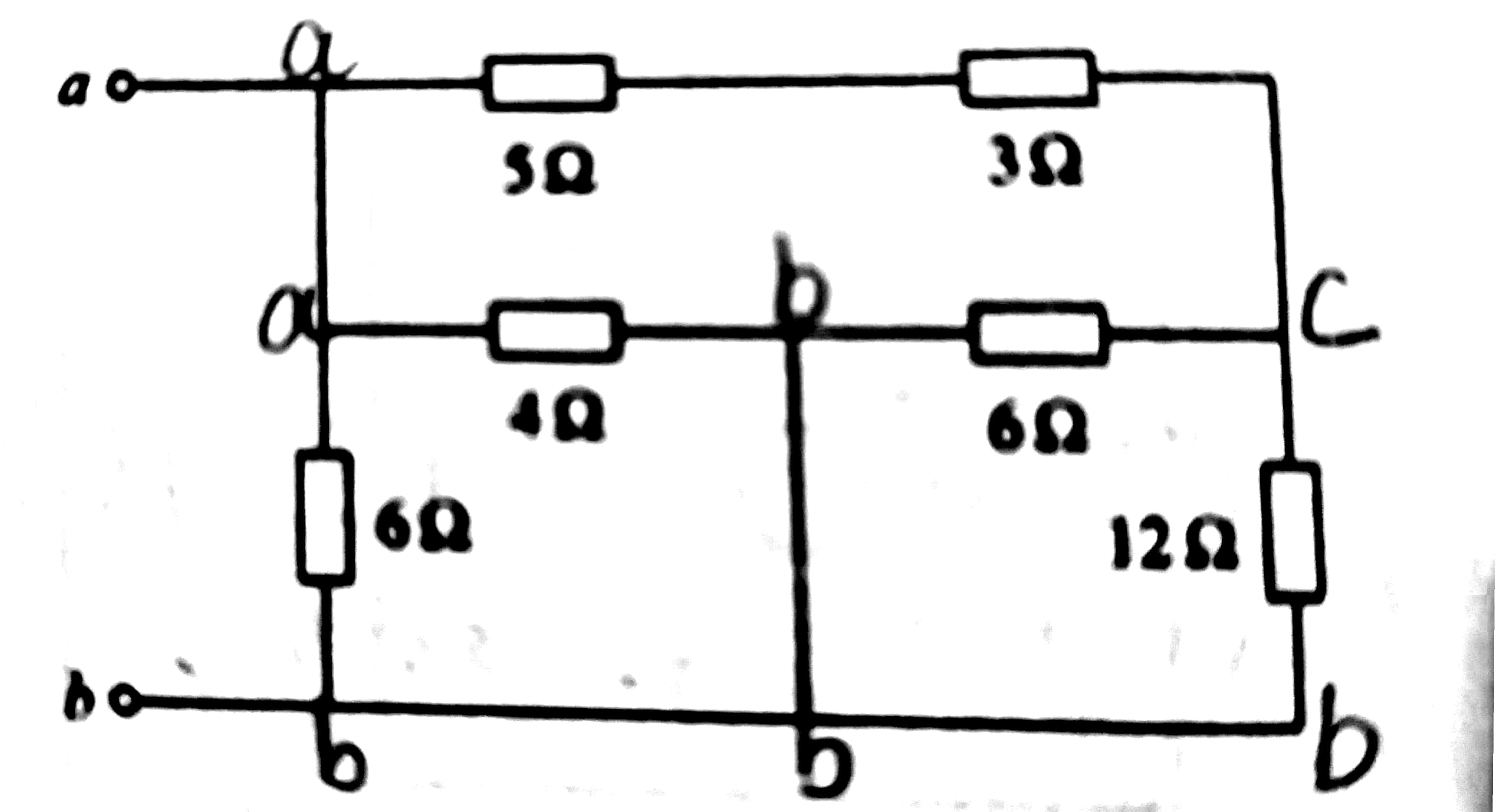
分析：
此题目可以用第一种方法求解，也可以用第二种。
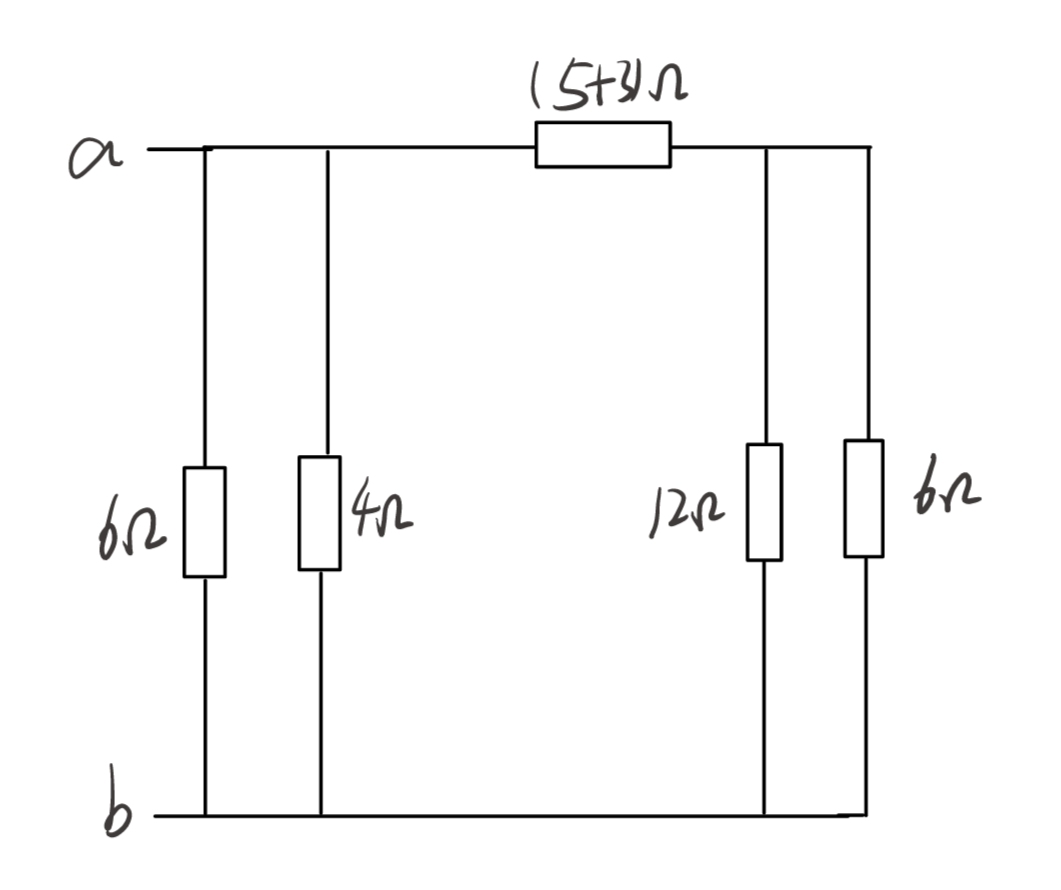
第一种方法 ： 我们看到a，b间有直接相连的电阻1，那么以1为基准，我们看到4和5是串联，所以两者相加为8Ω，我们看到3和6两个端点对应连接为并联，结果为2Ω，而且1和2也是并联关系为12/5，然后我们发现化简后就是8Ω串联上2Ω然后并联12/5Ω，最后Rab=2Ω。

第二种方法： 我们将各个节点进行标号，如上述图像所示，我们可以很轻松的看出来串并联，（1，2）和（3，6）并联，（4，5）串联，然后（4，5）整体与（3，6）串联，然后与（1，2）并联。

另法： 我们可以发现有两对节点是重合的，左上方的两个a和中间的两个b，这两对点是可以捏成一个点的。
我们可以将b，b线切开，分成两个线分别连接至b节点。

🐸TEST 2

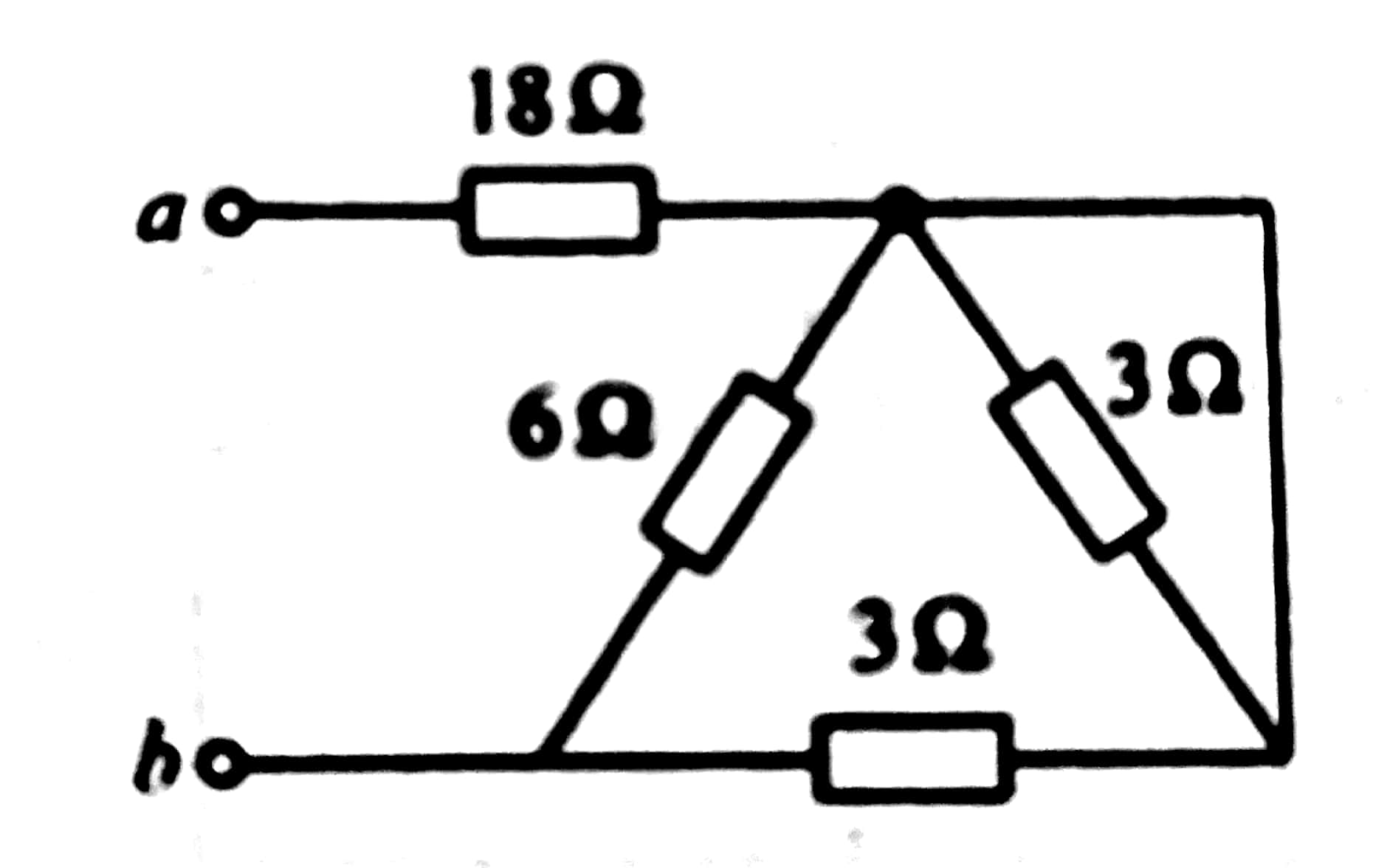
解题思路： a，b之间没有直接相连的电阻，那么通过观察，我们可以看到电阻4的两端连接的节点相同即为被短接，电阻2和3的两端互相连接，所以2和3并联，最后a，b间电阻就是18Ω+6//3=20Ω

🦁总结

电阻等效的求法很多，大差不差就是找到并联部分，找到串联部分，其实电阻之间相连的是导线，导线可以移动，只要不破坏端点位置，我们可以任意移动，所以只要在我们移动后发现两个电阻为并联关系，我们可以直接进行并联等效。