扩散模型（二）——DDPM详解

最新推荐文章于 2025-09-13 11:37:19 发布

原创最新推荐文章于 2025-09-13 11:37:19 发布 · 2.2k 阅读

64 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #机器人 #具身智能

具身智能算法基础专栏收录该内容

17 篇文章

订阅专栏

上一篇笔记先综述了一下扩散模型，这一篇详细分析一下扩散模型的训练和采样算法，以及其中的数学推理

目前我们常说的“扩散模型”，基本都是从 Ho 等人在 2020 年提出的 DDPM（Denoising Diffusion Probabilistic Model）这个方法开始流行起来的。虽然名字叫“扩散模型”，但DDPM 实际上和传统的物理扩散模型有很大区别，两者只是名字和表面形式有点像，实质上是完全不同的两套体系

传统的扩散模型（比如基于“朗之万方程”、能量函数和得分匹配的方法）是一套基于物理过程、统计物理和概率理论的生成模型体系，这类方法依赖于具体的能量函数推导和 Langevin 动力学。而 DDPM 其实并不直接用这些传统概念。与其说它是“扩散模型”，不如说是一种“渐变模型”或“逐步添加噪声再逆过程还原”的模型。换句话说，DDPM 只是借用了扩散的“逐步变化”过程，但在实现机制和理论基础上和早期的扩散模型几乎没关系。

早在 2015 年，ICML 上的一篇论文《Deep Unsupervised Learning using Nonequilibrium Thermodynamics》中已经提出了类似的数学框架。但直到 Ho 等人在 2020 年把这种方法应用到高分辨率图像生成，并调试出效果，才真正引发了后续大规模研究的热潮

核心参考：Denoising Diffusion Probabilistic Models

1 基本概念

2 前向加噪过程 Forward diffusion process

2.1 重参数化技巧

2.2 高斯分布合并规则

2.3 与随机梯度 Langevin 动力学的联系

3 反向去噪过程 Reverse diffusion process

3.7 VLB 逐项拆解为可计算的KL和熵项

3.8 训练损失的参数化

3.9 简化（Simplification）

3.10 训练与采样算法流程伪代码

4 参考资料

1 基本概念

简而言之，DDPM就是让图片一步步变成噪声，然后教AI如何把噪声一步步还原成高清图片

更具体一点，有一张好照片：

正向过程：每次往里加点噪声（就是一点点“雪花”），加很多次，最后变成完全的雪花噪声图
逆向过程：现在AI要学会拿一张雪花噪声图，能不能一步步把噪声去掉，最终还原成原来的好照片
训练过程：不是让AI直接猜原图，而是教它“每次要去掉什么样的噪声”。这就像教AI修图，每一步修正哪里，修多少

DDPM这篇论文把“图像变噪声-再还原”的过程玩明白了，找到一种更好教AI画画的新方式，不仅生成图片更好，而且背后的数学和理论也更严密

接下来开始理论部分：

首先从架构上来说，DDPM 模型主要包括两个阶段：

前向加噪过程 Forward diffusion process：将原始数据 $\mathbf{x}_0$ 作为起始点，每一步为其添加足够小的高斯噪声，经过足够多的步骤 T，使得 $\mathbf{x}_0$ 最终符合标准高斯分布
反向去噪过程 Reverse diffusion process：试图从噪声数据中恢复出有用的数据。因为前向过程是可行的，所以理论上反向去噪过程也是可行的，这两个过程互为逆操作

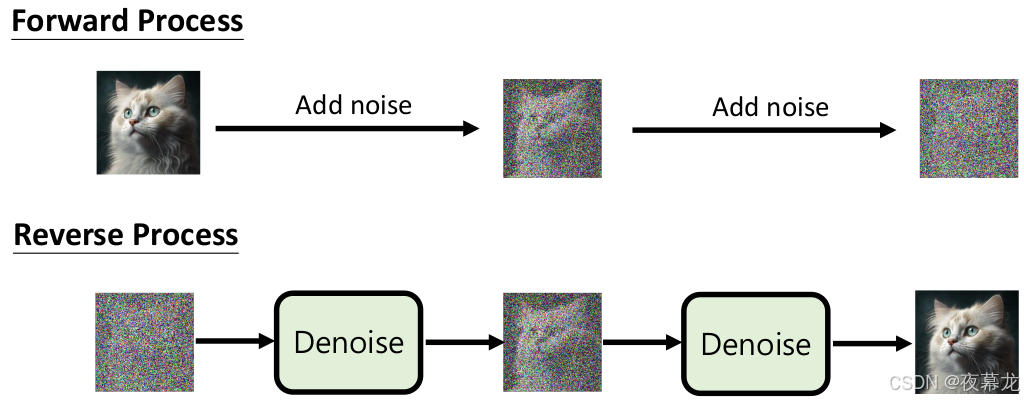
图 1. Overview of DDPM

2 前向加噪过程 Forward diffusion process

在扩散模型中，前向扩散（Forward Diffusion）指的是从原始数据 $x_0$ （服从分布 $q(x_0)$ ）出发，逐步向样本中注入小量高斯噪声，从而在 T 个离散步骤内生成一系列噪声化样本 $\{x_1, x_2, \dots, x_T\}$ 。注入噪声的幅度由一个方差调度（Variance Schedule） $\{\beta_t\}_{t=1}^T$ 控制，其近似后验分布（前向过程/扩散过程）被固定为一个马尔可夫链，具体可写为：

$\quad q(x_t \mid x_{t-1}) \;=\; \mathcal{N}\!\bigl(x_t;\, \sqrt{1-\beta_t}\,x_{t-1},\, \beta_t \mathbf{I}\bigr)$

$q(x_{1:T} \mid x_0) \;=\; \prod_{t=1}^{T} q(x_t \mid x_{t-1})$

其中 $\beta _t$ 是一个较小的超参数，通常会随着 t 增大而增大。经过多次噪声累加后，当 $T \to \infty$ 时， $x _ T$ 将接近各向同性高斯分布

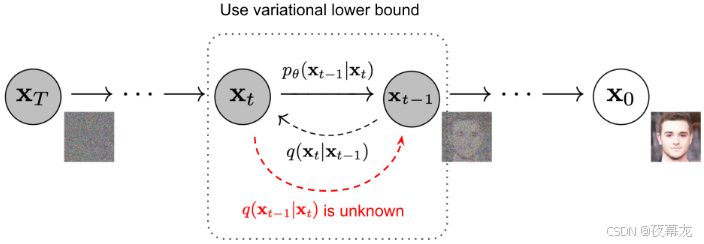
图 2. 通过逐步添加（去除）噪声生成样本的前向（反向）扩散过程的马尔可夫链

2.1 重参数化技巧

前向扩散具有一个颇为实用的性质：我们可以直接使用重参数化技巧（Reparameterization Trick）在任意时间步 t 对 $x_{t}$ 进行闭式采样，无需逐步采样所有中间状态。令 $\alpha_t = 1 - \beta_t$ 并定义 $\bar{\alpha}_t = \prod_{i=1}^{t}\alpha_i$ ，则有：

$\mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1}$

继续递归展开得：

$\mathbf{x}_t = \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}}\,\bar{\boldsymbol{\epsilon}}_{t-2} \quad \text{}\;\boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$

一直展开下去，直至初始状态：

$\mathbf{x}_t = \cdots = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\,\boldsymbol{\epsilon}$

因此条件概率分布可以写成：

$q(\mathbf{x}_t \mid \mathbf{x}_0) = \mathcal{N}\bigl(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t}\,\mathbf{x}_0,\,(1 - \bar{\alpha}_t)\mathbf{I}\bigr)$

2.2 高斯分布合并规则

此处应注意，当合并两个不同方差的高斯分布 $\mathcal{N}(\mathbf{0},\sigma_1^2\mathbf{I})$ 与 $\mathcal{N}(\mathbf{0},\sigma_2^2\mathbf{I})$ ，新分布为：

$\mathcal{N}\Bigl(\mathbf{0},\,(\sigma_1^2 + \sigma_2^2)\mathbf{I}\Bigr)$

在上述推导中，合并后的标准差是：

$\sqrt{(1 - \alpha_t) + \alpha_t (1 - \alpha_{t-1})} = \sqrt{1 - \alpha_t \alpha_{t-1}}$

通常，当样本噪声较大时，可以采用更大的更新步长，因此设定 $\beta_1 < \beta_2 < \cdots < \beta_T$ ，也就对应着：

$\bar{\alpha}_1 > \bar{\alpha}_2 > \cdots > \bar{\alpha}_T$

2.3 与随机梯度 Langevin 动力学的联系

Langevin 动力学是源自物理学的概念，最初用于分子系统的统计建模。当与随机梯度下降（SGD）相结合时，随机梯度 Langevin 动力学（Stochastic Gradient Langevin Dynamics，简称SGLD，Welling & Teh 2011）可以通过以下的马尔可夫链更新规则，仅用梯度信息 $\nabla_{\mathbf{x}}\log p(\mathbf{x})$ 来采样目标分布 $p(\mathbf{x})$ ：

$\mathbf{x}_t = \mathbf{x}_{t-1} + \frac{\delta}{2} \nabla_{\mathbf{x}} \log p(\mathbf{x}_{t-1}) + \sqrt{\delta}\,\boldsymbol{\epsilon}_t, \quad \text{}\;\boldsymbol{\epsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$

其中 δ 是步长。当满足 $T \to \infty$ ， $\epsilon \to 0$ 时， $\mathbf{x}_T$ 将精确地收敛于概率密度 $p(\mathbf{x})$

相较于标准随机梯度下降（SGD），随机梯度 Langevin 动力学通过在参数更新中加入高斯噪声，避免了陷入局部极小值的问题

3 反向去噪过程 Reverse diffusion process

如果能够逆转上述前向过程，并从 $q_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 进行采样，就可以从高斯噪声输入 $x_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 重现真实样本 $x_{0}$ 。此处应注意，当 $\beta_t$ 足够小时， $q(\mathbf{x}_{t-1}|\mathbf{x}_t)$ 也服从高斯分布

但是，我们无法估计 $p_\theta(x_{t-1} \mid x_t)$ ，因为它需要使用整个数据集。我们的目标是学习一个模型，去近似这些条件概率，从而可以基于噪声来生成新样本

图 3. An example of training a diffusion model for modeling a 2D swiss roll data

前向轨迹定义如下，当以 $x_0$ 为条件时，反向条件概率是可解的：

$q(x_{t-1} | x_t, x_0) = \mathcal{N}(x_{t-1};\, \tilde{\mu}(x_t, x_0),\, \tilde{\beta}_t I)$

也就是说，已知最终的数据样本 $x_0$ 时，逆向一步的采样（扩散过程的反推）是一个高斯分布，其均值和方差是有明确解析解的

使用贝叶斯法则（Bayes’ rule），得到一步逆向的条件概率：

$q(x_{t-1}|x_t, x_0) = \frac{q(x_t|x_{t-1}, x_0)\, q(x_{t-1}|x_0)}{q(x_t|x_0)}$

推导过程：

3.1 联合分布的拆分和指数化

所有项都是高斯分布，利用高斯分布的形式拆开，最终可以写成：

$\propto \exp\left( -\frac{1}{2} \left( \frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}} x_0)^2}{1 - \bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_t} x_0)^2}{1 - \bar{\alpha}_t} \right) \right )$

3.2 展开合并同类项

对平方项展开并整理，得：

$= \exp\left( -\frac{1}{2} \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right) x_{t-1}^2 - \left( \frac{2\sqrt{\alpha_t}}{\beta_t} x_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} x_0 \right) x_{t-1} + C(x_t, x_0) \right)$

其中 $C(x_t, x_0)$ 是和 $x_{t-1}$ 无关的常数项，通常省略不写

3.3 配方还原高斯

将上述二次型重新写成标准高斯分布的形式，从而得到它的均值和方差：

（1）方差参数

$\begin{aligned} \tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}) = \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \end{aligned}$

这个量实际是反向采样的高斯分布的方差

$\beta_t$ 是正向扩散中的噪声系数
$\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$ 是从 0 到 t 的累计残留信号比例

（2）均值参数

$\begin{aligned} \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\ &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned}$

这个表达式说明了，逆过程每一步采样的均值是当前 noisy 状态和原始数据 $x_0$ 的线性组合，权重与噪声 schedule 有关

3.4 结合 x₀ 的表示进一步推导

由于在训练过程中，通常没有 $x_0$ 的真实值，只能用模型预测，或用当前 noisy 样本和噪声的表达式表示，根据 nice property 可以表示：

$x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} (x_t - \sqrt{1 - \bar{\alpha}_t} \, \epsilon_t)$

将这个公式带入前面的 $\tilde{\mu}$ 中，得到最终在网络训练时用到的表达式：

$\begin{aligned} \tilde{\boldsymbol{\mu}}_t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\ &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \end{aligned}$

每一步的逆扩散都是“给定当前 noisy 样本 $x_t$ ，结合噪声预测/残差，往回还原一点点”，一步步把噪声变成数据

由于整个推导过程可微，且采样均值方差有解析表达，训练和采样都很高效

如图 2 所示，这种 setup 与 VAE 很相似，因此可以采用变分下界（Variational Lower Bound, VLB）来优化对数似然

3.5 变分下界与负对数似然

（1）负对数似然的变分下界推导

我们希望优化 $-\log p_\theta(\mathbf{x}_0)$ ，但由于 $p_\theta(\mathbf{x}_0)$ 难以直接计算，所以利用变分推断，用一个辅助分布 $q(\mathbf{x}_{1:T}|\mathbf{x}_0)$ 对联合分布进行近似，从而推导下界，详细推导：

$\begin{aligned} - \log p_\theta(\mathbf{x}_0) &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) & \small{\text{; KL is non-negative}}\\ &= - \log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\ &= - \log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\ &= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ \text{Let }L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \end{aligned}$

a. KL 散度 $D_\text{KL}$ 总是非负，所以这提供了下界

b. KL 散度本质上是 q下 log(q/p) 的期望，这里 p 分母多一个 $p_\theta(\mathbf{x}_0)$ 是因为联合概率分布的边缘化

c. 到第三步的继续化简得到两个部分，其中 $\log p_\theta(\mathbf{x}_0)$ 可以单独拿出来

d. 合并前后两项，负对数似然被下界 $L_\text{VLB}$ 所近似

e. $L_\text{VLB}$ 就是我们最后优化的目标，它是对真实数据的负对数似然的下界

3.6 Jensen 不等式的等价推导

同样可以用Jensen不等式（即凸函数的期望不小于期望的函数值）推导得到一样的结果，假设我们想要最小化交叉熵作为学习目标重新推导：

$\begin{aligned} L_\text{CE} &= - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \mathbb{E}_{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big) \\ &\leq - \mathbb{E}_{q(\mathbf{x}_{0:T})} \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \\ &= \mathbb{E}_{q(\mathbf{x}_{0:T})}\Big[\log \frac{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{0:T})} \Big] = L_\text{VLB} \end{aligned}$

a. 交叉熵就是负对数似然

b. $\mathbf{x}_0$ 的概率需要对所有潜变量边缘化，难以直接计算

c. 引入辅助分布 q，构造重要性采样公式

d. Jensen不等式，将 log 移到积分外部，得到下界

e. 得到的下界和前面的VLB一致，表明两种推导方式是等价的

3.7 VLB 逐项拆解为可计算的KL和熵项

为了让上面的每一项都能被具体计算，将 VLB 进一步拆解为每一步KL散度和熵项的和

为了使方程中的每一项都可解析计算，目标函数 VLB 可以进一步改写为多个 KL 散度和熵项的组合（具体步骤详见 Sohl-Dickstein 等人2015年论文附录 B）：

$\begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\ &= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \end{aligned}$

a. 联合概率分布都可以写成条件概率的连乘

b. 拆分成最后一项的负对数概率和每一步的条件概率比值

c. 第一步和最后一步单独提取，方便后续和训练目标对应。

让我们分别标注变分下界损失中的每个组成部分，按KL散度分组最后整理得到：

$\begin{aligned} L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\ \text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\ L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\ L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \end{aligned}$

变分下界中的每一项 KL 散度（除了 $L_0$ ）都在比较两个高斯分布，因此可以解析计算。而 $L_T$ 是常数项且在训练时可以忽略，因为 q 没有可学习参数且 $\mathbf{x}_T$ 是高斯噪声。Ho等人（2020）使用一个从 $\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1))$ 派生的离散解码器来单独建模 $L_0$

每一步的损失都具有明确的概率论意义，可以通过采样和预测得到

上述推导展示了如何将 DDPM 的训练目标转化为每一步的KL损失和重建损失的和

每个 KL 项本质上衡量了“正向扩散”和“反向去噪”在每个时间步的分布差异

训练过程中，实际采样和预测只需优化这些明确的概率分布距离，因此易于实现和收敛

本质上，这种方式与 VAE 完全一致，都是最大化观测数据的似然下界

3.8 训练损失的参数化

回顾一下，我们的目标是用神经网络去近似反向扩散过程中的条件概率分布，即：

$p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))$

也就是学一个网络，输入为当前 noisy 的样本 $x_t$ 和步数 t，输出下一个采样点 $x_{t-1}$ 的分布参数（均值与方差）

网络的预测目标（参数化）：我们希望训练神经网络学到 μθ 去预测 $\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)$ ，这相当于用网络去逼近理论上最优的逆向均值。但由于 $\mathbf{x}_t$ 在训练时是已知输入，且 $\epsilon_t$ （加的噪声）也已知，所以我们可以对高斯噪声项重新参数化，改为让网络从时间步 t 的输入 $\mathbf{x}_t$ 中预测 $\mathbf{x}_0$ ：

$\begin{aligned} \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\ \text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) \end{aligned}$

即用神经网络预测 $\epsilon_\theta(x_t, t)$ （给定当前 noisy 状态和步数），然后根据公式还原回 $\mu_\theta(x_t, t)$ 。这样做的好处就是模型预测的是高斯噪声项，容易拟合，也和 VAE 里的 reparameterization trick 很像

损失项 $L_{t-1}$ 被参数化为：神经网络预测的 $\mu_\theta$ 与理论上真实的 $\tilde{\mu}_t$ 的差异，用均方误差最小化二者差距：

$\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}$

a. 此处实际是 KL 散度二次型推导后的标准均方误差表达

b. 展开后带入 $\mu_\theta$ 和 $\tilde{\mu}_t$ 相减消掉，剩下的是预测噪声与真实噪声的差别

c. 最终实际只剩下“预测噪声与真实噪声的均方误差”，且有权重因子

3.9 简化（Simplification）

Ho et al. (2020) 实际经验发现，直接忽略权重项，仅用普通的 MSE 损失，训练效果更好。即直接用预测噪声和真实噪声的均方误差（MSE）做损失，无需加权

$\begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}$

这里的 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon_t$ 是正向扩散采样公式，等价于先加噪声再训练

最终训练目标：

$L_\text{simple} = L_t^\text{simple} + C$

其中 C 是与模型无关的常数项，可以直接忽略

3.10 训练与采样算法流程伪代码

图 4. The training and sampling algorithms in DDPM (Image source: Ho et al. 2020)

1. 训练流程（Algorithm 1）：实际上就是“加噪声-去噪声”配对，拟合真实噪声

1: 从数据分布采样 $x_0$

2: 均匀采样一个步数 t

3: 从标准正态分布采样噪声 $\epsilon$

4: 构造噪声样本 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$

5: 用网络预测噪声 $\epsilon_\theta(x_t, t)$

6: 计算损失 $\|\epsilon - \epsilon_\theta(x_t, t)\|^2$ ，反向传播更新参数

2. 采样流程（Algorithm 2）：相当于从纯噪声逐步“去噪”，生成最终的高质量数据样本

1: 采样最终噪声 $x_T \sim \mathcal{N}(0, I)$

2: 逐步从 t=T 到1：

若 t>1，采样标准正态噪声 z
计算 $\epsilon_\theta(x_t, t)$
按公式 $x_{t-1} = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t, t)) + \sigma_t z$ 生成下一个 $x_{t-1}$