微积分知识点回顾与总结(七):多元微分
- 1.偏导数
- 2.多元复合函数求导
- 3.隐函数求导
- 4.几何应用
- 4.1空间曲线
- 4.2空间曲面
- 4.3方向导数
- 4.4梯度
- 5.代数应用
- 5.1无条件极值
- 5.2条件极值
我们这里所说的多元,做题中只涉及到二元的情况。
注意:在求(x,y)=(1,1)这点的极限时,分别对x->1和y->1求lim值,求出的lim值相等表明极限存在,不等表示不存在。折合一元情况一样:极限存在且唯一存在。
关于连续函数,某点极限值=函数值,则连续,与一元情况一样。
关于多元函数在有界闭区域上的性质:最值定理、有界定理、介值定理,也与一元一样。
1.偏导数:

混合偏导数:
若函数连续,则:
全微分:


多元复合函数求导:
1.

2.


3.隐函数求导:
一个约束条件的情况很容易做。
两个约束条件下:
情形一:



情形二:



4.几何应用:
4.1空间曲线:
1.


2.
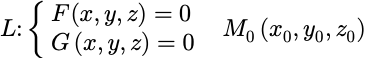


4.2空间曲面:

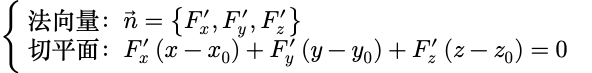
4.3方向导数:
在这里插入图片描述


4.4梯度:

5.代数应用:
5.1无条件极值:
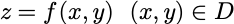
第一步:

第二步:



5.2条件极值:
(一)

第一步:

第二步:

把求出的所有(x,y)代入z=f(x,y),比较选择出极大值和极小值。
(二):

第一步:
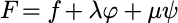
第二步:

把求出的所有(x,y,z)代入z=f(x,y,z),比较选择出极大值和极小值。
























 1960
1960

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








