Soft MoE

本文提出了一种可微的稀疏混合专家 Transformer 模型 (fully-differentiable sparse Transformer) Soft MoE 来解决端到端训练困难的问题，同时也能够保持 MoE 方法的优势，即以较低的推理成本更大的模型容量。 

Soft MoE 提出了一种新的可微稀疏混合专家模型，稀疏混合专家 (Sparse Mixture of Experts, MoE) 是一种在保证模型训练和推理的成本不显著增加的情况下，大幅度提升模型容量的方法。

MoE 方法已经有很长的一段历史了，是一种扩大模型容量的经典高效的做法，但是它的缺点是：

1. 训练不稳定

2. Token Dropping 的问题

3. 较难扩展 Expert 的数量

4. 低效率的微调

造成以上问题的一个原因是 MoE 的端到端训练困难，因此，本文提出了一种可微的稀疏混合专家 Transformer 模型 (fully-differentiable sparse Transformer) Soft MoE 来解决端到端训练困难的问题，同时也能够保持 MoE 方法的优势，即以较低的推理成本更大的模型容量。Soft MoE 的特点是给每个专家输入不同 token 的权重混合。

视觉实验结果证明，Soft MoE 大大优于标准 ViT 和流行的 MoE 方法，比如 128 个 Expert，16 个 MoE 层的 Soft MoE-Huge/14 模型参数比 ViT-Huge/14 多 40 倍，但推理时间成本仅增长 2%，同时性能要好得多。

1 Soft MoE：一种完全可微的稀疏 Transformer

论文名称： From Sparse to Soft Mixtures of Experts

论文地址： https://arxiv.org/pdf/2308.00951.pdf

• 1 Soft MoE 论文解读：

1.1 背景：把离散优化问题变为可微的优化问题

稀疏混合专家 (Sparse Mixture of Experts, MoE) 是一种在保证模型训练和推理的成本不显著增加的情况下，大幅度提升模型容量的方法。在视觉，语言和多模态任务中都取得了成功，代表像视觉的 V-MoE[1]，文本的 Switch Transformer[2]和多模态的 LIMoE[3]。

如下图1左所示，稀疏 MoE Transformer 的核心是一个离散优化问题，即：模型需要决定每个输入 token 应该输入哪些 Expert 里面，这些 Expert 一般是 MLP 模块。输入 token 和 Expert 之间的匹配 (token-to-expert match) 是 MoE 中要考虑的很重要的问题之一，之前也有各种各样的方法尝试解决此问题，比如基于线性规划的[4]，比如基于 RL 算法的[5]，比如基于固定规则的[6]，比如基于最优传输理论的[7]，和基于贪婪匹配的[8]。总之，解决好稀疏 MoE 的这个离散优化问题的确是件不容易的事情。稀疏 MoE 的缺点有：

1. 训练不稳定

2. Token Dropping 的问题

3. 较难扩展 Expert 的数量

4. 低效率的微调

图1：Sparse MoE 和 Soft MoE 的区别：左：Sparse MoE，给每个 Expert 分配一定的输入 token。右：Soft MoE，给每个 Expert 分配的是所有输入 token 的加权平均值

如下图1右所示，Soft MoE 把稀疏 MoE Transformer 的这个离散优化问题变成了可微的优化问题。Soft MoE 觉得不必一定要 "hard" 地找到输入 token 和 Expert 之间的一一匹配，而是可以 "Soft" 地混合输入 token 并且分给每一个 Expert。Soft MoE 给每个 Expert 分配的不是某几个输入 token，而是所有输入 token 的加权平均值 (权重取决于 token 和 Expert)，然后由这个对应的 Expert 去处理这个加权平均值。

1.2 变为可微的优化问题之后，解决了之前稀疏 MoE 的什么问题？

问题1： 精心设计的 Expert-to-token 的路由机制通常并不比随机固定路由好。

Soft MoE 可以避免这个问题，因为每个路由的参数都是基于每个输入 token 直接更新的。

问题2： 训练不稳定 (LIMoE[3]这个工作观察到在训练期间，可能有大部分 token 改变路由，给训练带来一定挑战) 导致很多稀疏 MoE 方法的 Expert 都不可以设置得很多。

Soft MoE 可以避免这个问题，扩展到数千个 Expert。

1.3 Soft MoE 算法描述

参数配置：

整个过程如下图2所示。

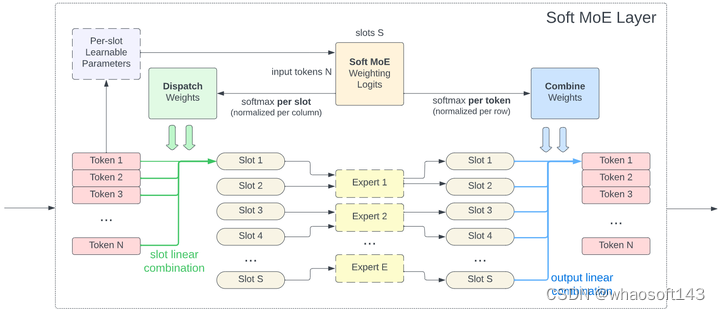
图2：Soft MoE 算法流程图

遵循稀疏 MoE 的常用设计思想，作者用 Soft MoE 块替换了 Transformer 的一部分 MoE 块。slot 的总数是 Soft MoE 的关键超参数，因为时间复杂度取决于 slot 的数量，而不是 Expert 的数量。比如，可以设置等于输入序列长度的 slot 数以匹配等效密集 Transformer 的 FLOP。

Soft MoE 的 JAX 代码：

def soft_moe_layer(X, Phi, experts):
    # Compute the dispatch and combine weights.
    logits = jnp.einsum('md,dnp->mnp', X, Phi)
    D = jax.nn.softmax(logits, axis=(0,))
    C = jax.nn.softmax(logits, axis=(1, 2))
    # The input slots are a weighted average of all the input tokens,
    # given by the dispatch weights.
    Xs = jnp.einsum('md,mnp->npd', X, D)
    # Apply the corresponding expert function to each input slot.
    Ys = jnp.stack([
    f_i(Xs[i, :, :]) for i, f_i in enumerate(experts)],
    axis=0)
    # The output tokens are a weighted average of all the output slots,
    # given by the combine weights.
    Y = jnp.einsum('npd,mnp->md', Ys, C)
    return Y

全部代码：

https://github.com/google-research/vmoegithub.com/google-research/vmoe

1.4 Soft MoE 的一些关键性质

1) 完全可微：

Sparse MoE 算法的通病是 token 和 Expert 之间存在的分配问题，有时精心设计的 Expert-to-token 的路由机制通常并不比随机固定路由好。输入 token 和 Expert 之间的匹配 (token-to-expert match) 是 MoE 中要考虑的很重要的问题之一，之前也有各种各样的方法尝试解决此问题，比如基于线性规划的[4]，比如基于 RL 算法的[5]，比如基于固定规则的[6]，比如基于最优传输理论的[7]，和基于贪婪匹配的[8][9]。所有这些方法本质上都是离散，不可微的。

Soft MoE 可以避免这个问题，因为每个路由的参数都是基于每个输入 token 直接更新的。

2) 可以避免掉 Token Dropping 和 Expert Unbalance 的问题

MoE 算法里面每个 Expert 都会处理一些 token，很自然地就会带来 Token Dropping (有的 token 不会分配给任何一个 Expert) 和 Expert Unbalance (一些 Expert 会比另一些 Expert 分配到更多 token) 的问题。

Soft MoE 可以避免这个问题，因为每个 slot 的输入都是所有 token 的加权平均值。

3) 运算速度快

Soft MoE 的主要优点是完全避免了之前算法中的 token 排序或 top-k 操作，因为这些操作的速度慢，而且不太适合硬件加速器。因此，Soft MoE 明显快于大多数 Sparse MoE 算法。

4) Soft MoE 算法是密集的 MoE 算法还是稀疏的 MoE 算法？

要回答这个问题我们需要首先搞明白为什么 Sparse MoE 算法是稀疏的。Sparse MoE 是稀疏的这件事的根本原因是每个 Expert 的输入特征仅仅是一部分的 token，而 Soft MoE 的输入是所有输入 token 的加权平均值，因此不能算作是稀疏的。

Soft MoE 也不能算作是 Dense MoE 算法，因为每个 Expert 仅仅会处理输入 token 的子集。

5) Soft MoE 算法需要归一化

Transformers 中，MoE 层通常用于替换每个编码器块中的 FFN 层，因此如果去遵循大部分 Transformer 架构的 Pre-Normalization 方法，就需要使用归一化，这里 Soft MoE 针对  的操作是：

l2_normalize(X, axis=1)

scale * l2_normalize(Phi, axis=0)

其中，scale 是可学习的参数，l2_normalize 的定义是：

def l2_normalize(x, axis, eps=1e-6):
    norm = jnp.sqrt(jnp.square(x).sum(axis=axis, keepdims=True))
    return x * jnp.reciprocal(norm + eps)

6) Soft MoE 算法和注意力机制 (Multi-Head Self-Attention) 的区别和联系？

1.5 Soft MoE 算法的局限性

• 自回归解码 (Auto-regressive decoding)：

因为 Soft MoE 算法要在运行过程中合并所有的输入 token，因此很难实现自回归。因为自回归必须在训练期间保留过去的 token 和未来 token 之间的因果关系 (Causality)。

Self-Attention 解决这个问题的手段是依赖于注意力的掩码 (Mask) 机制。如果想在 Soft MoE 中实现这一点就需要特别小心 token 之间的依赖和相关关系。总之研究 Soft MoE 算法的自回归解码是个很有价值的方向。

• 内存消耗

Soft MoE 倾向于利用大量 Expert，而其成本和 Dense Backbone 类似，使得模型的内存需求可能变大。

1.6 图像分类实验结果

训练数据集

预训练数据集： JFT-4B：一个私有数据集，其最新版本包含超过 4B 张图像，涵盖超过 29k 个类。预训练的过程中评价指标是 JFT-4B 上的上游验证精度 Precision-at-1 和 ImageNet 10-shot 精度 (冻结模型权重，并用一个新的权重来计算的，该数据集仅在包含来自 ImageNet-1K 的每个类包含 10 张图像的数据集上进行训练)。

微调数据集： ImageNet-1K 训练集。

验证集： ImageNet-1K 验证集。

模型尺寸：

ViT-S/8, ViT-S/16, ViT-S/32, ViT-B/16, ViT-B/32, ViT-L/16, ViT-L/32, ViT-H/14。

方法：

Token Choice, Expert Choice 和本文的 Soft MoE。

训练策略：

300k steps, Batch Size 4096

Pareto Model 实验结果：

如下图3所示是四种方法 Soft MoE, Experts Choice, Tokens Choice, Dense 在预训练过程中的 JFT-4B Precision-at-1 的结果和 ImageNet 10-shot 的精度的训练成本/性能帕累托边界。Soft MoE 算法在这两个指标上都优于之前的方法。

图3：四种方法在预训练过程中的 JFT-4B Precision-at-1 的结果和 ImageNet 10-shot 的精度的训练成本/性能帕累托边界

更长的训练结果：

本文还测试在更长的训练 step 下模型的性能如何，把从 Small 到 Huge 的模型训练了 4K steps，用 128 个 Expert 的 Soft MoE 替换 ViT S/16、B/16、L/16 和 H/14 中的最后一半 Block 中的 FFN，每个 Expert 使用一个 slot。

由于模型并行性所需的额外数据传输，Large Soft MoE 模型产生的 wall-clock time overhead 很小。所有变体都训练了 4M 步，除了 H/14，出于成本原因训练了 2M 步，实验结果如下图4和5所示。

如下图4所示是 Soft MoE 和 ViT 的 JFT-4B 精度、ImageNet 10-shot 精度和 ImageNet 微调精度与 ExaFLOPS 的训练成本。

图4：不同模型更长的训练 step 下的 JFT-4B 精度

如下图5所示是所有结果。对于给定的计算预算，Soft MoE 模型大大优于 Vision Transformer 模型。比如 Soft MoE-S/16 在 JFT-4B 和 ImageNet 10-shot 上的表现优于 ViT-B/16，它还提高了完整 ImageNet 数据的微调分数，即使它的训练 (和推理) 成本要小得多。同样，Soft MoE-B/16 在上游任务 JFT-4B 和 ImageNet 10 shot 的表现优于 ViT-L/16，微调后仅落后 0.5，同时速度快 3 倍，所需的 FLOP 减少了近 4 倍。最后，Soft MoE-L/16 模型优于 Dense H/14 模型，同时在推理速度又快 3 倍左右。

图5：不同模型更长的训练 step 下的实验结果

根据前面的实验结果，较小的 Soft MoE 的性能可以匹配较大的视觉 Transformer，作者因此继续训练小模型 Backbone，希望以非常低的训练成本获得更高质量的模型。

作者观察到对于 Soft MoE 方法而言，较长的 cooldown (学习率线性减小到零的时期) 可以很好地适用于 Soft MoE，因此将 cooldown 从 50k steps 增加到 500k steps。

实验结果如下图6和7所示。Soft MoE-B/16 训练了 1k TPUv3 Days，优于在相似时间预算上训练的 ViT-H/14，而 Soft MoE-B 模型的 FLOPs 要低 10 倍，wall-clock time 低 5.7 倍。即使将 ViT-H/14 的训练代价加倍，Soft MoE-B 模型的性能也可以与之相匹配。Soft MoE-L/16 模型的在推断上比 ViT H/14 快近 2 倍的同时性能大大优于所有模型。

图6：不同训练代价和尺寸的 Soft MoE 模型和 ViT 的 JFT-4B Precision-at-1 性能和 ImageNet 10-shot 性能        whaosoft aiot http://143ai.com

图7：Soft MoE 模型和 ViT 的实验结果

视觉-文本对比学习实验结果

作者还验证了 Soft MoE 得到的模型在其他任务的性能。具体而言作者探索了一种流行的范式，即图像语言对比学习，这里遵循的是 LiT[10] 方法，其中图像塔在图像分类任务上进行了预训练，然后在在图像-文本对数据集上训练文本编码器时冻结。

视觉编码器作者重用了在 JFT 上训练的模型，对比学习在 WebLI 上训练，这是一个专有数据集，由 10B 图像和从互联网上抓取的 ALT 文本组成。图像编码器被冻结，而文本编码器从头开始训练。实验结果如下图8所示，Soft MoE -L/16 在 Imagenet 和 Cifar-100 零样本上的性能分别比 ViT-L/16 高出 1% 和 2% 以上。

图8：对比学习实验结果