图像平滑处理-高斯滤波(一) (Gaussian Filter)

小魔王降临

已于 2022-01-27 10:18:52 修改

阅读量7.6k

点赞数 4

分类专栏： # 【OpenCV_滤波】文章标签： smooth

于 2019-05-28 19:12:19 首次发布

本文链接：https://blog.csdn.net/qq_30460949/article/details/90441267

版权

【OpenCV_滤波】专栏收录该内容

10 篇文章

订阅专栏

本文介绍了高斯滤波，它是一种线性平滑滤波，适用于消除高斯噪声。阐述了其具体操作，还给出C++ API函数及参数解释。分析了一维和二维高斯函数，探讨了sigma值和核大小对图像的影响，如sigma越大图像越模糊等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

高斯滤波(Gauss filter)实质上是一种信号的滤波器，其用途为信号的平滑处理，数字图像用于后期应用，其噪声是最大的问题，因为误差会累计传递等原因，大多图像处理教材会在很早的时候介绍Gauss滤波器，用于得到信噪比SNR较高的图像（反应真实信号）。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。

C++ API函数

void cv::GaussianBlur(InputArray src,
OutputArray dst,
Size ksize,
double sigmaX,
double sigmaY = 0,
int borderType = BORDER_DEFAULT)

参数解释：

InputArray src: 输入图像，图像可以有任意数量的通道，这些通道是独立处理的，图像深度为CV_8U、CV_16U、CV_16S、CV_32F、CV_64F。
OutputArray dst: 输出图像，与输入图像有相同的类型和尺寸。
Size ksize: 高斯内核大小，这个尺寸与前面两个滤波kernel尺寸不同，ksize.width和ksize.height可以不相同但是这两个值必须为正奇数，如果这两个值为0，他们的值将由sigma计算。
double sigmaX: 高斯核函数在X方向上的标准偏差
double sigmaY: 高斯核函数在Y方向上的标准偏差，如果sigmaY是0，则函数会自动将sigmaY的值设置为与sigmaX相同的值，如果sigmaX和sigmaY都是0，这两个值将由ksize.width和ksize.height计算而来。具体可以参考getGaussianKernel()函数查看具体细节。建议将size、sigmaX和sigmaY都指定出来。
int borderType=BORDER_DEFAULT: 推断图像外部像素的某种便捷模式，有默认值BORDER_DEFAULT，如果没有特殊需要不用更改，具体可以参考borderInterpolate()函数

高斯函数

一维高斯函数：
可以看到，G(x)的跟sigma的取值有极大的关系。sigma取值越大，图像越平缓，sigma取值越小，图像越尖锐。

二维高斯函数：
二维高斯是构建高斯滤波器的基础。可以看到，G(x,y)在x轴y轴上的分布是一个突起的帽子的形状。这里的sigma可以看作两个值，一个是x轴上的分量sigmaX，另一个是y轴上的分量sigmaY。对图像处理可以直接使用sigma并对图像的行列操作，也可以用sigmaX对图像的行操作，再用sigmaY对图像的列操作。它们是等价的。
当sigmaX和sigmaY取值越大，整个形状趋近于扁平；当sigmaX和sigmaY取值越小，整个形状越突起。

高斯滤波原理就是将上图的二维正态分布应用在二维的矩阵上，G(x,y)的值就是矩阵上的权值，将得到的权值进行归一化，将权值的范围约束在[0,1]之间，并且所有的值的总和为1。
假设一个3*3的核，sigma取值1.5以及sigma取5.0，归一化后其权值分布分别是：

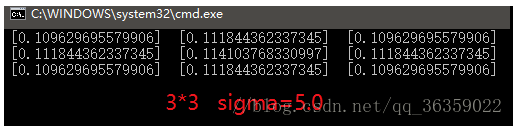
假设一个5*5的核，sigma取值1.5以及sigma取5.0，经归一化后其权值分布分别是：

可以看到，权值的分布是以中间高四周低来分布的。并且距离中心越远，其对中心点的影响就越小，权值也就越小。
因此可以总结：
（1）在核大小固定的情况下，sigma值越大，权值分布越平缓。因此，邻域各个点的值对输出值的影响越大，最终结果造成图像越模糊。
（2）在核大小固定的情况下，sigma值越小，权值分布越突起。因此，邻域各个点的值对输出值的影响越小，图像变化也越小。假如中心点权值为1，其他点权值为0，那么最终结果是图像没有任何变化。
（3）sigma固定时，核越大图像越模糊。
（4）sigma固定时，核越小图像变化越小。

不同sigma对应曲线，可以发现sigma越大，越接近中心点（运用滤波器的像素点）的像素权重越大。一个图像应用一个线性滤波器，相当于将内核移动到图像的每个像素上，并将每个对应像素乘以它对应的权重（这要取决于离被应用像素点的距离），这个运算成为卷积。

参考：

OpenCV高斯滤波器详解及代码实现_青城山小和尚-CSDN博客_opencv高斯滤波函数

图像处理基础(4)：高斯滤波器详解 - Brook_icv - 博客园

opencv图像处理-------高斯滤波_YXR11111的博客-CSDN博客