线性代数的几何意义

直到今天看到这个网页，才看见有人一语道破线性代数的真谛（这也是我终于决定写成此文的直接原因）。我终于找到了我那一个学期企图寻找的东西。就好像把 x 变成 2 x 一样，我们经常需要把 (x, y) 变成 (2 x + y, x - 3 y) 之类的东西，这就叫做线性变换。于是才想到定义矩阵乘法，用于表示一切线性变换。几何上看，把平面上的每个点 (x, y) 都变到 (2 x + y, x - 3 y) 的位置上去，效果就相当于对这个平面进行了一个“线性的拉扯”。

矩阵的乘法，其实就是多个线性变换叠加的效果，它显然满足结合律，但不满足交换律。主对角线全是 1 的矩阵所对应的线性变换其实就是不变的意思，因此它叫做单位矩阵。矩阵 A 乘以矩阵 B 得单位矩阵，就是做完线性变换 A 后再做一次线性变换 B 就又变回去了的意思，难怪我们说矩阵 B 是矩阵 A 的逆矩阵。课本上对行列式的定义千奇百怪，又是什么递归，又是什么逆序对，还编写口诀帮助大家记忆。其实，行列式的真正定义就一句话：每个单位正方形在线性变换之后的面积。因此，单位矩阵的行列式当然就为 1，某行全为 0 的行列式显然为 0 （因为某一维度会被无视掉，线性变换会把整个平面压扁）， |A·B| 显然等于 |A|·|B| 。行列式为 0 ，对应的矩阵当然不可逆，因为这样的线性变换已经把平面压成一条线了，什么都不能把它变回去了。当然，更高阶的矩阵就对应了更高维的空间。一瞬间，所有东西都解释清楚了。

几何意义

线性代数的几何意义矩阵的几何意义矩阵由若干向量组成（可以是有限个，也可以是无限可数个），其形式和数学史赋予它的最自然的几何含义和线性空间有关（向量间的加法以及另一个数集带来的乘法为这个空间赋予了基本结构），这部分内容将在后续更新里单独列出来讲。这里不妨先简单直观一些，要么把矩阵画成几个行向量或列向量，要么画成由向量终点组成的图形，这刚好和当代计算机图形学有联系，例如大家常玩的3D游戏或某些基于矢量绘图引擎的2D游戏，就都是矩阵可视化以及矩阵变换的生动实例。如矩阵 按照列向量可表示为如下图形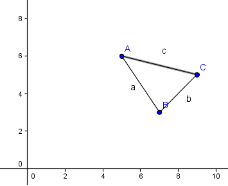
如下图是在matlab中将z=sin(x)*cos(y)算得的离散点组成的矩阵表示成几何图形，当你旋转这个图形观察时，每个画面都是计算机用相应的旋转和投影变换矩阵，对原始的图形数据矩阵相乘变换后得到的，在3D游戏中移动、转动、缩放和光照等也都是靠矩阵运算完成的，当然这里让我们初步感受到一种魔力——矩阵既可以用来表示纯数据（如复杂图形的顶点），也可以用来对数据做变换，在以后的学习中我们会看到，这其实是在说，不仅某阶向量和矩阵全体可以构成一个线性空间，它上面的全体线性变换也构成一个线性空间，即任何线性变换都可以在选择确定的基后，用矩阵来表示。但神奇的东西何止于此，背后还隐藏着更深刻的内容——借用语言哲学的思想，我们对数学语言本身进行反思，会有诸多更本质的东西显现，例如你开始可能会以为离散的加减乘除运算包括矩阵运算等，在工程应用时只能近似和将就，以为偏微分方程等基于连续性的微积分工具才是宝典，但最终会发现，我们所拥有的原子运算只有基础代数运算，而真正"存在"的数学对象都是离散的（连续是一种幻象，或者说只是一个语言概念，而且充当这个语言里的相对本体，可参见奎因哲学），数学世界乃至物理世界都是由离散的对象和它们之间的关系所定义的，这方面有兴趣可以去看看代数几何与前沿物理的思想。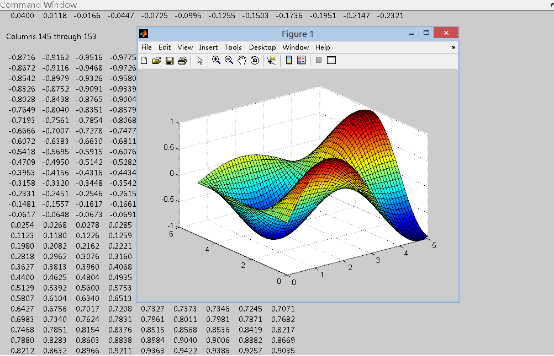
注1：如果单独查看一个矩阵 可以有两种解读：矩阵A由m个n维向量组成，或者由n个m维向量组成；在使用时会根据实际情或约定选择其中一种，而在参与变换或其他运算时，这两种解读一般不能混淆，一定要确定注2：当我们把矩阵表示成图形时，其作图没有固定标准，并不一定是把所有向量终点连接起来构成一个多边形，规则是使用者制定的，可以是网格，可以是离散面片等行列式的几何意义方阵 的行列式的绝对值是其行向量或列向量所张成的平行几何体的空间积，对于二阶行列式，就是向量张成的平行四边形的面积，对于三阶行列式，就是对应平行六面体的体积；如方阵 的行列式绝对值为27，它就是下图平行四边形的面积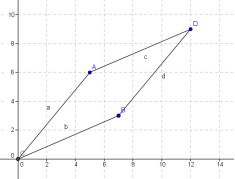注：行列式其实是带有符号的，实际上，正负号表征了这些向量作为线性空间基的手性，正号表示右手系，负号表示左手系，在二阶矩阵的向量空间里，其判别方法是，伸出右手和矩阵的第一个列向量或行向量平行，然后调整手的正反使得能从此向量转过小于180度的角到达第二个向量，这时大拇指如果朝上（从纸面指向自己）则为右手系，矩阵的行列式为正，反之则为左手系，对应行列式为负；如果是三阶矩阵，则从第一个向量转向第二个向量时，如果大拇指指向第三个向量方向（不必重合），则为右手系，其行列式为正，反之为左手系，行列式为负；其实这一点上更广义的表述应是向量空间的基相对自然坐标系的顺序性（代数上可用逆序数表达）克拉默法则的几何意义以二维形式为例来说明其几何意义:现有方程： 其中 ，记 ， 原方程也可表示为 这样可以把 与 看作是列向量 和 的缩放因子，经过伸缩后再叠加即得到和向量 ，故原方程可以解读为把A的列向量缩放并叠加后得到向量 ，求伸缩因子 我们已经知道行列式的几何意义，显然矩阵A对应的平行四边形的面积就是|A|（这里以带符号的有方向面积表示，因为伸缩因子也是有符号的），当某一个向量被伸缩后，如图将OB边伸长至OE，形成新的平行四边形OAFE，记其面积为 这样 的伸缩因子 可表示为 所以只要求出OAFE的面积即可解出未知量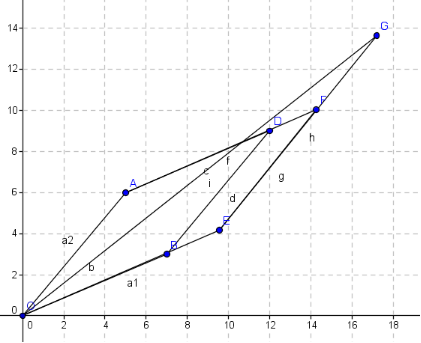
图中OG即向量b，因为它是 的线性叠加，所以G点必在EF的延长线上，这样OG和OE相对OA边的高就是相同的，故OA与OG组成的平行四边形面积和OAFE相同，即所求面积为 ，所以 ，同理可得 矩阵乘法的几何意义我们知道矩阵是由若干向量组成的，因此可自然地把矩阵乘法看作是两个矩阵的同维向量之间做内积（或点乘），而内积的意义是两向量同向投影的乘积，但这只是一个表面的几何含义，比较抽象（也有应用之处，后面会提到）；实际上，对于矩阵乘法C=AB，作用后得到的新矩阵C可以看作是矩阵A经过某种变换得到的，也可以看作是矩阵B经过某种变换后得到的，而这种变换显然就是乘以另一个矩阵的过程，结合前面提到的矩阵的几何意义，故可以把矩阵乘法C=AB看作是图形A（或B）经过变换B（或A）后得到新图形C，或者是向量空间A（或B）经过变换B（或A）后得到新的向量空间C，对于简单的变换矩阵这一点最容易感性体会到；例如变换矩阵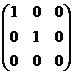
会把原3D图形向x-y面投影，变换矩阵

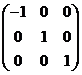
会把原图形对x轴镜像，变换矩阵

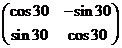
会把原2D图形相对原点逆时针旋转30度。初等变换的几何意义由前面叙述的部分几何意义，我们很快就能看出初等变换的几何含义了交换矩阵的两行（列）：改变向量在矩阵中的排列顺序，当矩阵表示图形时，此操作对图形没有影响，因而矩阵张成的空间维数（秩）不变，但是当矩阵代表向量空间时，会改变此坐标系的手性，当计算方阵的行列式时，会改变其符号；以一个非零数k乘矩阵的某一行（列）：即对矩阵中某一向量进行伸缩变换，整个矩阵代表的图形对应发生变化，由于k不能为0，所以矩阵张成空间的维数（秩）不变，方阵张成的平行几何体的空间积（行列式）变成原来的k倍把矩阵的某一行（列）的k倍加于另一行（列）上：对矩阵中某一向量做线性叠加，且新向量终点总是在另一向量的平行线上，所以对任意矩阵，图形产生了剪切变形，由于剪切变形不会使向量重叠或缩为0，所以张成空间的维数也不变；对于方阵，由前面几何推导克拉默法则的过程知道，如果把某一向量加上矩阵内另一向量的k倍，由于新向量和原向量相对其余向量组成的平行体的高不变，所以方阵对应的平行几何体的空间积不变（行列式不变），例如在matlab中用矩阵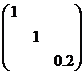作用下面左图对应的矩阵（第三行乘以0.2，即缩短z方向坐标5倍），得到的新图形如下右图所示

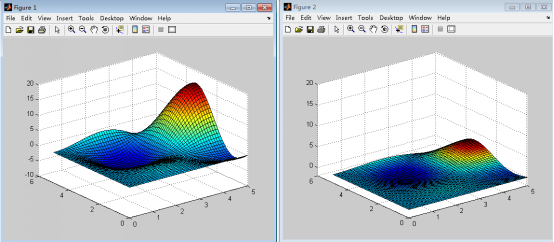
Matlab程序如下，可以动手试一试，还可修改其中的变换矩阵以得到不同效果x=0:0.1:5;y=x;[x y]=meshgrid(x,y); %构造网格z=sin(x).cos(y).x.y; surf(x,y,z); %绘制原图形x=reshape(x,2601,1);y=reshape(y,2601,1);z=reshape(z,2601,1);m=[x y z]; %几何图形对应的n3矩阵t=[1 0 0;0 1 0;0 0 0.2]; %变换矩阵m=mt; %进行变换x=m(:,1);y=m(:,2);z=m(:,3);x=reshape(x,51,51);y=reshape(y,51,51);z=reshape(z,51,51);figure;surf(x,y,z) %绘制变换后的图形然后我们把变换矩阵修改为

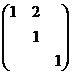
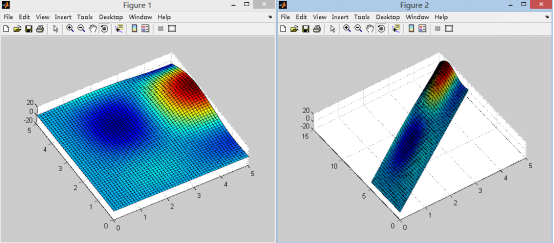
即把第二行乘以2加到第一行，由上述分析知道这样会把原图形沿y方向剪切变形，剪切量为对应x坐标的二倍，实际效果如下图所示，这里我们取俯视角以观察x-y面的情形，从右图可以看出理论分析是正确的（注意观察变换前后的y向坐标值）

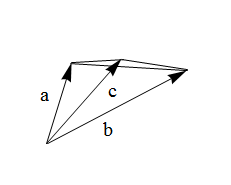
矩阵秩的几何意义矩阵的秩即矩阵的各向量所张成空间的维数不能说秩是矩阵对应图形的维数，因为矩阵的图形只取了各向量的终点，而不含有这些向量的之间的几何关系，故二者的维数不一定相等，而矩阵的秩按定义应取其向量空间维数。如下图中的空间向量a,b,c可以张成一个三维空间，故矩阵(a b c)的秩为3，但是其终点组成的图形是一平面，维数为2，显然和秩是不一样的

结合上面对初等变换的几何解释，正是因为三种初等变换都不改变矩阵向量空间的维数，所以对于复杂的难以观察维数的矩阵，我们可以先用初等变换作用于矩阵进行简化，然后到容易观察的形式时求出它的秩；向量组线性相关/无关的几何意义注：在讨论向量张成的空间相关问题时，某种程度上我们可以把向量组和矩阵等价对待，二者都是一组向量的集合，只是向量组相对矩阵明确了向量的维数与向量个数，而矩阵有行与列两种选择，所以只要确定矩阵的向量取行还是列，就可以把矩阵当作向量组讨论；线性相关在代数上就是一组向量中至少有一个向量能用其余向量线性表示，而几何意义是它们所张成的向量空间维数少于这些向量的个数，这样就至少存在一个向量落在其余向量形成的向量空间中，而向量空间实际上是一个坐标系统，所以处于其中的点（向量）都可以由这些向量定位出来（线性表示），在向量之间表现出一种相关性；而线性无关的几何意义就是一组向量张成空间的维数等于这些向量的个数，这样没有任何一个向量落在其余向量形成的空间里，每一个向量对其余向量来说都是超越自身空间维度的（独立的），因而无法被定位（线性表示），表现成一种相互无关性

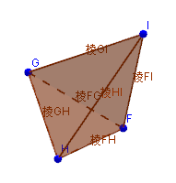
以上图棱锥为例，因为HI处于GH和GI所形成的面里，所以HI必然可以由这两个向量表示，所以三者线性相关（三者形成的空间维数为2<3）；而HI在IG和IF形成的平面之外，所以H点无论如何都不能被GI和IF定位到，同时IF也不在IG和HI形成的平面里，IG不在IH和IF形成的平面里，同理可知它们之间不能线性表示，所以三者线性无关（三者形成的空间维数为3=向量个数）方程Ax=0的几何意义由前面叙述容易看出此方程表示向量x与A的每一个行向量都垂直，或者说向量x垂直于矩阵A的行向量空间。这样我们可以直接根据几何意义得到结论：Ax=0有非零解的充要条件是矩阵A的秩要小于x的维数n；这是因为对于确定维度的向量空间M，如果我们可以找出独立于它的一维或多维空间N，则在空间N里的向量总是垂直于空间M；例如在直角坐标系O-xyz中，设A是x-y平面上的向量空间，x是空间向量，因为z维上的向量总是垂直于A，所以x在这一方向上存在无数非零解。反之若矩阵A的秩等于n，且x非零，则由于x也在n维空间内，所以它和A中的行向量必然线性相关，无法独立于A的行向量空间，所以这时仅有零解。当方程有非零解时，设A的向量空间维数为R（秩），由上叙述可知解向量x中存在n-R个分量取值自由，如果我们把这n-R个自由变量看作是一个n-R维空间中的向量坐标时，显然此空间中每一个向量都能确定原方程组的一个解，又因为每一个向量都可以用这个n-R维空间的一组单位正交基线性表示，所以这组单位正交向量所确定的一组解通过线性组合就可以表示出原方程的任意解，故这组解就是原方程的一个基础解系，上述叙述也正是基础解系的几何意义方程Ax=b的几何意义设A是mn矩阵，x是n维向量，由前述几何意义知道，如果b处于A的向量空间中（b和A的向量线性相关），则一定可以由A的向量线性表示，也即解存在，而b落在A的向量空间等价于b的维数小于等于向量空间A的维数，也可表述为R(A)=R(A b)=R，即A的秩等于增广矩阵的秩，这种表达也是许多教科书中常用的。当R=n时，n维向量x的每个分量都是线性表示的确定系数，故只有唯一解，而R<n时，向量空间有n-R个维度不存在，故这些维度上对应的系数可任意（自由变量），这时存在无穷多解