[NeurlPS 2022] STaR: Self-Taught Reasoner Bootstrapping Reasoning With Reasoning

• NeurlPS 2022，CCF-A，NLP 顶会
• 有可能是 GPT o1 背后的技术之一，因此重新引起关注；
• 开源代码：https://github.com/ezelikman/STaR

本文的想法是一种简洁的美。LLM 论文不一定需要花里胡哨的数学公式。

翻译说明：

• rationales：本文翻译为“理由”，这里大概含义是答案的思考过程/做题思路。
• rationalization：文本翻译为“合理化”

【UPD：2024/12/08】增加了对 STaR 开源代码的解读：[NeurlPS 2022] STaR 开源代码实现解读

文章相关知识

• 离散隐变量：离散隐变量模型是一种统计模型，它假设观测数据是由一些未观测到的（隐含的）变量决定的。在这种情况下，离散意味着这些隐变量的值是可以从有限集合中选取的。例如，在自然语言处理中，一个离散隐变量模型可能用来预测一个词给定上下文的概率，其中隐变量可以是词的潜在语义类别。

• GPT-J：GPT-J 是一个基于 GPT-3，由 60 亿个参数组成的自然语言处理 AI 模型。该模型在一个 800GB 的开源文本数据集上进行训练，并且能够与类似规模的 GPT-3 模型相媲美。

• 数据集：

  • CommonsenseQA （CQA）
  • Grade School Math (GSM8K)

几个细节

Q1：微调后，STaR 是否也需要回答之前迭代中正确回答的问题？
A1：需要

Q2：STaR 微调后是否有可能导致之前回答正确的问题，现在回答不正确了？
A2：如Fig.5，里面是震荡上升，说明存在这种情况。

Q3：合理化让模型强行给出解释，如果模型还是回答不对，这个数据是否会被用于微调？
A3：不会

Q4: 合理化是否会引入偏见？
A4: 参考fig4，不合理化虽然慢，但慢工出细活、大器晚成（但训练代价大），合理化后，上限低于前着（但学的更快）

Q5:本文设置的温度，贪婪解码的次数对STaR方法的影响是什么？
A5:

---

正文

Abstract

生成逐步的“思维链”理由(rationales)能够提高语言模型在复杂推理任务上的表现，比如数学或常识问答。然而，目前诱导语言模型生成理由要么需要构建庞大的理由数据集，要么只能通过少量样本推理牺牲准确性。我们提出了一种技术，通过迭代利用少量理由示例和一个没有理由的大型数据集，来引导模型逐渐掌握更复杂的推理能力。这项技术，名为“自我教学推理器”（STaR），依赖于一个简单的循环：生成理由以回答许多问题，提示一些理由示例；如果生成的答案是错误的，尝试在给定正确答案的情况下再次生成理由；对所有最终得出正确答案的理由进行微调；重复这个过程。我们展示了 STaR 在多个数据集上的性能显著提高，与直接微调以预测最终答案的模型相比，并且在CommensenseQA 上的表现与微调一个 30 倍大的最新语言模型相当。因此，STaR 让模型通过学习自己生成的理由来提升自己。

1 Introduction

人类决策往往是一系列思考的结果[1, 2]。最近的工作表明，明确的中间推理（“理由”）也能提高大型语言模型（LLM）的性能[3-8]。例如，[5]展示了LLMs明确训练使用“草稿本”进行中间步骤可以在算术上达到完美的分布内性能，并且在分布外泛化方面表现强劲，而直接训练预测答案的模型则无法做到这两点。这些工作表明，在给出最终答案之前生成明确的“理由”对LLMs在多种任务上是有价值的，包括数学推理、常识推理、代码评估、社会偏见推断和自然语言推理。然而，诱导理由生成的两种主要方法都有严重的缺点。

一种理由生成的方法是构建一个理由的微调数据集，无论是由人工注释者手动完成，还是通过手工制作的模板自动完成[3-5, 9]。手动方法成本高昂，并且为每个有趣的问题构建这样的数据集是不切实际的[3]。同时，基于模板的方法依赖于自动生成的理由，但这只在一个通用解决方案已经知道[5]或者可以制定合理的硬编码启发式方法时才有效[4]。

另一种选择是利用上下文学习（in-context learning），通过在语言模型提示中只包含少量理由示例来实现。这已被证明可以相对于没有理由的提示（“直接”提示）提高数学和符号推理任务的准确性[5, 6]。然而，尽管带有理由的少量样本技术往往胜过不带的方案，它们通常大大逊色于使用大型数据集微调模型直接预测的答案[5, 6]。

在这篇论文中，我们采取了不同的方法：通过利用大型语言模型（LLM）的现有推理能力，我们迭代地引导模型生成高质量的理由。 具体来说，我们通过少量样本提示一个大型语言模型来自我生成理由，并通过微调那些导致正确答案的理由来进一步提炼模型的能力。我们重复这个过程，每次都使用改进后的模型来生成下一组训练数据。这是一个协同过程，其中理由生成的改进提高了训练数据的质量，而训练数据的改进又进一步改进了理由生成。

然而，我们发现这个循环最终无法解决训练集中的任何新问题，因为它没有直接的训练信号来解决它未能解决的问题。为了克服这个问题，我们提出了合理化：对于模型未能正确回答的每个问题，我们通过提供正确的答案来生成一个新的理由。这允许模型反向推理——已知正确答案，模型可以更容易地生成一个有用的理由。然后，这些理由被收集为训练数据的一部分，这通常可以提高整体准确性。

因此，我们开发了自我教学推理器（STaR，见图1）方法，这是一种可自我扩展的(scalable bootstrapping)方法，允许模型学习生成自己的理由，同时也学习解决越来越困难的问题。在我们的方法中，我们重复以下过程：在每次迭代中，首先尝试使用当前模型的理由生成能力来构建一个微调数据集；然后，使用合理化来增强这个数据集，为模型未能解决的问题的理由提供依据；最后，在合并的数据集上微调大型语言模型。

将 STaR 应用于算术、数学应用题和常识推理，我们观察到它能够有效地将少量的少量样本提示转化为大型理由数据集，从而显著提高性能。在常识问答（CommonsenseQA）[10]上，我们发现STaR 在性能上超过了few-shot baseline（+35.9%）和直接微调以预测答案的 baseline（+12.5%），并且与一个 30 倍大的微调模型表现相当（72.5% vs 73.0%）。

因此，我们做出以下贡献：

1. 我们提出了一种 bootstrapping 机制，可以从少量初始示例中迭代生成理由数据集，而无需检查新理由的正确性。
2. 我们将理由生成与合理化相结合，其中模型被赋予解释答案的任务，然后像它在没有任何提示的情况下提出理由一样进行微调。我们展示了合理化加速并改进了 bootstrapping 过程。
3. 我们在数学和常识推理领域使用多种消融技术评估了这些技术。
4. 据我们所知，我们提出了第一种技术，允许预训练的大型语言模型迭代地使用其语言建模能力来提升自身。

2 Background and Related Work

上下文学习 最近，一系列研究工作探讨了大型语言模型进行上下文学习的能力[11, 12]。本质上，上下文学习将少量样本学习视为一个语言建模问题，通过在上下文（即提示）中展示几个示例，并允许模型学习和识别应用于新示例的模式。一些研究基于贝叶斯推断从语言建模目标出发研究上下文学习[13]，而另一些研究则尝试从“induction heads”的角度 mechanistically 地描述这一过程[14]。此外，提示配置的差异已被证明对少量样本性能有显著影响。一些人甚至发现，用可以在嵌入空间中优化的“软提示”替换少量样本提示可以获得显著提升[15]。与强调问题的表现不同，我们关注的是模型的输出；特别是，我们关注的是模型在得出结论之前对问题进行推理的能力。

理由 关于理由对语言模型性能影响的初步工作是[3]，该研究表明在数据集上训练语言模型，使其在答案前明确展示理由，可以提高模型生成最终答案的能力。然而，这需要成千上万的训练示例由人工注释者手动标注人类推理。最近，[5]展示了逐步的“草稿本”可以提高在算术、多项式求值和程序评估等任务上微调的大型语言模型（LLM）的性能和泛化能力。类似地，[6]使用单个少量样本“思维链”推理提示来提高模型在一系列任务上的性能，而无需微调。最后，[16]表明，如果满足以下条件，课程学习方法可以帮助解决形式数学问题：1）它们被翻译成Lean（一种定理证明语言[17]），2）可以直接评估证明的有效性，3）可以为每个问题采样许多潜在的解决方案，4）训练了一个单独的值函数模型，5）从GPT-f（一个已经微调在大型数学数据集上的模型[18]）开始。我们注意到，在许多领域并非所有这些条件都适用。此外，一些工作旨在解释为什么理由有这种有益的效果：一些人从潜在变量模型的角度分析了它们的影响[19]，而其他人则提供了中间任务监督益处的正式证明[20]。

迭代学习 提出了多种迭代学习算法，其中找到的解决方案或成功的方法反过来被用来找到更多的解决方案[21, 22, 16]。[21]引入了专家迭代（ExIt），这是一种强化学习技术，也是我们方法的灵感来源。本质上，它由“学徒”的 self-play 循环组成，随后是来自是 slower “专家”的模仿学习以及反馈，然后将专家替换为现在改进的学徒。[16]在ExIt的基础上进行形式推理，而[22]将迭代学习应用于使用可以组合成模块化网络的视觉问答。STaR和专家迭代方法[21]之间有进一步的相似之处。例如，基于最终答案是否与目标匹配来过滤生成的示例可以被视为专家反馈。然而，我们有一个固定的“专家”，并且不训练一个单独的值函数。

自然语言解释 从可解释机器学习的角度讨论自然语言解释，重点在于解释而不是推理[23, 24]。这一工作线的动机主要基于可解释的决策制定，类似于[3]，普遍没有发现要求事后解释可以提高模型性能。

3 Method

3.1 Rationale Generation Bootstrapping (STaR Without Rationalization)

我们有一个预训练的大型语言模型M和一个包含问题x和答案y的初始数据集：$D=\{(x_i,y_i){\}}_i^D=1$。我们的技术从一个小的提示集 P 开始，其中包含带有中间理由的示例：$P=\{(x_{p_i},r_{p_i},y_{p_i}){\}}_i^D$ (P<<D, eg. P=10)。像标准的少量样本提示一样，我们将这个提示集连接到D中的每个示例上，即：$P=\{(x_{p_1},r_{p_1},y_{p_1}),\dots \dots ,x_{p_P},r_{p_P},y_{p_P},x_i)\}$。这鼓励模型为$x_i$生成理由$\widehat{r_i}$，接着是答案$\widehat{y_i}$。我们假设导致正确答案的理由比那些导致错误答案的理由质量更高。因此，我们过滤生成的理由，只包括那些结果为正确答案的理由 $\widehat{y_i}=y_i$。我们在过滤后的数据集上微调基础模型 M，然后通过使用新微调的模型生成新的理由来重启这个过程。我们不断重复这个过程，直到性能趋于稳定。在这个过程，一旦我们收集了一个新的数据集，我们就从原始预训练的模型 M 开始训练，而不是持续训练一个模型以避免过拟合。我们在算法1中提供了这个算法的概要。
STaR可以被视为一个类似于RL风格的策略梯度目标的近似。可以看到，M 可以被视为一个离散隐变量模型$p_M(y|x)={\sum }_{r}p(r|x)p(y|x,r)$换句话说，M 在预测 y 之前先采样一个潜在的理由 r。现在，给定指示奖励函数$1(\hat{y}=y)$，整个数据集的总预期奖励是：

$$\begin{gathered} J(M,X,Y)=\sum _i{E}_{{\hat{r}}_i,{\hat{y}}_i\sim p_M(\cdot |x_i)}[1({\hat{y}}_i=y_i)], \\ \nabla J(M,X,Y)=\sum _i{E}_{{\hat{r}}_i,{\hat{y}}_i\sim p_M(\cdot |x_i)}[1({\hat{y}}_i=y_i)\cdot \nabla \log p_M({\hat{y}}_i,{\hat{r}}_i|x_i)]; \end{gathered}$$

其中梯度是通过策略梯度的标准对数导数技巧获得的。注意，指示函数丢弃了所有未导致正确答案 $y_i$ 的的采样理由的梯度：这是STaR中的过滤过程（第5行）。因此，STaR通过（1）贪婪解码样本$(\widehat{r_i},\widehat{y_i})$来减少这个估计的方差（以可能的有偏探索理由为代价），以及（2）在同一批数据上采取多次梯度步骤(类似于一些策略梯度算法[25])。来近似$J$。这些近似使得 STaR 成为一个简单且广泛适用的方法，可以使用标准的 LLM 训练机制来实现；未来的工作应该更密切地研究 STaR 和上述 RL 目标之间的联系。

这里有两个关键点，1）贪婪解码，由于指示函数会丢弃一些结果，如果只给出一次(r,y)输出，可能会漏掉回答正确的case（LLM计算能答对这个题，也不一定能每次都答对），r是隐变量（有多种可能性），加上LLM本身也有随机性，每次输出的r可能不同，所以广泛多次尝试然后选择正确回答的来使用会好一些。但这个过程是有偏的，因为无法穷尽所有的r空间，但是这种做法对模型性能有提升，所以可以接受。2）里公式的概率是标准方法，理论可以参考策略梯度相关文章。这里也不用深究1）2），后面算法伪代码不涉及这些。

3.2 Rationalization

rationale generation bootstrapping 算法存在一个限制。由于模型仅在它正确回答的样本上进行训练，当模型无法解决训练集中的新问题时，改进就会停止。这是因为该算法无法从失败的样本中获得任何训练信号。受[3]的启发，我们提出了一种我们称之为“合理化”的技术。具体来说，我们向模型提供答案作为提示，并要求它以与先前理由生成步骤相同的风格生成理由。给出答案，模型能够反向推理，因此更容易生成导致正确答案的理由。例如，在图2中，我们提供了提示，即“(b) 购物车”是正确答案，以生成理由。我们对模型未能通过理由生成解决的问题应用合理化。在将 rationalization-generated rationale 添加到我们的数据集中时，我们不会在相应的提示中包含 hint，就好像模型在没有任何提示的情况下想出了理由一样。过滤后，我们在先前生成的数据集和合理化生成的数据集上进行微调。

算法1描述了完整的算法，其中蓝色部分对应于合理化。没有这些部分，算法1对应于无合理化的STaR。图1提供了一个概述图。在合理化生成的数据集上进行微调有一个关键好处，即让模型接触到它原本不成功的难题。这可以被理解为挑战模型"think outside the box"思考它未能解决的问题。合理化的次要好处是增加了数据集的大小。

4 Experiments

为了我们的实验，我们专注于算术、常识推理和小学数学，以展示STaR的广度。特别是，对于算术，我们遵循了[5]中的设置。对于常识问答，我们遵循[13, 6]并使用CommonsenseQA（CQA），这是一个广泛使用的多项选择数据集，用于此领域[10]。对于小学数学，我们使用[9]中的GSM8K。

4.1 Experimental Protocol

我们使用GPT-J作为我们的基线语言模型，并使用GPT-J存储库[26]中的微调脚本。我们选择GPT-J，这是一个6B参数模型，因为检查点和微调代码是公开可用的[26]，并且该模型足够大，可以生成非平凡的理由以从中bootstrap。更多关于GPT-J和我们微调的超参数细节包含在附录H中。按照[26]的默认设置，我们执行100步的学习率预热，从这一点开始我们使用恒定的学习率。除非另有说明，我们通常第一个外循环的训练40步，并在每个外循环中增加20%的微调训练步骤。总的来说，我们发现在开始时更慢地训练最终有利于模型性能。我们期望通过彻底的超参数搜索可能会有进一步的改进——由于计算限制，我们将其留作未来的工作。

对于算术问题，我们首先生成一个包含50,000个随机抽样问题的算术数据集（均匀分布在数字长度上），基于[5]中的描述。对于算术的每个外循环迭代，我们从数据集中抽取10,000个问题。我们使用不同位数的10个随机 few-shot rationale examples 作为其相应的 few-shot prompt。对于CommonsenseQA 训练集中的 9,741 个问题，我们将每个问题添加到 few-shot rationale prompt 中，并提示模型为该问题生成理由和答案。对于 CQA 的 few shot prompting，我们从[6]中使用的10个问题开始，理由稍作修改以修正错误答案，并更明确地引用相关知识。我们在附录B1中包含了这些修改后的提示。这些提示构成了我们的完整解释集。我们运行STaR直到看到性能饱和，并报告最佳结果。

在执行合理化时，我们发现在第一个迭代之后，在后续的外循环迭代中包含或省略少量样本提示对方法的最终性能没有实质性影响。然而，有一些细微差别我们在第5节中进一步讨论，导致我们通常建议使用 few-shot prompt，除非另有说明。

4.2 Datasets

算术 算术任务是计算两个n位整数的和。我们根据[5]中的描述生成数据集，并在图3中可视化一个示例草稿本。直到包括“Target：”在内的一切都是作为提示给出的，模型被要求生成草稿本（由“<scratch>”标记开始/结束）和最终答案，如[5]所述。草稿本的每一行对应于从最后一个数字到第一个数字的每对数字的求和，累积最终数字的答案，以及一个进位数字，表示前一对数字的和是否至少为10。我们包括1到5位数字的少量样本提示。在执行合理化时，我们在“Target：”之后包含正确答案，并查询模型以产生草稿本，然后在草稿本之后生成正确答案。

CommonsenseQA 多项选择常识推理任务，CommonsenseQA [10]（CQA），是从ConceptNet 构建的，这是一个包含超过一百万节点的概念及其关系的语义图[28]。[10]在ConceptNet中为每个问题识别了一组“target”概念，其中目标概念与一个“source
”概念共享语义关系。然后每个问题都是众包的，允许读者在提到源概念的同时识别一个目标概念。此外，还添加了两个干扰项。数据集包含12,247个问题，每个问题有五个选项，其中9,741个在训练集中，1,221个在开发集中，1,285个在（保留的）测试集中。
对应于ConceptNet的广泛多样性，CQA包含了一系列多样化的问题，这些问题需要建立在标准世界知识基础上的常识推理能力，其中人类的表现是89%[10]。许多人指出CQA包含许多偏见，包括性别[3]。我们在附录G中讨论了这可能如何影响我们的方法。还存在许多错别字和本质上含糊不清的问题。尽管存在这些问题，我们还是使用它，因为它是一个依赖于共同世界知识和简单推理的一般性问答数据集，这为我们的方法提供了一个很好的测试平台。

Grade School Math (GSM8K) 我们还在GSM8K数据集上进行评估，该数据集包含7,473个训练和1,319个测试的小学级数学问题[9]。这些数学问题以自然语言提出，并需要两到八步计算才能得出最终答案。这个数据集结合了算术和常识推理所需的技能。

4.3 Symbolic Reasoning: Results on Arithmetic

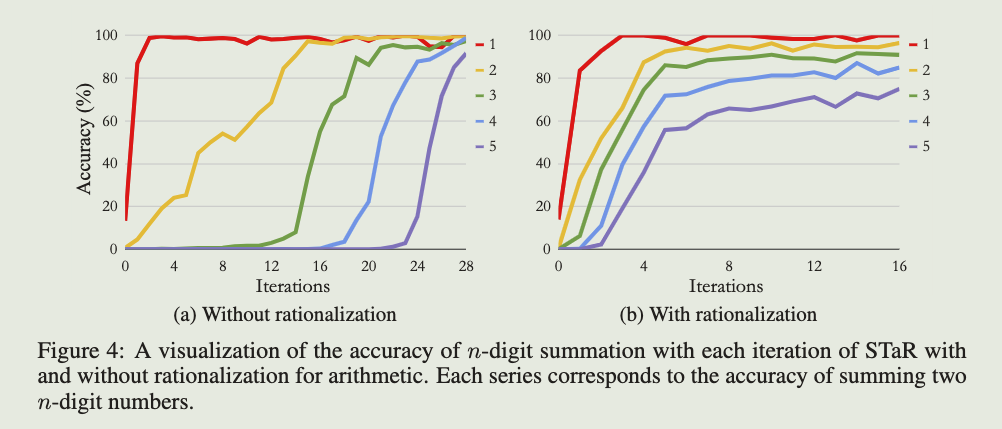
图4中绘制了模型在1-5位数字上的准确性，分别对应于外循环的每次迭代。在运行16次迭代的STaR后，总体准确率达到89.5%。作为参考，一个在10,000个示例上训练而没有 rationales 的baseline，在5,000步后达到76.3%的准确率。值得注意的是，即使有 rationales，算术问题的 few-shot 准确性非常低：2位加法的准确性不到1%，而更多位数的准确性接近零。

有了合理化，准确性能够特别迅速地提高。在对模型生成的草稿本进行一次微调迭代后，2位加法的准确率从不到1%提高到32%。如果没有合理化，性能改进是阶段性的：模型通常在对(n-1)位数字求和表现良好之前，对n位数字求和的表现都很差。有了合理化，模型可以同时学习许多长度，尽管准确率并不相同。合理化允许许多问题可以通过 few-shot 解决，因此我们从300步开始STaR训练（注意，没有合理化这样做会导致在1位加法上过拟合），并且每次迭代增加20步训练。

我们还在第20次迭代开始继续对STaR进行预训练，增加额外的数字位数，同时保持每次迭代的总训练样本数量固定。我们发现，这不仅能够迅速提高对初始数字集的性能，而且在评估从未在训练中见过的9位和10位数字示例时，模型成功解决了许多这些分布外问题。如图5所示，引入这些数字似乎使训练变得不那么稳定，但确切原因尚不清楚。

4.4 Natural Language Reasoning: Commonsense Question Answering

常识问答（CQA）设置引入了几个新挑战。在算术任务中，推理步骤中的一个错误草稿，非常可能导致错误的答案。另一方面，CQA问题是5选1的多项选择题。因此，无论推理的质量如何，随机选择正确答案的概率大约是20%。此外，一些简单的启发式方法（例如语义相似性）可以在没有任何推理的情况下将这个概率显著提高到约30%，如[10]所示。

我们按照实验协议评估这个数据集，并与几个基线方法进行比较。第一个基线是直接对GPT-J进行微调以输出最终答案，我们称之为“GPT-J微调”。我们还与[29]中直接预测最终答案的GPT-3微调基线，以及[6]中使用思维链（CoT）理由提示的137B参数Lambda模型进行了比较。

我们发现，如表1所示，没有合理化的STaR超过了直接在整个数据集上对最终答案进行微调的GPT-J，尽管训练的数据更少。包含合理化的性能提高到了72.5%，非常接近30倍大的GPT-3的73%。正如预期，我们还看到STaR超过了几个样本基线，包括更大得多的137B LaMDA模型[30, 6]。我们预计，如果我们对具有更高样本性能的模型应用STaR，准确率会进一步提高。

注意：这个标里的细节。文字部分说“Note the final STaR model is trained on 78.2% of the training dataset with rationale generation, and an additional 8.5% from rationalization”，而表格里不带合理化的STaR准确率只有68.8%，这里78.2%和68.8%有个差值！这里要怎么理解：因为带有合理化后，fine tune，导致模型处理hard问题的能力提升，所以在之后的实验中，部分问题不需要合理化就可以解出，所以涨了近10个点。

但这里还有一个统计问题，因为这个是不断迭代的，每次都会重新回答，上一次问题A没回答对，用了合理化回答对了，微调后，不需要合理化也能答对，那对这个样本是算合理化的样本还是算什么？这里涨的点是指的，用了合理化也没答对，但是微调后，能答对的样本吗？（因为这种样本没有靠合理化来答对，所以不算入合理化的统计数字里？），论文这个地方的数据，没有写太清楚！这个地方读者如果有研究可以评论区讨论～

案例研究 评估理由的质量更加困难：对于算术，可以与真实的理由进行比较，但对于CQA，评估必然是定性的。因此，我们在图7中包括了一个案例研究。我们观察到，提供的理由通常是合理的，并且与少量样本理由的结构相似。我们得出以下两个观察结果：
1.在使用STaR训练后，我们看到模型能够为新问题生成合理的论据，这解释了观察到的性能提升的一部分。
2.我们还看到，在许多情况下，STaR提高了相比于 few-shot 中的示例的理由质量。

人类评估 基于STaR可能即使在通过 few-shot 提示后最初就能正确回答问题时也能提高理由质量的观察，我们进行了初步的定性分析。我们随机选择了50个由 few-shot CoT和STaR生成的理由，这些问题它们都正确回答了，以及[3]中人类为这些问题生成的理由。然后我们将这些问题和理由的随机子集呈现给20名Prolific[31]上的众包工作者，理由以随机顺序呈现，要求他们根据哪个理由最能证明答案，对理由进行排名。参与者更倾向于将STaR生成的理由排在少量样本理由之前的可能性高30%（p = .039）。这表明，如案例研究所提到的，STaR可以提高理由生成的质量。

我们还发现，参与者更倾向于选择 STaR 生成的理由而不是人类生成的理由的可能性高74%（p < .001）。需要澄清的是，我们不认为这表明人类级别的理由生成性能。相反，我们认为这表明引出高质量理由的困难性。我们在附录C中复制了测试提示，并详细讨论了众包解释数据集的局限性。

失败案例 最后，我们发现了许多有趣的失败案例，其中许多对应于标准逻辑谬误。例如，模型经常做出与问题主题相关的陈述，但这些陈述实际上并不是为什么答案应该是真的论据。有时，模型声称问题意味着答案作为论据，而没有解释为什么。其他时候，特别是在训练初期，模型回答时好像它对某个特定个体有所了解，而不是做出一般性的陈述——例如，“国王的城堡是他感到安全的地方”，而不是“城堡是国王感到安全的地方”。我们在附录A中提供示例并分析错误。

Few-shot prompt trainning 在微调过程中包含少量样本提示[12]似乎带来了显著的性能提升（无合理化时从60.9%提高到68.8%，合理化后从69.9%提高到72.5%）。因此，我们通常建议至少在训练的某一部分中使用它，尽管我们在第5节中讨论了一些注意事项。

4.5 Mathematical Reasoning in Language: Grade School Math

我们再次发现，在GSM8K数据集上，STaR大幅提高了性能，超越了只有理由的 few-shot 或训练去直接预测答案（没有理由），如表2所示，并包括了附录I中的 few-shot 提示。我们观察到，在这个任务上，合理化并没有显著提高性能。注意，在训练中，为了防止训练过程变得不切实际地长，我们有必要在第30次迭代后（经过7912步后）限制训练步骤的数量。目前的结果来自于 STaR 无合理化方法的36次迭代，而合理化额外增加了10次迭代。

大多数情况下，模型生成的计算步骤数量与人类采取的步骤数量相匹配（通常在所有迭代中达成53%至57%的一致性）。我们在图6中明确地可视化了这一点。我们看到，当真实情况和模型在计算步骤数量上不一致时，模型通常使用的步骤更少。有时这是因为模型跳过了步骤，但有时它找到了不同的解决方案。我们在附录J中展示了一个例子，其中模型忽略了多余的信息，并将一个7步的问题简化为一步解决。

5 Discussion and Challenges

合理化的影响 一个关键问题是合理化究竟扮演了什么角色。直观上，合理化允许模型逆向工程一个解决方案，或者提供了一个启发式方法来识别每一步是否使结论更有可能。这与现实世界中的问题相似，其中最终结果已知，但难以推导出一个好的理由。从数学角度来看，虽然理由生成从我们的模型M提供的分布p(r|x)中进行理由采样。合理化条件于答案，让我们可以访问一个替代的分布p(r|x,y)，这可能是一个更好的理由搜索空间。然后合理化可以被看作是一个方程（1）中的 off-policy 目标估计，sampling from the hint-augmented model as a proposal distribution。未来的工作应该建立更多合理化和这些RL目标之间的联系，并更一般地检查合理化何时以及为什么可以改善学习。
此外，由于低采样温度，没有合理化的输出对应于模型对其答案最有信心的例子。这导致这些例子至少在第一次迭代中提供了比合理化例子更弱的梯度信号。由于我们每次运行微调迭代时都从初始预训练模型重新开始训练，这种效果的程度也很难直接测量。最后，我们必须指出，添加“hint”的方法并不直接来自问题和答案，在某些情况下提供它可能是非平凡的【意思是，直接hint还不够，不足以让模型理解问题背后的逻辑】。探索不同 hinting 技术和它们的一般性的各种影响是未来工作的一个途径。
温度 一个直观的替代合理化的方法，如果一个人想要扩展训练数据集，通过更多和更高温度的采样。然而，在实践中，我们发现这是适得其反的。一般来说，它大大增加了尽管推理错误但正确答案的可能性，并且在错误或无关的推理上训练会阻止泛化。这在更结构化的任务中尤其明显，比如算术，其中模型用更高温度的采样方法学会产生的草稿本变得毫无意义，导致模型停滞不前。总的来说，我们发现高温度作为合理化的替代品（例如0.5或0.7）一贯导致比单独使用推理的模型更差。此外，由于大型语言模型的文本生成是顺序的（即不产生前一个标记就无法产生一个标记），生成文本是一个瓶颈，这在计算上远不如合理化高效。例如，生成10个样本输出大约比生成一个样本输出慢10倍。然而，利用多个样本的一个潜在有价值的方法可能是使用[32]中提出的方法，使用多个高温度草稿本的多数票结果作为与低温草稿本比较的真值。这可能允许在只有问题的数据集上应用STaR，而不需要答案。

少样本提示 值得注意的现象是，在采样中包含少量样本提示似乎显著减少了“漂移”，即后来的理由与初始少量样本集的理由越来越不相似。这样做的一个好处是，模型可能不受初始理由的质量和难度的限制，理论上允许它泛化更多。一个潜在的负面后果是，理由的风格可能与原始提示风格匹配得不那么紧密。另一个好处是在计算资源方面——较短的提示长度允许在采样时使用较短的序列长度。技术上，我们在训练时“禁用”少量样本提示的点是另一个可以调整的超参数，但我们将这留作未来的工作。此外，通过在初始外循环迭代后省略提示，模型在训练更长一段时间后进行合理化时表现会逐渐变差。因此，可能需要在长时间训练这种方法时在训练中包含一些提示。

最终，是否在训练的后续迭代中包含少量样本提示的选择似乎取决于用例：当目标是一致地遵循特定的提示风格，这可能有益于可解释性时，包括少量样本提示；当目标是更快的训练循环时，可以移除它们。此外，有可能在其他数据集或更大的模型中，性能会受到这种选择的影响，所以我们鼓励通常将其视为一个超参数。

6 Conclusion

我们介绍了自我教学推理器（STaR），它通过迭代改进模型生成理由以解决问题的能力。我们通过few-shot 提示模型以 step-by-step 的方式解决许多问题，然后提示它为它回答错误的问题合理化正确答案。我们在最初正确的解决方案和合理化的解决方案上进行微调，并重复这个过程。我们发现这种技术显著提高了模型在符号推理和自然语言推理上的泛化性能。

STaR有几个重要的限制。为了使STaR的第一次迭代成功，few-shot 性能必须高于随机选择，这意味着初始模型必须足够大，具有一定的推理能力。例如，我们发现GPT-2甚至无法从算术领域的少量样本推理中引导。另一个限制是，在偶然性能水平很高的情况下（例如二元决策）会产生许多糟糕的理由，这使得STaR方法变得混乱。一个未解决的问题是如何在这些设置中过滤掉糟糕的推理。

尽管如此，我们认为使用没有理由的例子来引导推理是一个非常通用的方法，STaR可以作为许多领域更复杂技术的基石。

Appendix

推荐进一步阅读：[32] Xuezhi Wang, Jason Wei, Dale Schuurmans, Quoc Le, Ed Chi, and Denny Zhou. Selfconsistency improves chain of thought reasoning in language models, 2022.