本人学习隐马尔可夫模型,整理并分享到博客来大家一起共同学习,讨论!
隐马尔可夫模型可以从下面三个方面来学习:
一、基本知识:什么是隐马尔可夫模型
二、理论推导:三个问题——评估问题,学习问题,预测问题以及各自的解决算法/推导
三、实际应用:拓展
1. 基本知识
1.1 是什么模型?
HMM是一个生成模型、概率模型、时序模型、预测模型。
HMM一般被分类到监督学习,但是我个人认为如果使用极大似然估计学习的HMM才是监督学习,如果用Baum-Welch算法学习的HMM应该是属于非监督学习。个人见解不知是否有误,还请大家指正!
1.2 由什么组成?
HMM通常由五元组λ={N,M,π,A,B}组成,一般也可以写成三元组,另外有一些HMM可能有一些不同,这里仅介绍最简单的离散HMM。

A矩阵:代表 t 时刻处于状态 si ,t+1 时刻转移到状态 sj 的概率;
![]()
B矩阵:代表t 时刻处于状态 sj,被观测到 vk 的概率;
![]()
π向量:代表初始时刻处于各隐藏状态的概率。
![]()
1.3 有什么条件?
HMM满足两个基本假设:
(1) 齐次马尔科夫性假设, 隐马尔可分链t的状态只和t-1状态有关
![]()
(2) 观测独立性假设, 观测只和当前时刻状态有关
![]()
有的论文中提到,HMM由一个隐藏的马尔科夫过程和一个与这个隐藏马尔科夫过程概率相关的并且可以观察到的状态集合组成。简单地说就是隐马尔科夫模型是一条看得见的观测序列和一条看不见的隐藏状态序列。

如图所示,横向是时间轴,假设隐状态有三种可能性ABC,每一个观测结果O都对应一个隐藏的状态,可能是A也可能是B也可能是C,这是我们不知道的。隐藏的状态序列可能如红色箭头连接的结果,也可能是别的结果。
2. 理论推导
三个问题——评估问题,学习问题,预测问题以及各自的解决算法/推导。
如果仅是使用HMM无需推导也可以,只需要知道用了哪些算法。

2.1 评估问题
评估问题 已知模型参数,计算某一给定可观察状态序列的概率P( O | λ )
已知: 模型参数λ,观测序列O
目标: P( O | λ )
方法: 前向算法(Forward Algorithm)
后向算法(Backward Algorithm)

★方法:前向算法(Forward Algorithm)
定义前向算子:
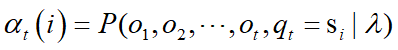
初值:
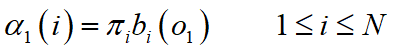
递推:
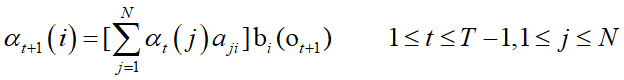
终止:
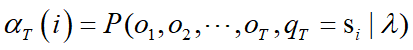
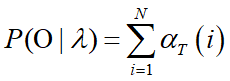
前向算法示意图:
优点:减少计算量的原因在于每一次计算, 直接引用前一个时刻的计算结果, 避免重复计算。
类似的,还有后向算法也可以求评估概率。
★方法:后向算法(Backward Algorithm)
定义后向算子:
![]()
初值:

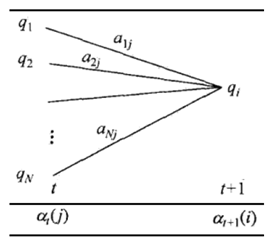
递推:
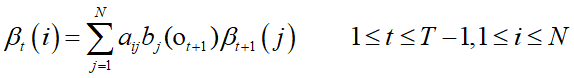
终止:
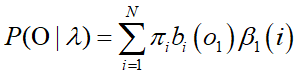
2.1.2 概率计算:这些推导和计算都有大用处!
已知:
![]()
![]()
推导1:
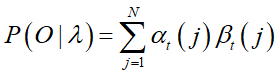

推导2:

这里在推导1的基础上,将后向递推公式代入即可。

推导3:
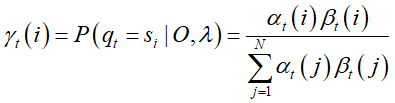
γ 指给定模型 λ 和观测 O,在时刻 t 处于状态 si 的概率。这里用推导1的结果即可。
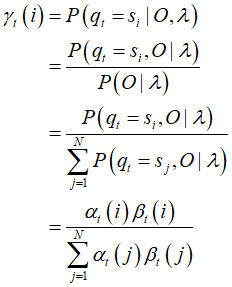
推导4:
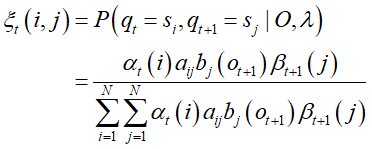
指给定模型 λ 和观测 O,在时刻 t 处于状态 si,时刻 t+1 处于状态 sj 的概率。这里用推导2的结果代入即可。

2.2 解码问题
解码问题
已知模型参数,根据可观察状态的序列找到一个最可能的隐藏状态序列
已知: 模型参数λ,观测序列O
目标: 最可能的隐藏状态序列I
方法: 维特比算法(Viterbi Algorithm)
方法: 近似算法
解码问题简单地说就是去推理得到最可能的那条状态序列。如图所示,通过观测序列O,推测隐藏状态序列,比如红色连接的是最可能的状态序列。

我们只说维特比算法:


★方法:维特比算法(Viterbi Algorithm)
——导入两个变量 δ 和 ψ:
(1)初值.
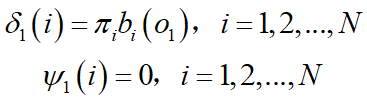
(2)递推. 对 t = 2, 3, … ,
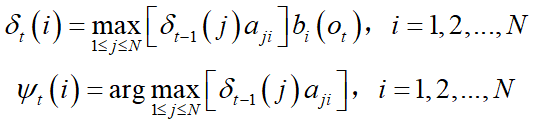
注意:这里和前向算法递推公式的区别:

(3)终止.
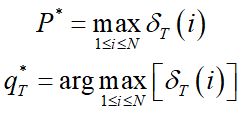
(4)回溯. 对 t = T-1, T-2 , … , 1
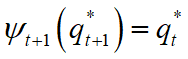
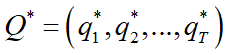
2.2 学习问题
学习问题
根据可观察状态的序列,如何调整模型参数,使得在该模型参数下观测序列O的概率 P(O|λ) 最大?
已知: 观测序列O
目标: 模型参数λ=(A,B,π)
方法: 极大似然估计(监督学习)
Baum-Welch算法(非监督学习)
分段K-均值(Segmental K-means)
我们只学Baum-Welch算法:
训练数据:S个长度为T的观测序列
![]()
训练目标:
![]()
我们将观测序列数据看做观测数据O,状态序列数据看做不可观测的隐数据I,那么隐马尔可夫模型事实上是一个含有隐变量的概率模型

E步

用
![]()
代入得到
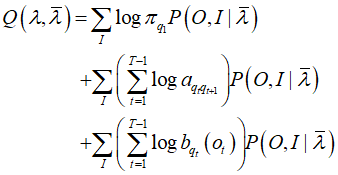
M步
要极大化的参数
![]()
单独出现在3个项,只需分别极大化

对于第一项:
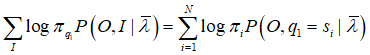
存在约束条件:
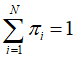
利用拉格朗日乘子法(主要思想是将约束条件函数与原函数联立,从而求出使原函数取得极值的各个变量的解),写出拉格朗日函数:
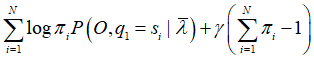
对其求偏导并令结果为0
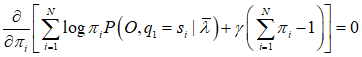
![]()
对 i 求和得到
![]()
代入导函数得到
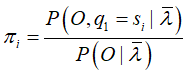
对于第二项:
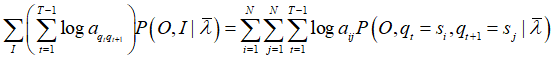
存在约束条件:
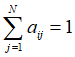
拉格朗日函数
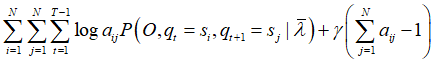
对其求偏导并令结果为0
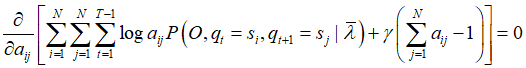
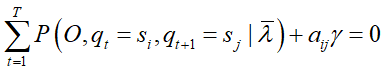
对 j 求和得到
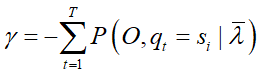
代入导函数得到
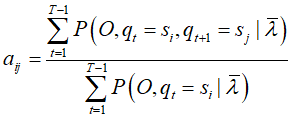
对于第三项:
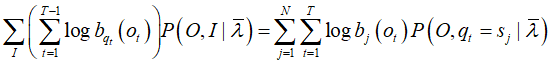
存在约束条件:k是观测值,M是所有观测数
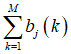
拉格朗日函数
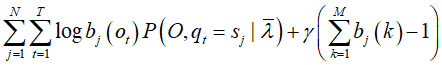
对![]() 求偏导=0,注意,只有在
求偏导=0,注意,只有在![]() 时,
时,![]() 对
对![]() 的偏导数才不为0,用指示函数表示:
的偏导数才不为0,用指示函数表示:![]()
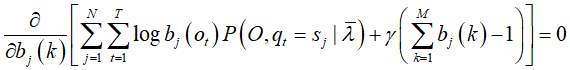
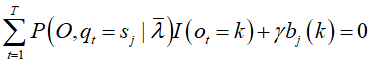
对![]() 求和
求和
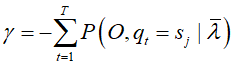
代入导函数得到

推导结束,但这肯定没法直接计算的,所以还要继续推导一丢丢:
将前面评估问题中提到的推导3和推导4代入即可。

得到
![]()

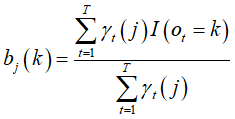
★方法:Baum-Welch算法
输入:观测数据
![]()
输出:模型参数
![]()
(1)初始化:
对于n=0,选取 ![]() ,
,![]() ,
,![]() ,得到初始化模型
,得到初始化模型![]()
(2)递推:对n=1,2,…, 等式右端按 ![]() 计算
计算
![]()
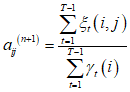
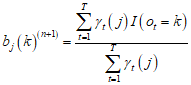
(3)终止:
![]()
终止条件:
1、最大迭代次数 1000次
2、对数似然增益 ![]()
3. 拓展
待续。。。。
参考:《统计学习方法》李航





















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








