CCM DC-DC变换器建模(1)：buck变换器的平均模型和小信号模型

CCM buck变换器的平均模型和交流小信号模型

重新学习了DC-DC建模的方法，类似于平均开关法，记录一下。

顺便考虑一个非理想因素，二极管的压降Vd=0.5 V（假设二极管压降恒定）。使用电路的参数：

平均模型

过程

观察开关M1的电流和Vds波形：

忽略电感电流的波动，可以得到，流过MOS的平均电流 $i_{M1}=D{i}_L$，DS平均电压$v_{DS}=(1-D)(V_i-V_o)$

同样，观察二极管D1的电流和电压波形：

忽略电感电流的波动，可以得到，流过二极管的平均电流 $i_{D1}=(1-D)i_L$，平均反向电压$v_D=D{V}_i-(1-D)V_d$

用受控源来代替开关，可以获得平均模型，总共有四种排列组合：

1. 开关：电压源，二极管：电压源
2. 开关：电压源，二极管：电流源
3. 开关：电流源，二极管：电压源
4. 开关：电流源，二极管：电流源

一般会选择3，开关等效为电流源，二极管等效为电压源，如下图。

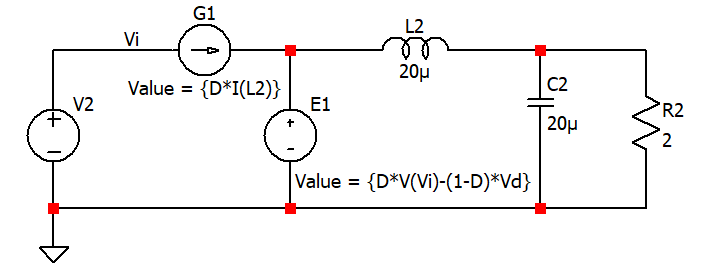
简单验证

左边是buck仿真模型，使用了理想开关。右边是平均模型，开关和二极管用受控源代替。

输入电压跳变时，电感电流和输出电流的波形如下图。可见平均模型和原电路的动态响应波形还是比较接近的。

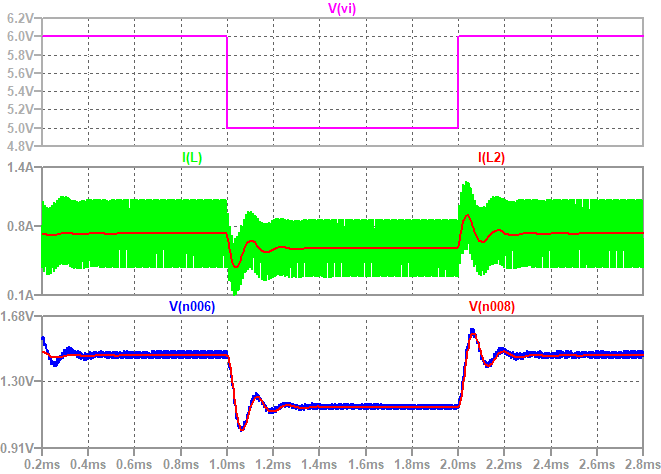
交流小信号模型

过程

因为平均模型中有耦合项，比如开关的电流D*iL，小信号模型是为了获得线性的电路，从而获得传递函数。

建模过程类似于对时间t求全微分
$$\begin{gathered} \Delta (D(t)i_L(t))=D\Delta i_L(t)+D\Delta d(t) \\ \Delta (D(t)V_i(t)-(1-D(t))V_d)=D\Delta V_i+(V_i+V_d)\Delta d(t) \end{gathered}$$
从而受控源都转换成为线性的受控源，如下：

用线性的受控源替换入平均模型，获得交流小信号模型。

• 电感电流平均值IL，用输出电流I(R3)近似代替
• 为了调节占空比d，添加了一个电源V6，用V(d)表示占空比。

简单验证

对比了占空比在0.3和0.4之间跳变的波形。

• 开关电路中，使用PWM调制，调制波幅值5V，因此输入调制器的信号是在1.5V和2V跳变
• 交流小信号模型中，占空比V(d)去除了直流分量，因此是在0V和0.1V跳变。

可以看到交流小信号模型的电感电流和输出电压，相当于把开关电路进行平均后去除了直流偏置。

传递函数

过程

基于交流小信号模型，使用KVL和KCL列写电感电流和电容电压（输出电压）的方程，可以求解传递函数。有空再写。

备注

• 受控源使用了Epoly和Gpoly，使用方法，必须加上 Value=，如Value = {Vi*D}

• 参考视频链接：https://youtu.be/gEyCQSS-sOc