GAMS系列分享6-电力系统最优潮流-3节点最优潮流

最新推荐文章于 2025-03-26 10:46:06 发布

不设闹钟的罗罗

最新推荐文章于 2025-03-26 10:46:06 发布

阅读量6.3k

点赞数 14

分类专栏：电力系统最优潮流直流潮流 GAMS 文章标签：线性代数算法

本文链接：https://blog.csdn.net/qq_34194377/article/details/105302284

版权

本节主要探讨 3节点电力系统

基于直流潮流的

电力系统最优潮流计算。

5.4 关键点：***（对其理解极其重要）

6,一定要背下来的步骤：（几乎所有的程序都是这样）

1，物理模型

2，数学模型

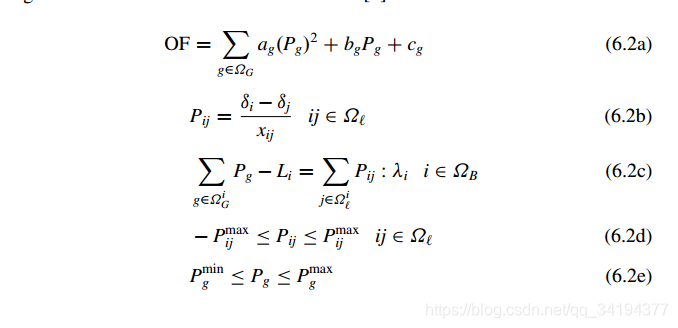
式1，为优化目标

式2，线路直流潮流计算

式3，是各节点功率平衡

式4，线路潮流约束

式5，发电机出力约束

3，程序

* DC-OPF  three-bus network
*集合定义
Sets bus /1*3/,slack(bus) /3/,gen /g1*g2/;
scalars sbase /100/;
alias (bus,node);
*参数设置
Table Gendata(gen,*)
      b     Pmin    Pmax
g1    10    0       65
g2    11    0       100;
set GBconect(bus,gen)
/1  .   g1
 3  .   g2 /;
Table busData(bus,*)
       pd
2      100 ;
set conex
/1  .  2
 2  .  3
 1  .  3/;
 conex(bus,node)$(conex(node,bus))=1;
 Table branch(bus,node,*)
                x        limit
 1  .  2        0.2      50
 2  .  3        0.25     100
 1  .  3        0.4      100 ;
 branch(bus,node,'x')$(branch(bus,node,'x')=0)=branch(node,bus,'x');
 branch(bus,node,'limit')$(branch(bus,node,'limit')=0)=branch(node,bus,'limit');
 branch(bus,node,'bij')$conex(bus,node) = 1/branch(bus,node,'x');

*定义变量
 Variables Pij(bus,node),pg(gen),delta(bus),of;
*方程
 Equations const1,const2,const3;
 const1(bus,node)$conex(bus,node)..pij(bus,node)=e=branch(bus,node,'bij')*(delta(bus)-delta(node));
 const2(bus)..+sum(gen$gbconect(bus,gen),pg(gen))-busdata(bus,'pd')/sbase
                   =e=sum(node$conex(node,bus),pij(bus,node));
 const3..OF=g=sum(gen,pg(gen)*gendata(gen,'b')*sbase);
*模型建立

最低0.47元/天解锁文章