利用超球嵌入来增强对抗训练

利用超球嵌入来增强对抗训练

这次介绍一篇NeurIPS2020的工作，“Boosting Adversarial Training with Hypersphere Embedding”，一作是清华的Tianyu Pang。

该工作主要是引入了一种技术，称之为Hypersphere Embedding，本文将其称作超球嵌入。

该方法和现有的一些对抗训练的变种是正交的，即可以互相融合提升效果。

这里指的对抗训练的变种有 ALP, TRADE 等

对抗训练框架

首先，如下图所示，我们列出来AT以及其变种，用粉色标识出来其训练目标的差异

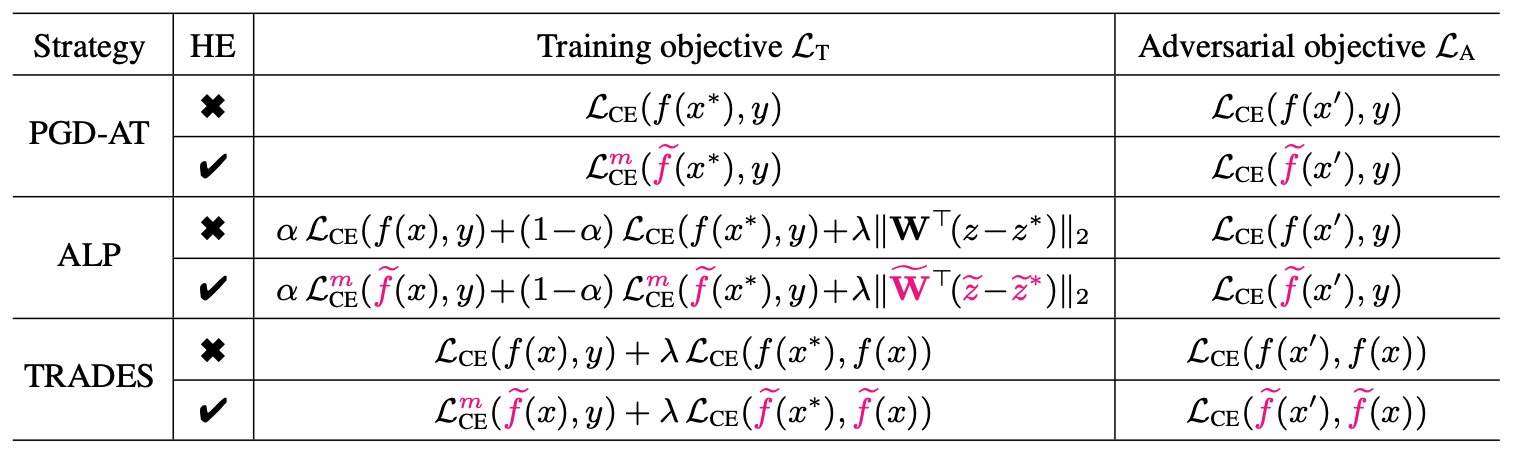
其中，$x^{\ast }$ 是对抗样本，右边的对抗目标可以理解为用于生成对抗样本的误差函数。

我们可以简单地看出来这些变种的设计：

• ALP是加上了正常样本的交叉熵误差，并引入了一个正则化项，$z$ 其实就是$f(x)$
• TRADES则是在引入正常样本的交叉熵误差之后，将原本的对抗样本的误差做了修改，即，从原本的标签 $y$ 改为正常样本的输出 $f(x)$

HE的修改部分主要有两块：

• 在模型 $f$ 上面
• 在交叉熵误差 ${\mathcal{L}}_{CE}$ 上面

方法介绍

记号描述

这里首先给出一些基础的记号，方便后面的描述

我们考虑分类任务，记标签数量为 $L$, 记模型为:
$$f(x)=\mathbb{S}({\mathbf{W}}^{\top }z+b)$$
其中，$z=z(x;\omega )$ 代表着基于模型参数 $\omega$ 抽取出来的特征，矩阵 $\mathbf{W}=(W_1,...,W_L)$ 以及偏置 $b$ 可以理解为最后的线性层，函数 $\mathbb{S}(\cdot )$ 是softmax函数。

我们记交叉熵误差为：
$${\mathcal{L}}_{CE}(f(x),y)=-1_y^{\top }\log f(x)$$
其中，$1_y$ 就是标签 $y$ 的 one-hot 编码，也就是在 $y$ 位置上为1，其余都是0。

我们使用 $\angle (u,v)$ 表示向量 $u$ 和 $v$ 之间的夹角

融合HE的对抗训练框架

首先，大多数的对抗训练可以写成如下的二阶段框架：
$$\underset{\omega ,\mathbf{W}}{\min }\mathbb{E}[{\mathcal{L}}_T(\omega ,\mathbf{W}|x,x^{\ast },y)],\text{where }{x}^{\ast }=\arg \underset{x^{\prime }\in \mathbf{B}(x)}{\max }{\mathcal{L}}_A(x^{\prime }|x,y,\omega ,\mathbf{W})$$
其实就是，先生成对抗样本，然后优化训练目标。

在多次迭代之后，$\mathbf{W}$ 以及 $\omega$ 就会逐渐收敛，为了提高这种对抗训练的性能，有一些工作将metric learning引入进对抗学习之中，不过这些工作的计算代价比较高昂，会导致一些类别偏向，在更强的对抗攻击之下仍然也是脆弱的。

相关材料：

• NeurIPS 2019: Metric learning for adversarial robustness.
• IWSBPR 2015: Deep metric learning using triplet network.
• 更强的对抗攻击：https://github.com/Line290/FeatureAttack

其实这里的motivation并不充分，给的理由仍然不够有力

接下来，直接给出HE的形式，其实就是对特征 $z$ 以及权重 $\mathbf{W}$ 进行标准化
$${\mathbf{W}}^{\top }z=(W_1^{\top }z,W_2^{\top }z,...,W_L^{\top }z)$$
其中 $W_i^{\top }z=\Vert W_i\Vert \Vert z\Vert \cos {\theta }_i$，${\theta }_i=\angle (W_i,z)$

我们令
$$\widetilde{W_i}=\frac{W_i}{\Vert W_i\Vert },\tilde{z}=\frac{z}{\Vert z\Vert }$$
从而有
$$\begin{gathered} \tilde{f}(x)=\mathbb{S}({\tilde{\mathbf{W}}}^{\top }\tilde{z})=\cos \theta \\ \theta =(\cos {\theta }_1,\cos {\theta }_2,...,\cos {\theta }_L) \end{gathered}$$
计算交叉熵函数的时候，引入一个变量 $m$，记：
$${\mathcal{L}}_{CE}^m(\tilde{f}(x),y)=-1_y^{\top }\log (\mathbb{S}(s\cdot (\cos \theta -m\cdot 1_y)))$$
其中 $s>0$ 是一个系数，用于提高训练时候的数值的稳定性

这个 $m$ 的引入是参考了CVPR2018的一篇文章，Cosface: Large margin cosine loss for deep face recognition

理论分析

首先我们定义一个向量函数 ${\mathbb{U}}_p$
$${\mathbb{U}}_p(u)=\arg \underset{\Vert v{\Vert }_p\le 1}{\max }{u}^{\top }v,\text{where }{u}^{\top }{\mathbb{U}}_p(u)=\Vert u{\Vert }_q$$
其中 $\frac{1}{p}+\frac{1}{q}=1$

引理1：给定一个对抗目标误差函数 ${\mathcal{L}}_A$，令 B ( x ) = { x ′ ∣ ∥ x − x ′ ∥ p ≤ ε } \mathbf{B}(x)=\{x'|\Vert x-x'\Vert_p\leq\varepsilon\} B(x)={x′∣∥x−x′∥p​≤ε}，利用一阶泰勒展开，可得 ${\max }_{x^{\prime }\in \mathbf{B}(x)}{\mathcal{L}}_A(x^{\prime })$ 的解为 $x^{\ast }=x+\epsilon {\mathbb{U}}_p({\nabla }_x{\mathcal{L}}_A)$。进一步的，${\mathcal{L}}_A(x^{\ast })={\mathcal{L}}_A(x)+\epsilon \Vert {\nabla }_x{\mathcal{L}}_A(x){\Vert }_q$

证明:

不妨令 $x^{\prime }=x+\epsilon v$，其中 $\Vert v{\Vert }_p\le 1$

从而，${\mathcal{L}}_A(x^{\prime })={\mathcal{L}}_A(x+\epsilon v)$

在 $x=x-\epsilon v$ 处进行泰勒展开，得到 ${\mathcal{L}}_A(x+\epsilon v)\approx {\mathcal{L}}_A(x)+\epsilon v^{\top }({\nabla }_x{\mathcal{L}}_A)$

故 ${\max }_{x^{\prime }\in \mathbf{B}(x)}{\mathcal{L}}_A(x^{\prime })={\mathcal{L}}_A(x)+\epsilon {\max }_{\Vert v{\Vert }_p\le 1}{v}^{\top }{\nabla }_x{\mathcal{L}}_A(x)$

这里需要用到ICML2019 First-order Adversarial Vulnerability of Neural Networks and Input Dimension的一个结 论, 即 ${\max }_{\delta :\Vert \delta {\Vert }_p\le ϵ}|{\partial }_x\mathcal{L}\cdot \delta |=ϵ\Vert {\partial }_x\mathcal{L}{\Vert }_q,\frac{1}{p}+\frac{1}{q}=1$

通过引理1，我们获得了对抗样本 $x^{\prime }$ 对于损失函数 ${\mathcal{L}}_A$ 的影响，同时给出了 $x$ 对 $x^{\prime }$ 的方向。

引理2：令 $W_{ij}=W_i-W_j$ 为两个权重的差值，$z^{\prime }=z(x^{\prime };\omega )$ 为 $x^{\prime }$ 的特征向量，便有
$${\nabla }_{x^{\prime }}{\mathcal{L}}_{CE}(f(x^{\prime }),f(x))=-\sum _{i\ne j}f(x{)}_{i}f(x^{\prime }{)}_j{\nabla }_{x^{\prime }}(W_{ij}^{\top }{z}^{\prime })$$
证明:

$$\begin{array}{rl}-{\nabla }_{x^{\prime }}{\mathcal{L}}_{CE}(f(x^{\prime }),f(x))& ={\nabla }_{x^{\prime }}(f(x{)}^{\top }\log f(x^{\prime }))\\ & =\sum _{i\in [L]}f(x{)}_i{\nabla }_{x^{\prime }}(\log f(x^{\prime }{)}_i)\\ & =\sum _{i\in [L]}f(x{)}_i{\nabla }_{x^{\prime }}(\log [\frac{\exp (W_i^{\top }{z}^{\prime })}{{\sum }_{j\in [L]}\exp (W_j^{\top }{z}^{\prime })}])\\ & =\sum _{i\in [L]}f(x{)}_i{\nabla }_{x^{\prime }}(W_i^{\top }{z}^{\prime }-\log (\sum _{j\in [L]}\exp (W_j^{\top }{z}^{\prime })))\\ & =\sum _{i\in [L]}f(x{)}_i({\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-{\nabla }_{x^{\prime }}\log (\sum _{j\in [L]}\exp (W_j^{\top }{z}^{\prime })))\\ & =\sum _{i\in [L]}f(x{)}_i({\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-\frac{1}{{\sum }_{j\in [L]}\exp (W_j^{\top }{z}^{\prime })}{\nabla }_{x^{\prime }}(\sum _{j\in [L]}\exp (W_j^{\top }{z}^{\prime })))\\ & =\sum _{i\in [L]}f(x{)}_i({\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-\frac{1}{{\sum }_{j\in [L]}\exp (W_j^{\top }{z}^{\prime })}(\sum _{j\in [L]}\exp (W_j^{\top }{z}^{\prime }){\nabla }_{x^{\prime }}(W_j^{\top }{z}^{\prime })))\\ & =\sum _{i\in [L]}f(x{)}_i({\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-\sum _{j\in [L]}f(x^{\prime }{)}_j{\nabla }_{x^{\prime }}(W_j^{\top }{z}^{\prime }))\\ & =\sum _{i\in [L]}f(x{)}_i((1-f(x^{\prime }{)}_i){\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-\sum _{j\ne i}f(x^{\prime }{)}_j{\nabla }_{x^{\prime }}(W_j^{\top }{z}^{\prime }))\\ & =\sum _{i\in [L]}f(x{)}_i((\frac{{\sum }_{i\ne j}\exp (W_j^{\top }{z}^{\prime })}{{\sum }_{t\in [L]}\exp (W_t^{\top }{z}^{\prime })}){\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-\sum _{j\ne i}f(x^{\prime }{)}_j{\nabla }_{x^{\prime }}(W_j^{\top }{z}^{\prime }))\\ & =\sum _{i\in [L]}f(x{)}_i((\frac{{\sum }_{i\ne j}\exp (W_j^{\top }{z}^{\prime })}{{\sum }_{t\in [L]}\exp (W_t^{\top }{z}^{\prime })}){\nabla }_{x^{\prime }}{W}_i^{\top }{z}^{\prime }-\sum _{j\ne i}\frac{\exp (W_j^{\top }{z}^{\prime })}{{\sum }_{t\in [L]}\exp (W_t^{\top }{z}^{\prime })}{\nabla }_{x^{\prime }}(W_j^{\top }{z}^{\prime }))\\ & =\sum _{i\in [L]}f(x{)}_i(\sum _{i\ne j}f(x^{\prime }{)}_j{\nabla }_{x^{\prime }}(W_{ij}^{\top }{z}^{\prime }))\\ & =\sum _{i\ne j}f(x{)}_{i}f(x^{\prime }{)}_j{\nabla }_{x^{\prime }}(W_{ij}^{\top }{z}^{\prime })\end{array}$$

在引理2之上，记 $y^{\ast }$ 是对抗样本 $x^{\ast }$ 的预测输出，其中 $y\ne y^{\ast }$

基于一些先验的观测，通常预测输出标签的概率值（Top1 的概率）要远大于其他标签的概率值

于是有
$${\nabla }_{x^{\prime }}{\mathcal{L}}_{CE}(f(x^{\prime }),f(x))\approx -f(x{)}_{y}f(x^{\prime }{)}_{y^{\ast }}{\nabla }_{x^{\prime }}(W_{y{y}^{\ast }}^{\top }{z}^{\prime })$$
其中 $W_{y{y}^{\ast }}=W_y-W_{y^{\ast }}$

令 ${\theta }_{y{y}^{\ast }}^{\prime }=\angle (W_{y{y}^{\ast }},z^{\prime })$，$W_{y{y}^{\ast }}^{\top }{z}^{\prime }=\Vert W_{y{y}^{\ast }}\Vert \Vert z^{\prime }\Vert \cos ({\theta }_{y{y}^{\ast }}^{\prime })$ 并且 $W_{y{y}^{\ast }}$ 不依赖于 $x^{\prime }$

从而，每次攻击的迭代下， $x$ 的增量为
$${\mathbb{U}}_p[{\nabla }_{x^{\prime }}{\mathcal{L}}_{CE}(f(x^{\prime }),f(x))]\approx -{\mathbb{U}}_p[{\nabla }_{x^{\prime }}(\Vert z^{\prime }\Vert \cos ({\theta }_{y{y}^{\ast }}^{\prime }))]$$
而先前介绍的方法，会使得 $\Vert z^{\prime }\Vert =1$，进而使得攻击的样本更贴近分类边界

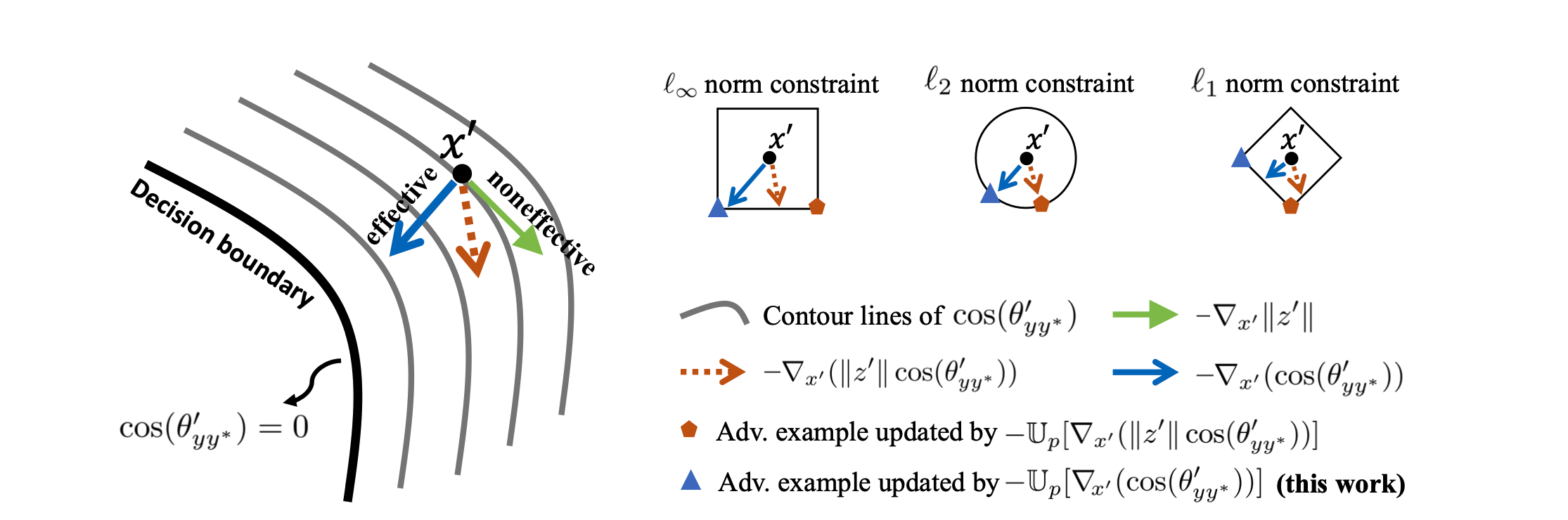
如上图所示，$\Vert z^{\prime }\Vert$ 会影响下降的方向，导致生成的对抗样本产生的作用比较差，进而抑制了对抗训练的效率

实验分析

首先是CIFAR-10上的白盒攻击测试

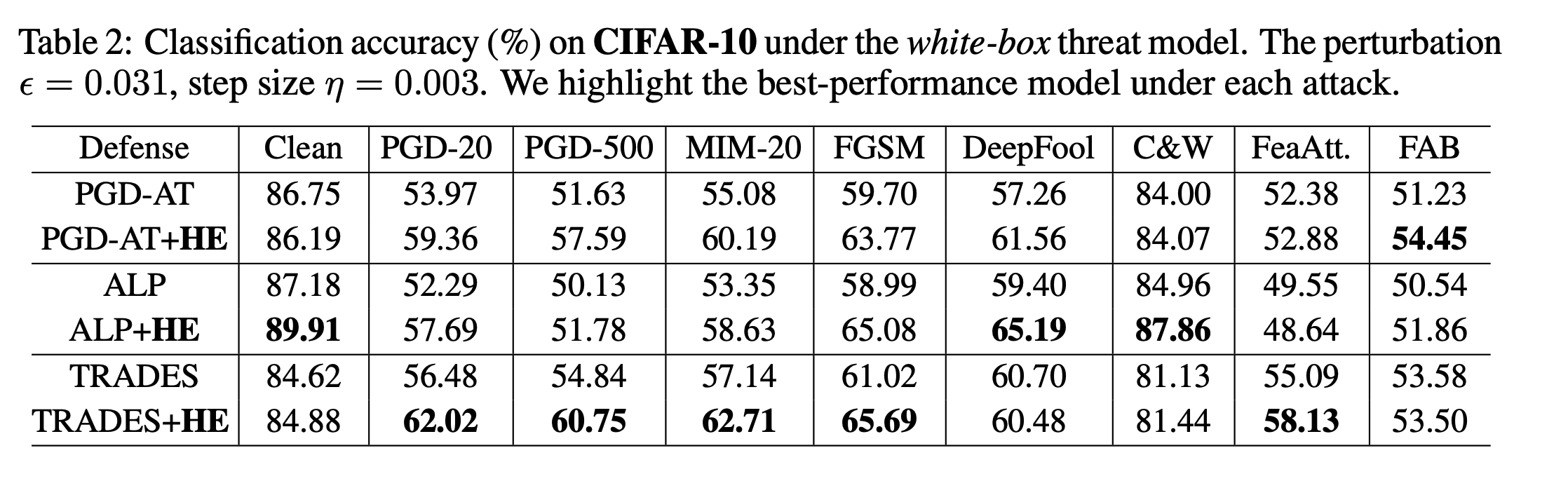
可以看到，加了HE之后防御效果会有一定的提升，少数情况下会下降

然后是ImageNet上的测试

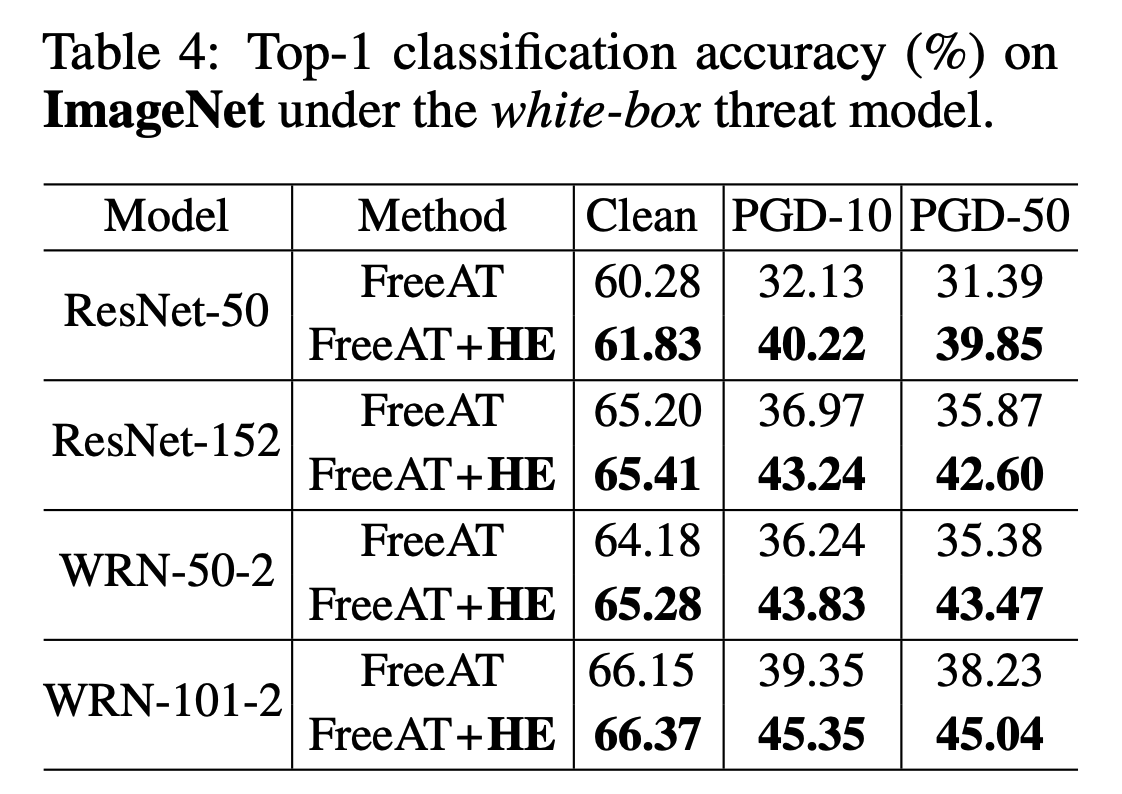
相比FreeAT，防御效果会比较明显