联邦学习下的数据逆向攻击 -- GradInversion

这一次给大家介绍一个攻击，是NVIDIA的一个工作，最近被CVPR2021所收取。

“See through Gradients: Image Batch Recovery via GradInversion”

之所以介绍这个工作，是因为这个攻击通过梯度对于其他人的训练数据进行还原，效果也十分不错。

先前的攻击大多是成员推断攻击（membership inference）, 大家使用差分隐私（DP，Differential Privacy）来进行数据的保护。成员推断攻击的目的是推断一个数据是否被用于模型的训练，但是一般来说大家会假设攻击者手上有一堆数据，既包括训练数据的一部分，也包括一些额外的数据。这个假设还是比较强的，在实际上，攻击者可能根本拿不到训练数据的一部分。

仍然缺少一个比较强的攻击，而这次的工作通过梯度对训练数据进行逆向，结果还十分不错，相当值得分享给大家！

关于联邦学习

首先需要先介绍一下联邦学习，如下图所示：

会有许多参与者一同参与训练过程，每一个参与者拥有自己的数据，并且在本地进行训练，本地训练完之后会上传模型参数，由一个中心节点对进行模型的聚合，然后再下发到每一个参与者本地进行模型的同步。

联邦学习的优势在于，每一个节点的数据都保持在本地，保证了数据隐私，实现了异构数据的访问（也就是每一个参与者自己解决数据的访问问题，即便数据是异构的不会影响整体）。

但是，参与者仍然要将模型上传，这会不会造成数据隐私泄漏呢？

基于梯度的数据还原

首先，我们先给出目标的形式化：
$$x^{\ast }=\arg \underset{\hat{x}}{\min }{\mathcal{L}}_{grad}(\hat{x};W,\Delta W)+{\mathcal{R}}_{aux}(\hat{x})$$
其中 $\hat{x}\in {\mathbb{R}}^{K\times C\times H\times W}$ ($K$ 是batch size, $C,H,W$ 分别是通道数、高度、宽度)， 式子中的 $W$ 是模型的权重，$\Delta W$ 是聚合后的模型权重的变化量。

其中 ${\mathcal{L}}_{grad}$ 的目的是，找到一些可能的输入，使得用这些输入训练后得到的权重，与聚合后的权重尽可能一致。

具体形式为
$${\mathcal{L}}_{grad}(\hat{x};W,\Delta W)={\alpha }_G{\Sigma }_l||{\nabla }_{W^{(l)}}\mathcal{L}(\hat{x},\hat{y})-\Delta W^{(l)}|{|}_2$$
其中 $\Delta W^{(l)}={\nabla }_{W^{(l)}}\mathcal{L}(x^{\ast },y^{\ast })$, 代表真实的训练数据导致的第 $l$ 层权重的变化量

先前的优化式子还有一项，称之为辅助的正则项（auxiliary regularization），具体形式为
$${\mathcal{R}}_{aux}(x)={\mathcal{R}}_{fidelity}(x)+{\mathcal{R}}_{group}(x)$$
由两项组成，第一项驱使 $x$ 与真实的训练样本相似 ，第二项是一致性，我们会在后续给出说明。

批量标签恢复 (Batch Label Restoration)

考虑分类任务，记真实数据为 $x^{\ast }=[x_1,x_2,...,x_K]$ , 对应的标签为 $y^{\ast }=[y_1,y_2,...,y_K]$

对应的真实的梯度为
$${\nabla }_W\mathcal{L}(x^{\ast },y^{\ast })=\frac{1}{K}\sum _k{\nabla }_W\mathcal{L}(x_k,y_k)$$
其中的误差函数可以理解为交叉熵（Cross-Entropy）误差

在分类任务中，网络的最后一层通常是一个全连接的线性层，我们将其记作 $W^{(FC)}\in {\mathbb{R}}^{M\times N}$

其中 $M$ 是输入特征的维数， $N$ 是目标类别的总数目

对于训练样本 $(x_k,y_k)$ 而言，记其线性层的增量为 $\Delta W_{m,n,k}^{(FC)}={\nabla }_{w_{m,n}}\mathcal{L}(x_k,y_k)$

应用链式法则，可以得到：
$$\Delta W_{m,n,k}^{(FC)}={\nabla }_{z_{n,k}}\mathcal{L}(x_k,y_k)\times \frac{\partial z_{n,k}}{\partial w_{m,n}}$$
其中 $z_{n,k}$ 代表输入为 $x_k$ 的最终经过softmax层的第 $n$ 个输出，梯度的形式为
$${\nabla }_{z_{n,k}}\mathcal{L}(x_k,y_k)=p_{k,n}-y_{k,n}$$
也就是对应类别的概率减去标签值

注意到:
$$\frac{\partial z_{n,k}}{\partial w_{m,n}}=o_{m,k}$$
其中 $o_{m,k}$ 就是全链接层的第 $m$ 个输入。

这里需要解释一下，因为 $W^{(FC)}\in {\mathbb{R}}^{M\times N}$ ，其输入为一个 $M$ 维向量 $v\in {\mathbb{R}}^M$

对于一个特定的类别 $n$ , 其输出为 $z_n=v\cdot W[:,n]={\sum }_{i=1}^M{v}_i{w}_{i,n}$

那么，立即有 $\frac{\partial z_{n,k}}{\partial w_{m,n}}=\frac{\partial {\sum }_{i=1}^M{v}_i{w}_{i,n}}{\partial w_{m,n}}=v_m$

$v_m$ 也就是 $o_{m,k}$

由于线性层的输入，通常都是经过ReLU或者sigmoid的激活，所以一般都是非负的，

那么，先前的全连接层的参数的增量 $\Delta W_{m,n,k}^{(FC)}={\nabla }_{z_{n,k}}\mathcal{L}(x_k,y_k)\times \frac{\partial z_{n,k}}{\partial w_{m,n}}$ ，其中的 ${\nabla }_{z_{n,k}}\mathcal{L}(x_k,y_k)$ 这一部分，当且仅当 $n=n_k^{\ast }$ (也就是对应正确的类别时) 这一部分为负。

于是，针对输入 $x_k$ , 我们可以通过上述变化量的符号来判别目标类别，记
$$S_{n,k}=\sum _m\Delta W_{m,n,k}^{(FC)}=\sum _m{\nabla }_{z_{n,k}}\mathcal{L}(x_k,y_k)\times o_{m,k}$$
一旦 $S_{n,k}<0$ , 便意味着 $x_k$ 的类别是 $n$

不过，上述这一切都是基于单个输入 $x_k$ 的，针对 $K$ 个输入，我们有
$$s_n=\frac{1}{K}\sum _k{S}_{n,k}=\sum _m(\frac{1}{K}\sum _k\Delta W_{m,n,k}^{(FC)})$$
这样便产生了一个问题：平均之后的增量，信息出现了丢失，该如何推断类别呢？

这个工作有一个发现，即
$$|S_{n_k^{\ast },k}|\gg |S_{n\ne n_k^{\ast },k}|$$
这意味着，标签的显著性还是比较高的，我们还是可以通过其绝对值来推断，并且，多个样本的梯度聚合之后，负的部分仍然是负的，显现出原始标签的信息。

为了使得这种负号的标志更为鲁棒，文章使用了逐列的最小值，而不是按照特征维度进行求和

即
$$\hat{y}=\arg \text{sort}(\underset{m}{\min }{\nabla }_{W_{m,n}^{(FC)}}\mathcal{L}(x^{\ast },y^{\ast }))[:K]$$
我们来解释上面这个式子，首先注意到 ${\nabla }_{W_{m,n}^{(FC)}}\mathcal{L}(x^{\ast },y^{\ast })\in {\mathbb{R}}^{M\times N}$ 是一个 $M\times N$ 的矩阵

$\min {\nabla }_{W_{m,n}^{(FC)}}\mathcal{L}(x^{\ast },y^{\ast })$ 也就是求出这个矩阵最小的那一行，具有 $N$ 维， 然后从小到大排序（负的都在前面）

$\arg \text{sort}$ 其实就是返回排序后的下标，在这里就对应了类别，直接返回前 $K$ 小的值，也就对应着 $K$ 个样本的类别

这里有一个假设，也就是一个批次里面没有重复类别的数据，大家需要注意一下！

真实性正则化（Fidelity/Realism Regularization）

这里是借鉴 DeepInversion 中针对图片的自然性的优化

Dreaming to distill: Data-free knowledge transfer via DeepInversion.

文中加入了一个正则化项 ${\mathcal{R}}_{fidelity}(\cdot )$，来驱使生成的 $\hat{x}$ 尽可能保持真实，具体形式为：
$${\mathcal{R}}_{fidelity}(\hat{x})={\alpha }_{tv}{\mathcal{R}}_{TV}(\hat{x})+{\alpha }_{l_2}{\mathcal{R}}_{l_2}(\hat{x})+{\alpha }_{BN}{\mathcal{R}}_{BN}(\hat{x})$$
其中 ${\mathcal{R}}_{TV}$ 和 ${\mathcal{R}}_{l_2}$ 分别惩罚图像的方差和 $L2$ 范数，属于标准的图像先验。

DeepInversion中关键的部分就是使用了BN的先验来进行约束
$${\mathcal{R}}_{BN}(\hat{x})=\sum _l||{\mu }_l(\hat{x})-B{N}_l(mean)|{|}_2+\sum _l||{\sigma }_l^2(\hat{x})-B{N}_l(variance)|{|}_2$$
其中 ${\mu }_l(x)$ 和 ${\sigma }_l^2(x)$ 是第 $l$ 层卷积的，对于一个批数据的均值和方差的估计

这种真实性的正则化能够促使图片变得更加真实

组一致性正则化（Group Consistency Regularization）

在进行训练数据恢复的时候，会有一个挑战，也就是物体实际位置的确定，如下图所示：

在实验中，作者使用了不同的随机种子进行图像的还原，结果产生不同程度上的偏移，但这些样本其实语义上都是一致的。

基于这个观察，作者提出了一种组一致性的正则化方法，也就是用不同的随机种子生成，然后对这些结果进行融合。

其正则化形式为：
$${\mathcal{R}}_{group}(\hat{x},{\hat{x}}_{g\in G})={\alpha }_{group}||\hat{x}-\mathbb{E}({\hat{x}}_{g\in G})|{|}_2$$

其中，我们需要计算出这个期望 $\mathbb{E}({\hat{x}}_{g\in G})$，其实就是平均图像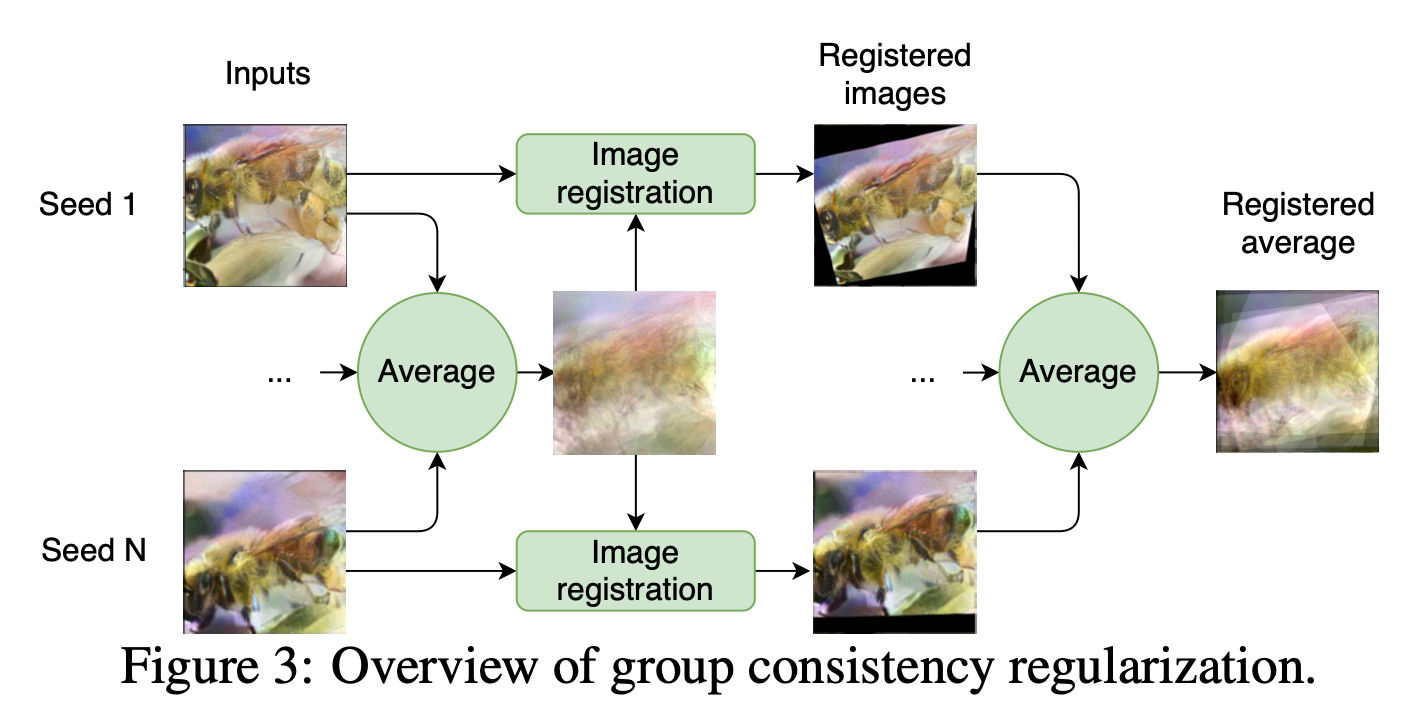

如上图所示，首先按像素进行平均，得到一张平均图像，然后所有图像根据这个平均图像进行对齐，之后再取一次平均，得到最后的对齐后的平均图像。

最终的更新细节

文中使用的是一种基于能量的模型，受 Langevin 的启发，具体形式为
$$\begin{gathered} {\Delta }_{{\hat{x}}^{(t)}}\leftarrow {\nabla }_{\hat{x}}({\mathcal{L}}_{grad}({\hat{x}}^{(t-1)},\nabla W)+{\mathcal{R}}_{aux}({\hat{x}}^{(t-1)})) \\ \eta \leftarrow \mathcal{N}(0,I) \\ {\hat{x}}^{(t)}\leftarrow {\hat{x}}^{(t-1)}+\lambda (t){\Delta }_{{\hat{x}}^{(t)}}+\lambda (t){\alpha }_n\eta \end{gathered}$$
其中 $\eta$ 是采样噪声，用于进行搜索；$\lambda (t)$ 是学习率；${\alpha }_n$ 是缩放因子。

实验分析

首先我们来看一看标签恢复的正确率

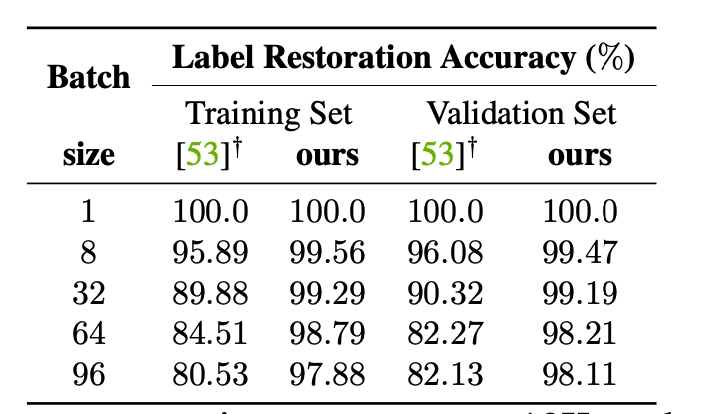
可以看到，随着批次大小的增加，正确率就会下降，原因其实就是重复类别的问题，但是相比起iDLG要好很多。

iDLG: Improved deep leakage from gradients.

然后是每一个误差项的消融实验

可以看到，添加真实性以及组一致性，的确会使得图片质量上升，对齐的增益也是存在的。

如上图所示，基本上还原的结果已经逼近原始图片了

然后，和目前的SOTA进行效果对比，这里直接给出一部分的结果图

可以看到，其效果要比DeepInversion，Latent Projection等工作要好得多！

之后，我们必须看一看批次大小，也就是BatchSize，对于还原效果的影响

可以看到，随着批次大小的增加，还原效果会变差，这也是符合常理的，因为聚合带来的信息损失会增大。

结论

这个工作是里程碑式的，在联邦学习的场景下，实现了一次强而有力的攻击！

这也会极大的启发，针对联邦学习这种类分布式训练的场景下后续的防御工作。

DP等防御方法是否还能适用？参与者的变动是否会有影响？本地的多次训练是否加大了恢复的难度？

仍然有许多工作需要我们一起探索。