CRC8算法的解读，以及在E2E通信保护的应用

已于 2022-10-26 21:34:04 修改
阅读量8.3k 收藏 190
点赞数 18
分类专栏： CANoe和CAPL 文章标签： capl CRC8 循环冗余校验 E2E保护
于 2022-06-30 20:48:41 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_34414530/article/details/125504512
版权

目录

请添加图片描述

📙 CRC8在报文E2E保护中的两种计算方式（预览）

实际仿真工程中仿真报文我们都需要计算Counter和CRC的，以CRC8校验算法为例，下列参数是CRC参数模型

  • // 宽度 WIDTH : 8 bits
  • // 多项式 POLY : x^8 + x^4 + x^3 + x^2 + 1 ==== 0x11d (1-0001-1101)
  • //初始值 INIT : 0x0
  • //结果异或值 XOROUT : 0x0
  • //输入数据反转 : false
  • //输出数据反转 : false
    在这里插入图片描述

🍅 直接计算CRC8校验位

/*@!Encoding:936*/

/****************************************************************************************************  
计算counter 值
***************************************************************************************************/
byte E2E_Counter(byte data[],byte c_pos)
{
  // calculate counter
    int Counter;       
    Counter = data[c_pos] & 0x0F;
    Counter++;
    if(Counter > 15)
      Counter = Counter - 16;
    Counter = (data[c_pos] & 0xF0)+ Counter;
    return  Counter;
}
/****************************************************************************************************  
直接计算CRC8
***************************************************************************************************/


byte E2E_CRC8(byte data[],byte d_length,  byte initial_value)
{
	int i, j;
	int crc8;
	const byte crc_poly = 0x1D;

	crc8 = initial_value; // crc 计算的初始值

	for (i = 0; i < d_length; i++)
	{
    crc8 ^= data[i]; /* 每次先与需要计算的数据异或,计算完指向下一数据 */ 
    
		for (j = 0; j < 8; j++) // 多项式宽度为8，所以需要计算8次
		{
			if (crc8 & 0x80)/* 判断最高位是否为1 */
			{
				crc8 = (crc8 << 1) ^ crc_poly;
			}
			else  /* 最高位为0时，不需要异或，整体数据往左移一位 */
			{
				crc8 <<= 1;
			}
		}
	}
  
	return crc8;
  
}
/****************************************************************************************************  
报文发出回调函数
***************************************************************************************************/

dword applILTxPending (long aId, dword aDlc, byte data[])
{
  dword i;
  byte crc8;
  
  if(aId == 0x322)
  {
    data[6] = E2E_Counter(data,6);   
    data[7] = E2E_CRC8(data,7,0xff);

  }
  
    return 1; // don't prevent sending of the message
}

🍅 查表法计算CRC8校验位

/*@!Encoding:936*/

/****************************************************************************************************  
计算counter 值
***************************************************************************************************/
byte E2E_Counter(byte data[],byte c_pos)
{
  // calculate counter
    int Counter;       
    Counter = data[c_pos] & 0x0F;
    Counter++;
    if(Counter > 15)
      Counter = Counter - 16;
    Counter = (data[c_pos] & 0xF0)+ Counter;
    return  Counter;
}
/****************************************************************************************************  
查表法计算CRC8
***************************************************************************************************/

byte E2E_CRC8_Table(byte data[],byte d_length,byte initial_value)
{
    int i;
    byte crc8;
  
    byte Crc8Table[256] =                                                  
    {
    0x00, 0x1d, 0x3a, 0x27,0x74, 0x69, 0x4e, 0x53,0xe8, 0xf5, 0xd2, 0xcf,   // CRC LOOKUP TABLE
    0x9c, 0x81, 0xa6, 0xbb,0xcd, 0xd0, 0xf7, 0xea,0xb9, 0xa4, 0x83, 0x9e,   // 表生成规则:
    0x25, 0x38, 0x1f, 0x02,0x51, 0x4c, 0x6b, 0x76,0x87, 0x9a, 0xbd, 0xa0,   // ---------------------------------------------------
    0xf3, 0xee, 0xc9, 0xd4,0x6f, 0x72, 0x55, 0x48,0x1b, 0x06, 0x21, 0x3c,   // 宽度 WIDTH : 8 bits
    0x4a, 0x57, 0x70, 0x6d,0x3e, 0x23, 0x04, 0x19,0xa2, 0xbf, 0x98, 0x85,   // 多项式 POLY : x^8 + x^4 + x^3 + x^2 + 1
    0xd6, 0xcb, 0xec, 0xf1,0x13, 0x0e, 0x29, 0x34,0x67, 0x7a, 0x5d, 0x40,   // 0x11d (1-0001-1101)
    0xfb, 0xe6, 0xc1, 0xdc,0x8f, 0x92, 0xb5, 0xa8,0xde, 0xc3, 0xe4, 0xf9,   // [CRC8003]
    0xaa, 0xb7, 0x90, 0x8d,0x36, 0x2b, 0x0c, 0x11,0x42, 0x5f, 0x78, 0x65,   // 初始值 INIT : 0x0
    0x94, 0x89, 0xae, 0xb3,0xe0, 0xfd, 0xda, 0xc7,0x7c, 0x61, 0x46, 0x5b,   // 结果异或值 XOROUT : 0x0
    0x08, 0x15, 0x32, 0x2f,0x59, 0x44, 0x63, 0x7e,0x2d, 0x30, 0x17, 0x0a,   // 输入数据反转 : false
    0xb1, 0xac, 0x8b, 0x96,0xc5, 0xd8, 0xff, 0xe2,0x26, 0x3b, 0x1c, 0x01,   // 输出数据反转 : false
    0x52, 0x4f, 0x68, 0x75,0xce, 0xd3, 0xf4, 0xe9,0xba, 0xa7, 0x80, 0x9d,
    0xeb, 0xf6, 0xd1, 0xcc,0x9f, 0x82, 0xa5, 0xb8,0x03, 0x1e, 0x39, 0x24,
    0x77, 0x6a, 0x4d, 0x50,0xa1, 0xbc, 0x9b, 0x86,0xd5, 0xc8, 0xef, 0xf2,
    0x49, 0x54, 0x73, 0x6e,0x3d, 0x20, 0x07, 0x1a,0x6c, 0x71, 0x56, 0x4b,
    0x18, 0x05, 0x22, 0x3f,0x84, 0x99, 0xbe, 0xa3,0xf0, 0xed, 0xca, 0xd7,
    0x35, 0x28, 0x0f, 0x12,0x41, 0x5c, 0x7b, 0x66,0xdd, 0xc0, 0xe7, 0xfa,
    0xa9, 0xb4, 0x93, 0x8e,0xf8, 0xe5, 0xc2, 0xdf,0x8c, 0x91, 0xb6, 0xab,
    0x10, 0x0d, 0x2a, 0x37,0x64, 0x79, 0x5e, 0x43,0xb2, 0xaf, 0x88, 0x95,
    0xc6, 0xdb, 0xfc, 0xe1,0x5a, 0x47, 0x60, 0x7d,0x2e, 0x33, 0x14, 0x09,
    0x7f, 0x62, 0x45, 0x58,0x0b, 0x16, 0x31, 0x2c,0x97, 0x8a, 0xad, 0xb0,
    0xe3, 0xfe, 0xd9, 0xc4
    }; 
    
    crc8 = initial_value; // crc 计算的初始值
   
    for (i = 0; i < d_length; i++)                     
    {
        crc8 = Crc8Table[crc8 ^ data[i]];
    }  

    return crc8;
}
/****************************************************************************************************  
报文发出回调函数
***************************************************************************************************/

dword applILTxPending (long aId, dword aDlc, byte data[])
{
  dword i;
  byte crc8;
  
  if(aId == 0x322)
  {
    data[6] = E2E_Counter(data,6);   
    data[7] = E2E_CRC8_Table(data,7,0xff);

  }
  
    return 1; // don't prevent sending of the message
}

📙 理解基础：模2 运算

🍅 模2加减法（等同于异或操作）

  • 简单记作： 同0异1
  • 下图1±1 = 0， 写的时候笔误

在这里插入图片描述

在这里插入图片描述

🍅 模2乘法

  • 要点： 中间累加计算时，采用 模2加法 ，也就是结果不进位

在这里插入图片描述

🍅 模2除法

  • 模2除法 不借位减法 ，模2乘法不借位加法 （加法和减法一样，都是异或运算）

  • 除数的首位肯定是1，这是规定，如果是0111，那除数就把0去掉，为111所以除数的首位肯定是1

  • 余数先去掉首位，若此时余数最高位为1，商1，并对以它为除数继续模2除。 若最高位为0，则商0，重复步骤2。

  • 直到余数位数小于除数位数时，运算结束，余数总比除数少一位

  • 如下图： 1111000除以1101： 商为1011 ，余数为111

在这里插入图片描述

在这里插入图片描述

模2除法(CRC)循环冗余校验码在线计算器在线计算平台

📙 理解基础：循环冗余校验

🍅 循环冗余校验简介

所谓循环冗余校验（CRC：Cyclic Redundancy Check）是一种错误检测算法，通常在通信协议中或存储设备中用于检测原始数据的意外变动。可以简单理解成对有用数据按照一定的算法进行计算后，提取出一个特征值，并附加在有用数据后。在应用中将有用数据按照特定的算法提取特征值与预先存储的特征值进行比对，如相等则校验通过，反之校验失败，从而识别出数据是否异常。

🍅 为何要校验数据完整性（Data Integrity）？

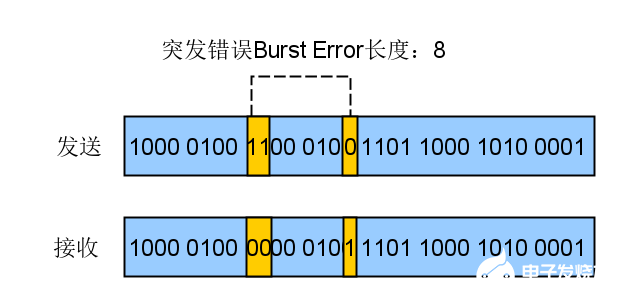
在这里插入图片描述

  • 数据在经过链路层、物理层、通信介质等，传输过程中有可能被干扰到，导致数据传输某些BIT错误
  • 也有可能接收电路、发送电路、调制电路、解调电路都可能由于某些干扰原因导致工作失效而出现误码，所以数据传输要通过校验去确定数据是完整可靠的
  • 循环冗余校验使用二进制除法作为算法原理，具有强大的错误检测机制，在通信领域被广泛使用

🍅 何为循环冗余校验？

  • 这里有n位二进制数据需要被传输 比如 1111 ，根据CRC算法计算出m位冗余码，则实际传输或者存储的就是n+m位二进制数据。
  • m位的冗余码 是多少，那这里引出一个概念：多项式，在CRC校验算法中多项式可做如下理解及表示
  • 比如上面我们做模2除法用的例子，1101，那么他的多项式就是：
  • 根据CRC的规则 冗余码的位数要比 多项式的位数少一位 ，所以 m = 4 -1 =3
  • 根据计算规则，要在要传输的数据后面，补上 m位 0 ，然后根据模2除法计算出 m位冗余码
  • 所以 也就是上面的例子 被除数是 1111000 ，除数是 1101 ，则余数是111
    在这里插入图片描述

📙 CRC的算法原理

🍅 CRC参数模型

前面都是理论基础，那么转换位程序语言该怎么描述和理解呢？

一个完整的CRC参数模型应该包含以下信息：WIDTH，POLY，INIT，REFIN，REFOUT，XOROUT。

  • NAME：参数模型名称。

  • WIDTH：宽度，即生成的CRC数据位宽，如CRC-8，生成的CRC为8位 ，比如我们上面测试用的1111000 模2除以1101 ，则宽度是4，因为后面3个0是模2运算加上去的。

  • POLY：十六进制多项式，省略最高位1，如 x8 + x2 + x + 1，二进制为1 0000 0111，省略最高位1，转换为十六进制为0x07。

  • INIT：CRC初始值，和WIDTH位宽一致。

  • REFIN：true或false，在进行计算之前，原始数据是否翻转，如原始数据：0x34 = 0011 0100，如果REFIN为true，进行翻转之后为0010 1100 = 0x2c

  • REFOUT：true或false，运算完成之后，得到的CRC值是否进行翻转，如计算得到的CRC值：0x97 = 1001 0111，如果REFOUT为true，进行翻转之后为11101001 = 0xE9。

  • XOROUT：计算结果与此参数进行异或运算后得到最终的CRC值，和WIDTH位宽一致。

  • 通常如果只给了一个多项式，其他的没有说明则：INIT=0x00，REFIN=false，REFOUT=false，XOROUT=0x00。

🍅 CRC8查表法，表怎么生成的？

  • 下表列出了CRC8的生成参数，表的大小是256个字节，其实就是0-255（0x00- 0xFF） 这256个数的CRC校验值
    byte Crc8Table[256] =                                                  
    {
    0x00, 0x1d, 0x3a, 0x27,0x74, 0x69, 0x4e, 0x53,0xe8, 0xf5, 0xd2, 0xcf,   // CRC LOOKUP TABLE
    0x9c, 0x81, 0xa6, 0xbb,0xcd, 0xd0, 0xf7, 0xea,0xb9, 0xa4, 0x83, 0x9e,   // 表生成规则:
    0x25, 0x38, 0x1f, 0x02,0x51, 0x4c, 0x6b, 0x76,0x87, 0x9a, 0xbd, 0xa0,   // ---------------------------------------------------
    0xf3, 0xee, 0xc9, 0xd4,0x6f, 0x72, 0x55, 0x48,0x1b, 0x06, 0x21, 0x3c,   // 宽度 WIDTH : 8 bits
    0x4a, 0x57, 0x70, 0x6d,0x3e, 0x23, 0x04, 0x19,0xa2, 0xbf, 0x98, 0x85,   // 多项式 POLY : x^8 + x^4 + x^3 + x^2 + 1
    0xd6, 0xcb, 0xec, 0xf1,0x13, 0x0e, 0x29, 0x34,0x67, 0x7a, 0x5d, 0x40,   // 0x11d (1-0001-1101)
    0xfb, 0xe6, 0xc1, 0xdc,0x8f, 0x92, 0xb5, 0xa8,0xde, 0xc3, 0xe4, 0xf9,   // [CRC8003]
    0xaa, 0xb7, 0x90, 0x8d,0x36, 0x2b, 0x0c, 0x11,0x42, 0x5f, 0x78, 0x65,   // 初始值 INIT : 0x0
    0x94, 0x89, 0xae, 0xb3,0xe0, 0xfd, 0xda, 0xc7,0x7c, 0x61, 0x46, 0x5b,   // 结果异或值 XOROUT : 0x0
    0x08, 0x15, 0x32, 0x2f,0x59, 0x44, 0x63, 0x7e,0x2d, 0x30, 0x17, 0x0a,   // 输入数据反转 : false
    0xb1, 0xac, 0x8b, 0x96,0xc5, 0xd8, 0xff, 0xe2,0x26, 0x3b, 0x1c, 0x01,   // 输出数据反转 : false
    0x52, 0x4f, 0x68, 0x75,0xce, 0xd3, 0xf4, 0xe9,0xba, 0xa7, 0x80, 0x9d,
    0xeb, 0xf6, 0xd1, 0xcc,0x9f, 0x82, 0xa5, 0xb8,0x03, 0x1e, 0x39, 0x24,
    0x77, 0x6a, 0x4d, 0x50,0xa1, 0xbc, 0x9b, 0x86,0xd5, 0xc8, 0xef, 0xf2,
    0x49, 0x54, 0x73, 0x6e,0x3d, 0x20, 0x07, 0x1a,0x6c, 0x71, 0x56, 0x4b,
    0x18, 0x05, 0x22, 0x3f,0x84, 0x99, 0xbe, 0xa3,0xf0, 0xed, 0xca, 0xd7,
    0x35, 0x28, 0x0f, 0x12,0x41, 0x5c, 0x7b, 0x66,0xdd, 0xc0, 0xe7, 0xfa,
    0xa9, 0xb4, 0x93, 0x8e,0xf8, 0xe5, 0xc2, 0xdf,0x8c, 0x91, 0xb6, 0xab,
    0x10, 0x0d, 0x2a, 0x37,0x64, 0x79, 0x5e, 0x43,0xb2, 0xaf, 0x88, 0x95,
    0xc6, 0xdb, 0xfc, 0xe1,0x5a, 0x47, 0x60, 0x7d,0x2e, 0x33, 0x14, 0x09,
    0x7f, 0x62, 0x45, 0x58,0x0b, 0x16, 0x31, 0x2c,0x97, 0x8a, 0xad, 0xb0,
    0xe3, 0xfe, 0xd9, 0xc4
    };

在这里插入图片描述

  • 模2除法 的完整运算测试结果，这里忽略商的值，因为我们要的是余数，看起来很长，只有自己参与运算之后，才能明白
  • 当余数最高位是0的时候，是不需要参与运算的，可以直接借位（补0继续模2运算）
  • 当余数最高位是1的时候，因为除数的最高位永远为1，所以，下个余数的最高位肯定是0，而0又是不需要参与运算，所以可以直接移一位后再进行模2运算

在这里插入图片描述

  • 如果上面的能够理解了，那么简化后的运算如下图，遇到0直接后面补0就好了。
    在这里插入图片描述

在这里插入图片描述

  • 下面是VS 2019下的根据上面的CRC生成参数生成的表源代码
// PrintDeviceInfo.cpp : 定义控制台应用程序的入口点。
#include <stdio.h>
#include <stdlib.h>
#include <locale.h>
#include <Windows.h>

unsigned char crc8(unsigned char value)
{
    unsigned char i, crc;
    crc = value^0x00;
    /* 数据往左移了8位，需要计算8次 */
    for (i = 8; i > 0; --i)
    {
        if (crc & 0x80)  /* 判断最高位是否为1 */
        {
            crc = (crc << 1) ^ 0x1d;
        }
        else
        {
            /* 最高位为0时，不需要异或，整体数据往左移一位 */
            crc = (crc << 1);
        }
    }
    crc = crc ^ 0x00;
    return crc;
}

int  main(int  argc, char* argv[])
{

    unsigned char retCRC;
    unsigned char testValue = 3;
    unsigned char Crc8Table[256];
    
    for(int i =0 ;i< 256 ;i++)
    {
        Crc8Table[i] = crc8(i);

        printf("%5x  ", Crc8Table[i]); 
        if ((i+1) % 12 == 0)
            printf("\n");
    }
	getchar();
	return  0;
}
  • 看下结果，是和上面的表内容一样的：

在这里插入图片描述

  • 理解了模2运算的过程，和下面两句话，那么CRC8的算法核心也就自然明白了
  • 当余数最高位是0的时候，是不需要参与运算的，可以直接借位（补0继续模2运算）
  • 当余数最高位是1的时候，因为除数的最高位永远为1，所以，下个余数的最高位肯定是0，而0又是不需要参与运算，所以可以直接移一位后再进行模2运算
  if (crc & 0x80)  /* 判断最高位是否为1 */
        {
            crc = (crc << 1) ^ 0x1d;
        }
        else
        {
            /* 最高位为0时，不需要异或，整体数据往左移一位 */
            crc = (crc << 1);
        }

🍅 CRC8直接计算法

这个时候再看直接计算的算法，可能就好理解的多，对于在E2E保护中的CRC算法还是建议使用查表法的，因为报文发的很快，CRC校验的速度越快越好。

byte E2E_CRC8(byte data[],byte d_length,  byte initial_value)
{
	int i, j;
	int crc8;
	const byte crc_poly = 0x1D;

	crc8 = initial_value; // crc 计算的初始值

	for (i = 0; i < d_length; i++)
	{
    crc8 ^= data[i]; /* 每次先与需要计算的数据异或,计算完指向下一数据 */ 
    
		for (j = 0; j < 8; j++) // 多项式宽度为8，所以需要计算8次
		{
			if (crc8 & 0x80)/* 判断最高位是否为1 */
			{
				crc8 = (crc8 << 1) ^ crc_poly;
			}
			else  /* 最高位为0时，不需要异或，整体数据往左移一位 */
			{
				crc8 <<= 1;
			}
		}
	}
	return crc8;  
}

在这里插入图片描述

End

🌎总结

23

请添加图片描述

🍅 有需要演示中所用demo工程的，可以关注下方公众号网盘自取啦，感谢阅读。
7

  • 🚩要有最朴素的生活，最遥远的梦想，即使明天天寒地冻，路遥马亡！

  • 🚩 有微信的小伙伴可以关注下浪哥车载诊断，一个行业内小小圈子，群里有网盘资料，源码，还有各路大神 闲时交流交流技术，聊聊工作机会啥的。

  • 🚩如果这篇博客对你有帮助，请 “点赞” “评论”“收藏”一键三连 哦！码字不易，大家的支持就是我坚持下去的动力。
    18
AUTOSAR的E2E通信安全
usstmiracle的博客
07-08 8908
AUTOSAR标准的安全通信为支持功能安全，AUTOSAR标准结合ISO 26262功能安全标准，在基础软件层从安全执行、安全通信以及安全内建测试三个方面做出了规范，并规范 AUTOSAR标准的安全通信 为支持功能安全，AUTOSAR标准结合ISO 26262功能安全标准，在基础软件层从安全执行、安全通信以及安全内建测试三个方面做出了规范，并规范了使用方法，本文主要介绍其安全通信部分。1.安全通信组成部分 为了支持安全通信，AUTOSAR提供了三种机制，数据顺序控制、PDU复制和K/N的投票机制以及端到端
Autosar --- CRC8 SAE J1850 CRC计算
wj博客
01-17 1639
CRC计算一般用于通信中，用来保证一组数据的完整性。发送方发送一组数据dataA+CRC检验码CRCa（CRC校验码由数据算出）；接收方接收到数据dataA+CRC校验码CRCa，接收方通过与发送方约定好的计算公式，计算出一个CRC校验码CRCb， 如果CRCa = CRCb,则表示这一帧数据没有被篡改。有时候为了保证数据的连续性，也会加上一个rolling count。
完整的16位CRC循环校验算法类（c#语言）
anna19850927的博客
04-23 813
/// </summary> /// CRCTAB 表 /// </summary> private static ushort[] crctab = new ushort[256]{ 0x0000, 0x1021, 0x2042, 0x3063, 0x4084, 0x50a5, 0x60c6,...
CRC8算法
热门推荐
简单的过客
11-01 12万+
crc8校验算法、原理、查表法、计算法、c代码
C语言实现查表8位SAE J1850 CRC
最新发布
yeweiliang_93的博客
03-31 571
8位SAE J1850 CRC 查表生成
8.CRC8算法
houshaoyun的博客
06-12 2万+
1、 CRC8标准生成多项式CRC-8 x8+x5+x4+1 0x31（0x131） CRC-8 x8+x2+x1+1 0x07（0x107） CRC-8 x8+x6+x4+x3+x2+x1 0x5E（0x15E）123注：由于多项式的最高为都为1，并且在代码的crc8计算中，最高位也是不使用的， ...
CRC8算法实现
aolizhen5920的博客
09-30 451
通用算法 //CRC-8 x8+x2+x+1 inline unsigned char cal_crc(unsigned char *vptr, unsigned char len) { const unsigned char *data = vptr; unsigned crc = 0; int i, j; for (j = len; j; j--, data++...
CRC-8算法
zgp2917的专栏
01-26 1万+
请移步 CRC8算法_简单的过客-CSDN博客_crc8
易语言CRC32算法汇编源码解读及使用说明
2. CRC算法基础： 循环冗余校验（Cyclic Redundancy Check，简称CRC）是一种根据网络数据包或电脑文件等数据产生较短固定位数校验码的一种散列函数，主要用来检测数据传输或保存后可能出现的错误。CRC广泛应用于数据...
性能测试解读：CRC校验在aec-q100标准下的实际应用与分析
![性能测试解读：CRC校验在aec-q100标准下的实际应用与分析]...文章进一步分析了CRC校验在aec-q100标准下的实际应用，测试流程，以及性能优化的策略。深入分析章节通过对CRC校验错误检测能力的
CRC8算法c语言源代码
08-11
CRC8 的实现算法X2+X+1的源代码。
crc8的校验算法(c语言)
04-29
crc8的校验算法的源代码,用C语言编写的
原创crc8计算方法，直截了当，一看就懂
08-04
计算原理：首先把前面两个数据整合成一个16bit数据，对多项式进行异或运算，求出余数再加上后面的一个字节数据，在进行求余，以此类推，加到最后一个数据结束后，别忘了后面还需要对数据进行补充8个0，于是在左移动8位，对多项式求余数，最后所得为crc值。
【CRC16跨平台编码实践】：在不同平台中实现CRC16算法的兼容性
![CRC16 校验程序 modbus]...在应用实例章节中，深入分析了CRC16在数据通信和软件开发中的实际使用情况。最后，展望了C
CRC8检验算法（C语言实现）
aa25012的博客
09-09 6385
CRC校验算法，简而言之就是把需要校验的数据与多项式进行循环异或(XOR)，XOR的方式与数据传输方式的高位先行(MSB)和低位先行(LSB)有关。那么什么情况算是对齐呢？除数poly的左边的高位的作用其实是给人看的（实际上参与运算的是0011），目的是干掉当前最高位的被除数，本质上是让poly和被除数对齐，然后开始XOR运算。上面的crc计算是纯采用逻辑运行的方式，可以看到，需要的运行量也是不少的，每一个字节。注：由于多项式的最高为都为1，并且在代码的crc8计算中，最高位也是不使用的，
CRC校验算法——以CRC8(X^8+X^2+X+1)为例
weixin_42632414的博客
08-04 8863
前言 RM裁判系统串口通信的帧头用了CRC8校验，借此机会研究了一下CRC校验的原理。 本文以上述帧头作为例子，讲解CRC8(X8+X2+X+1)校验码的生成方法。 帧头定义如图所示： 由图可知： 帧头的数据位总共是4个字节，即32bit； 校验位是1个字节，即8bit。 要从这4字节的数据位生成1字节的CRC校验码。 步骤 设数据位如下： 1.起始字节：0xA5 2.数据长度：0x0002 3.包序号：0x01 连起来就是： A5000201(Hex) = 10100101 00000000 000000
CRC-8算法简记
tangpeng_will的博客
07-14 190
前七个字节左移完了，再与0xFF异或，得到最终校验值。字节0，与多项式异或，左移一个bit，再与多项式异或，再左移一个bit。(也可能是直接再左移)
CRC_8 计算方法及代码实现
08-04 1万+
3). 检测相异或后的CRC寄存器的最高位(第7位)，若最高位为1，CRC寄存器先左移1位，再与多项式0x07H进行异或；(2). 把第一个 8 位数据与 8 位 CRC 寄存器的相异或，把结果放于 CRC 寄存器；(1). 预置 8 位寄存器为十六进制 0x00（即全为 0） ，称此寄存器为 CRC 寄存器；(4). 重复步骤 3 ，直到右移 8 次，这样整个 8 位数据全部进行了处理；(5). 重复步骤 2 到步骤 4，进行下一个 8 位数据的处理；(1). CRC寄存器。......
评论 7
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

蚂蚁小兵

慢慢长夜磨一章好文章，费烟！！

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值