【立体匹配】传统/深度双目立体匹配方法总结

yddcs

已于 2024-08-31 18:04:17 修改

阅读量6k

点赞数 11

分类专栏：双目相机文章标签：相机标定双目深度估计立体匹配投影几何计算机视觉

于 2023-01-30 10:49:16 首次发布

本文链接：https://blog.csdn.net/qq_35200351/article/details/128417101

版权

双目相机专栏收录该内容

5 篇文章

订阅专栏

本文总结了一年的双目立体匹配工作，涵盖相机标定、投影几何、畸变校正和立体匹配的理论与实践。讨论了传统方法如SGBM、AD Census、Patch Match，以及深度学习在立体匹配中的应用，并提供了相关资源链接。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

双目立体匹配工作--2022年度

总述

总述

本篇简单记录自己一年的工作，作为一个总结。博主wx在底部，可拉你进群一起交流成长。

【立体匹配】系列文章matlab标定-1，C++实现校正匹配工作-2，部分参考学习OpenCV–3 ¹

投影几何

针孔模型：

$- x / f = X / Z$ 在此作等价转换，将图像平面移至右边----相机o和物体P间，便于表达

而芯片中心通常不在光轴上，引入两个新的参数 $c_x和c_y$ ，对投影屏幕中心可能存在的偏移进行建模。

how
将世界坐标点 $P （ X ， Y ， Z ）$ 映射到相机平面上坐标点为 $q (x, y)$ 的过程称为 “ 射影变换 ”，可简单表述为：

$\vec q = M· \vec P, \quad\quad where$

where
when

透镜畸变

径向畸变 是由于透镜的形状（筒形）造成的；

切向畸变 是由整个相机的 组装过程 造成的，使透镜与成像平面不平行。
jing
某点的径向位置可用 $r = 0$ 附近的泰勒级数展开式的前几项来描述。
在这里插入图片描述
qie
共需要求出5个畸变系数，按顺序 $k_1,k_2,p_1,p_2,k_3$

在线生成标定板

标定板 https://calib.io/pages/camera-calibration-pattern-generator
在这里插入图片描述

标定

cal
摄像机参数：一般一共15个相关参数：

（1）外参数6个：R 旋转3个参数；T 平移3个参数；

（2）内参数4个： $f_x，f_y，c_x，c_y;$

求解上述10个参数的前提是先假设每次的畸变参数为0；

（3）5个畸变参数： $k_1，k_2，p_1，p_2，k_3；$

其中（2）(3）为摄像机内参数，其中k3普通镜头不使用，鱼眼镜头要使用。

先看 R， T ：

相机拍摄的一个特定物体（世界坐标系），其相对于相机坐标系统的姿态可用旋转和平移进行描述。

三维旋转可拆解为绕每个轴的二维旋转，如依次绕 $x, y, z$ 轴旋转角度 $φ ， θ 和 ξ$ ，则总的旋转矩阵R是 $R_x(φ), R_y(θ),R_z(ξ)$ 三者的乘积。

因此 R 具有其逆矩阵等于其转置矩阵的特性， $R*R^T=R^T·R=I_3$ 。

trans
平移向量是以物体中心为原点的坐标系到以相机中心为原点的坐标系的偏移量，因此，相应的平移向量为 $\vec T=origin_{object}-origin_{camera}$ ,

则，点P在世界坐标系中可表述为 $\vec P_c=R*(\vec P_o-\vec T).$

此时
form
pose

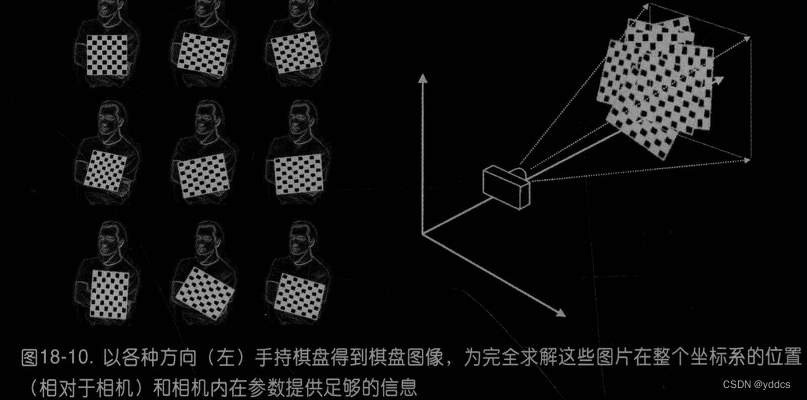
单应性

平面的单应性Homography定义：一个平面到另一个平面的投影映射

齐次坐标表示观察点 $\vec Q$ 和其映射到成像装置的点 $\vec q$ ，则可使用矩阵乘法表示此映射：

在这里插入图片描述

H有两部分：用于定位观察的物体平面的物理变换和使用相机内参矩阵的射影变换，见下图：

在这里插入图片描述
物理变换☞观察物体平面相关的旋转矩阵R 和平移矩阵 T 的影响之和，齐次坐标组合表为：
$\begin{bmatrix}R & \vec t \end{bmatrix}$
我们已经了解如何在投影坐标系中表示相机矩阵M，将其矩阵乘以 $\vec Q$ ，得到：
$\vec q=s*M*W*\vec Q,\quad where \quad M=\begin{bmatrix}f_x & 0 & c_x \\0 & f_y & c_y \\0 & 0 & 1 \end{bmatrix}$ 在这里插入图片描述

单目标定

找棋盘角点

	vector<Point2f> corners1, corners2;
	bool found_1 = cv::findChessboardCorners(src_1, board_size, corners1);
	bool found_2 = cv::findChessboardCorners(src_2, board_size, corners2);

进一步精确至亚像素

	Mat gray_img1;
	cv::cvtColor(src_1, gray_img1, cv::COLOR_BGR2GRAY);
	cv::cornerSubPix(gray_img1, corners1,
		Size(5, 5), Size(-1, -1),
		TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 50, 0.1));
	// 存放当前左视图平面角点
	img_pts1.push_back(corners1);
	cout << "correct! " << img_path.c_str() << endl;

绘制棋盘角点

	/* 在图像上显示角点位置*/
	drawChessboardCorners(src_1, board_size, corners1, true); // 用于在图片中标记角点
	imshow("Camera Calibration", src_1);       // 显示图片
	waitKey(500); //暂停0.5S

draw

/*初始化标定板上角点的三维坐标 假设标定板放在世界坐标系中z=0的平面上*/
void addObjPts(const Size& board_size, const int square_size, vector<Point3f>& obj_pts)
{
	for (int y = 0; y < board_size.height; ++y)
	{
		for (int x = 0; x < board_size.width; ++x)
		{
			obj_pts.push_back(Point3f((double)(x * square_size), (double)(y * square_size), 0.0f));
		}
	}
} // 0 25 50 75 ...
// 存放当前左视图平面角点
img_pts1.push_back(corners1);

re_proj_err1 = cv::calibrateCamera(*obj_pts1,
		*img_pts1,
		img_size,
		K1,
		dist1,
		r_vecs1,
		t_vecs1,
		cv::CALIB_FIX_K3);

双目标定

待双目相机各自标定结束后可使用 cv::stereoCalibrate 进行双目标定

double rms = 0.0;
try {
	rms = cv::stereoCalibrate(obj_pts1,   // input
		img_pts1, img_pts2,				  // input
		K1, dist1,                        // input
		K2, dist2,                        // input
		img_size,                         // input
		R, T, E, F,                       // output
		CALIB_FIX_ASPECT_RATIO + //  固定fx/fy的比值，只将fy作为可变量，进行优化计算。
			// 切向畸变系数（P1，P2）被设置为零并保持为零。
		CALIB_FIX_K3,//CALIB_SAME_FOCAL_LENGTH 强制保持两个相机焦距相同。 | CALIB_USE_INTRINSIC_GUESS  CALIB_FIX_INTRINSIC  
		TermCriteria(TermCriteria::COUNT + TermCriteria::EPS, 100, 1e-5));
} catch (const std::exception&) {
	cout << "Stereo calibration failed, exit the program now.\n";
	return -1; // Stereo calibration failed
}
cout << "rms : \n " << rms << endl;

本征矩阵（Essential Matrix）：包含物理空间中两个相机的旋转平移信息

esse

基本矩阵（Fundamental Mat）：除了包含E中相同的信息外，F还包含两个相机的内参。
在这里插入图片描述

标定后立体校正的理想状态：

$F i g .2.$ 双目相机测距原理图

焦距 $f$ , 基线 $B a se l in e (b)$
$\frac{b}{Z} = \frac{b-(X_R-X_T)}{Z-f}$ 深度Z，视差 $d$
$Z=\frac{fb}{d}, \quad where \quad d=X_R-X_T$

注意事项：

标定板占图像 $1/4 - 1/3$ ，标定板距离远近，各种姿态，全图覆盖，剔除误差大的图像对；
确定相机的视差范围（0， $d$ ）

标定精度评估

在这里插入图片描述

校正

介绍依赖标定的校正方法：Bouguet 算法

给定两幅图像的 $\vec T)$ ，立体校正的Bouguet算法旨在使两幅图像中每幅图像的重投影变化最小化的同时最大化双目视图的公共视野。

在这里插入图片描述
则将左侧相机中极点转换到无穷远处的矩阵即为：

$\quad \quad \quad R_{rect}=\begin{bmatrix}{\vec {e_1}}^T \\{\vec {e_2}}^T \\{\vec {e_3}}^T \end{bmatrix}$

此矩阵将左相机围绕投影中心旋转，使得极线水平且极点位于无穷远处，此时，两个相机可通过如下设置实现行对准：

$\quad \quad \quad R_l=R_{rect}*r_l, \quad \quad and \quad \quad R_r=R_{rect}*r_r.$

Size img_size = src_1.size();
cv::Mat rectifyImageL;// = cv::Mat_<unsigned char>(src_1.rows, src_1.cols);
cv::Mat rectifyImageR;// = cv::Mat_<unsigned char>(src_1.rows, src_1.cols);
/**/Rect validROIL, validROIR;          //图像校正之后，会对图像进行裁剪，这里的validROI就是指裁剪之后的区域  
Mat mapLx, mapLy, mapRx, mapRy;     //映射表  
Mat Rl, Rr, Pl, Pr, Q;              //校正旋转矩阵R，投影矩阵P 重投影矩阵Q
stereoRectify(K11, dist11, K22, dist22, img_size, Ro, Tr, Rl, Rr, Pl, Pr, Q, CALIB_ZERO_DISPARITY,
	0, img_size, &validROIL, &validROIR);
initUndistortRectifyMap(K11, dist11, Rl, Pl, img_size, CV_32FC1, mapLx, mapLy);
initUndistortRectifyMap(K22, dist22, Rr, Pr, img_size, CV_32FC1, mapRx, mapRy);
remap(src_1, rectifyImageL, mapLx, mapLy, INTER_LINEAR);
remap(src_2, rectifyImageR, mapRx, mapRy, INTER_LINEAR);

使用cv::initUndistortRectifyMap()计算矫正映射
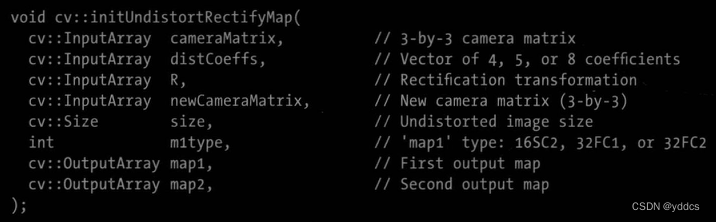
在这里插入图片描述
cv::InputArrat R 此矩阵是补偿相机相对于相机所处的全局坐标系的旋转。

newCameraMatrix 更改相机中心，而不是焦距，处理单目成像时不会使用。

只需矫正一个图像，使用cv::undistort()
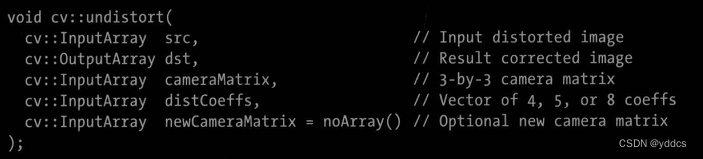
在这里插入图片描述

矫正映射 remap
在这里插入图片描述

校正后结果画线显示：

在这里插入图片描述
细线：原图中画线，粗线为校正图画线

似乎畸变很小欸，但并没有对齐，，

在这里插入图片描述

立体匹配

传统方法

一般分为代价计算，代价聚合，计算视差，后处理等步骤。简单介绍以下三个----SGBM (opencv 内集成有)，AD Census，Patch Match ²

半全局块匹配：

遍历大小为 $n * n$ 的窗口内邻域像素，逐一比较像素值与中心像素值的的大小，计算census值；
与匹配像素逐一计算census值的hamming距离，此汉明距离为匹配代价；或以颜色亮度差值，或梯度值，或组合之，或其他方式作为匹配代价。LBP 算法（Local binary pattern）、SLBP 算法（Support local binary pattern）、FEP算法（Fuzzy encoding pattern）等原理均是计算两个像素的相似性。
4/8邻域内的聚合代价进行相加
视差范围内代价最小的即为匹配视差
左右一致性检查，视差填充，双边中值滤波…

AD-Census：与上述方法略有不同