现在我们去面试,面试官要求我们使用Java写出求解斐波那契数列指定项的函数,可能乍一听很简单,我们在大一的c语言课上就学过递归求解斐波那契数列的指定项,于是大笔一挥,写下如下的第一种解法:
一、递归求解斐波那契数列
public static long fibonacci(int n){
if(n<0)
throw new IllegalArgumentException("Illegal Index");
else if(n == 0)
return 0;
else if(n == 1)
return 1;
else
return fibonacci(n-1)+fibonacci(n-2);
}1、递归本质上是栈,当参数达到一定大小的时候会发生栈移出;
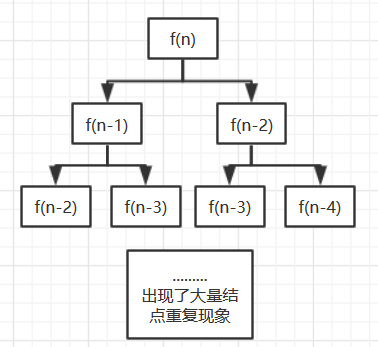
2、从算法实现上来分析,我们要计算fibonacci(n)就需要计算fibonacci(n-1)和fibonacci(n-2),计算fibonacci(n-1)需要计算fibonacci(n-2)和fibonacci(n-3),计算fibonacci(n-2)需要计算fibonacci(n-3)和fibonacci(n-4)......实际上把这个递归算法的递归树画出来,我们会发现很多树结点是重复,也就是我们本来可以不重复计算那么多次;
3、从时间复杂度上来分析,很明显n时的复杂度:f(n)=f(n-1)+f(n-2) 为数学上的二阶常系数差分方程,并且为齐次方程。它的时间复杂度为Ω(ф^n),其中ф为黄金分割数(√5 + 1)/2,Ω表示算法复杂度最小是这么多。也就是说这个算法的复杂度为指数级的复杂度,指数级的时间复杂度我们怎么能容忍?
因此这样的算法只适合帮助我们理解递归,不适合用来真正求解斐波那契数列。
二、从下往上计算,根据f(0)和f(1)计算出f(2),根据f(1)和f(2)计算出f(3),直到计算出第n项
public static long fibonacci(int n){
if(n < 0){
throw new IllegalArgumentException("Illegal Index");
}
else if(n == 0)
return 0;
else if(n == 1)
return 1;
long fibnoacciNMinusOne = 1;
long fibnoacciNMinusTwo = 0;
long fibN = 0;
for(int i = 2; i<=n; i++){
fibN = fibnoacciNMinusOne + fibnoacciNMinusTwo;
fibnoacciNMinusTwo = fibnoacciNMinusOne;
fibnoacciNMinusOne = fibN;
}
return fibN;
}
三、利用数学公式的时间复杂度O(logn)的算法
在代码实现之前,我们需要推导一个公式,首先来看一下斐波那契数列的递推公式:
根据这个公式我们可以得到一个公式:
而且当n=2的时候,以上的公式也是成立的,因此上面的公式在n>=2的时候总成立,所以我们可以得到另一个公式:
我们可以用这个公式来计算斐波那契数列。如果我们从0开始,直到n-1计算矩阵的n-1次幂,时间复杂度仍然是O(n),并不比上面的第二种算法快,我们先实现这种O(n)复杂度的算法:
public static long fibonacci(int n){
if(n<0)
throw new IllegalArgumentException("Illegal Index");
long[][] basicMatrix = {{1,1},{1,0}};
long[][] matrix = calPowerOfMatrix(basicMatrix, n-1);
return matrix[0][0];
}
private static long[][] calPowerOfMatrix(long[][] matrix, int n){//计算matrix与{{1,1},{1,0}}矩阵的n次幂的乘积
for(int i = 0; i<n-1 ; i++){
long a = matrix[0][0];
long b = matrix[0][1];
long c = matrix[1][0];
long d = matrix[1][1];
matrix[0][0] = a + b;
matrix[0][1] = a;
matrix[1][0] = c + d;
matrix[1][1] = c;
}
return matrix;
}但是乘方是具有以下性质的:
利用这个性质,我们可以利用这个公式使用二分法来递归实现斐波那契数列的求解,复杂度可以达到O(logn):
private static long[][] calPowerOfMatrix(long[][] matrix, int n) {
if (n < 0)
throw new IllegalArgumentException("Illegal Index");
else if (n == 1)
return matrix;
else if (n % 2 == 0)// n为偶数
// 如果n为偶数,就计算matrix的n/2次幂的2次幂
return calSquareOfMatrix((calPowerOfMatrix(matrix, n >> 1)));
else// n为奇数
// 如果n为奇数,就计算matrix的n/2次幂的2次幂再乘以matrix
return calBasicMutipyOfMatrix(calSquareOfMatrix(calPowerOfMatrix(matrix, (n - 1) >> 1)));
}
private static long[][] calBasicMutipyOfMatrix(long[][] matrix) {// 计算matrix与{{1,1},{1,0}}的乘积
long a = matrix[0][0];
long b = matrix[0][1];
long c = matrix[1][0];
long d = matrix[1][1];
matrix[0][0] = a + b;
matrix[0][1] = a;
matrix[1][0] = c + d;
matrix[1][1] = c;
return matrix;
}
private static long[][] calSquareOfMatrix(long[][] matrix){//计算matrix的平方
long a = matrix[0][0];
long b = matrix[0][1];
long c = matrix[1][0];
long d = matrix[1][1];
matrix[0][0] = a*a + b*c;
matrix[0][1] = a*b + b*d;
matrix[1][0] = a*c + c*d;
matrix[1][1] = b*c + d*d;
return matrix;
}
public static long fibonacci(int n) {
if (n < 0)
throw new IllegalArgumentException("Illegal Index");
long[][] basicMatrix = { { 1, 1 }, { 1, 0 } };
long[][] matrix = calPowerOfMatrix(basicMatrix, n - 1);
return matrix[0][0];
}








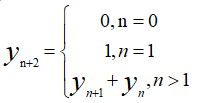


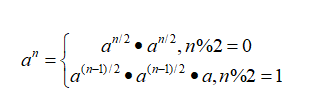














 1860
1860











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








