线性代数知识整理

线性代数知识点整理

 

1.行列式的性质

2.抽象型行列式——解法

3.伴随矩阵的性质

4.逆矩阵的性质

5.逆矩阵——解法

方法一：用伴随

方法二：用初等变换

方法三：用定义

方法四：用单位矩阵恒等变形

方法五：用分块矩阵

6.矩阵的秩定理

定理2

7.矩阵的秩性质

8.具体向量组如何判定相关无关

9.抽象向量组如何证明无关

方法一：用定义

方法二：用秩

方法三：用结论

10.特征值和特征向量的性质

11.相似矩阵的性质

12.矩阵相似对角化的条件

13.正定定理

14.等价、相似、合同

---

1.行列式的性质

2.抽象型行列式——解法

解题思路：对抽象型行列式,计算方法主要是利用行列式的性质，矩阵的性质，特征值及相似等。主要的公式有:

3.伴随矩阵的性质

4.逆矩阵的性质

5.逆矩阵——解法

方法一：用伴随

方法二：用初等变换

方法三：用定义

方法四：用单位矩阵恒等变形

方法五：用分块矩阵

6.矩阵的秩定理

定理2

初等变换不改变A的秩。

行列梯形矩阵的秩等于其非零行数。

注：若零行（若有的话）位于最低行，且每行左起第一个非零元素所在的列下方元素都是0，称这种矩阵为行列式为行阶梯矩阵；

任何矩阵都可通过初等行变换化为行阶梯矩阵。

7.矩阵的秩性质

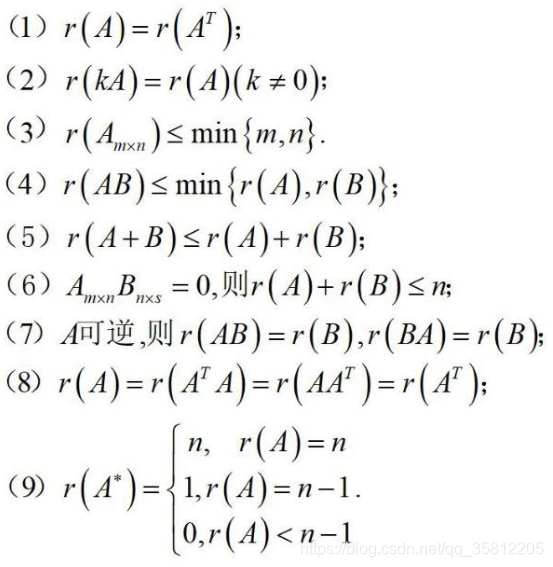
一个结论&证明：

8.具体向量组如何判定相关无关

9.抽象向量组如何证明无关

以三个向量1，2，3为例：

方法一：用定义

方法二：用秩

方法三：用结论

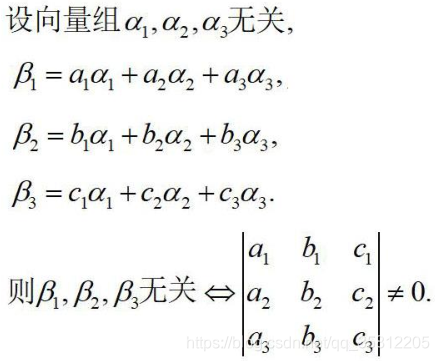
10.特征值和特征向量的性质

11.相似矩阵的性质

12.矩阵相似对角化的条件

13.正定定理

14.等价、相似、合同

下图来自复旦邱锡鹏老师的《神经网络与深度学习》：