【雷达理论基础】

本文编辑：调皮哥的小助理

“雷达”一词是1940 年美国海军创造的英文Radar的音译，源于radio detection and ranging的缩写，意为"无线电探测和测距"，即用无线电的方法发现目标并测定它们的空间位置。

因此，雷达也被称为“无线电定位”，是利用电磁波探测目标的电子设备。雷达发射电磁波对目标进行照射并接收其回波，由此获得目标至电磁波发射点的距离、距离变化率（径向速度）、方位、高度等信息。

雷达的出现，是由于一战期间当时英国和德国交战时，英国急需一种能探测空中金属物体的雷达（技术）能在反空袭战中帮助搜寻德国飞机。二战期间，雷达就已经出现了地对空、空对地（搜索）轰炸、空对空（截击）火控、敌我识别功能的雷达技术。

目前世界上主要存在的传感器有力学传感器、声学传感器、光学传感器、热学传感器、电学传感器以及电磁波传感器，雷达可以认为是电磁波传感器。

本文将解释雷达背后的物理本质帮助读者了解雷达传感器是如何工作的，主要内容有：

1. 电磁波：什么是电磁波？
2. 雷达方程：雷达背后的基本方程
3. 多普勒效应：运动目标的频移
4. IQ 信号：通常采用的信号采样方式
5. 傅立叶变换：基本数据处理技术

1. 电磁波

与其他波一样，电磁 (EM) 波具有反射、折射、衍射以及偏振等效应，可以根据其频率或波长以不同的方式来接收和利用电磁波。波长在千米范围内的电磁波用于超远距离通信，波长在微米范围内的电磁波用于产生可见光谱，而波长在皮米范围内的电磁波用于医学研究，被称为 X 射线。

$f=\frac{c}{\lambda }=\frac{\text{ speed of light }}{\text{ wavelength }}$

对于毫米波雷达，其波长在毫米范围内，24GHz雷达系统的波长 λ 为：

$\lambda =\frac{c}{f}=\frac{3\cdot 10^8\mathrm{m}/\mathrm{s}}{24\mathrm{GHz}}=12.5\mathrm{mm}$

雷达系统中的天线在射频前端将电压和电流转换为电磁波，并在接收端将电磁波转换为电压和电流。

2. 雷达方程

在雷达系统中，电磁波从发射(TX)天线发射，然后在空间中传播，直到击中目标后被反射并返回接收(RX)天线。

为了检测这种反射信号，它必须高于雷达系统的最小可检测信号。该最小信号通常与噪声水平进行比较，该比率称为最小信噪比 ( $SN{R}_{\min }$ ) 。

接收信号的功率对雷达的性能非常关键，因为它定义了可探测目标和不可探测目标之间的差异，该值由著名的雷达方程表示：

$P_{rx}=\frac{P_{tx}{G}_{tx}{G}_{rx}\sigma {\lambda }^2}{(4\pi {)}^2{R}^4}$

关于发射功率与目标检测距离的关系可以通过下面的网页小程序演示。网址：https://www.infineon.com/cms/en/product/promopages/makeradar/makeradar-school/radar-theory/

雷达方程表明了接收功率受多个变量的控制。正如预期的那样，功率随距离R迅速下降，该距离由 $(1/R{)}^4$ 控制，其中 R 是雷达和目标之间的距离。

功率也由收发天线的增益 $G_{tx}$ 和 $G_{rx}$ 决定，该增益是天线效率的量度，以及天线将能量集中在目标方向上的程度。

显然，接收功率也会增加发射功率水平 $P_{tx}$ ，此外，不同的目标还会以不同的方式反射电磁波。例如，一个大的金属物体会比一个小的网球反射更多的能量，这在具有雷达横截面 σ 的雷达方程中可以找到相关的说明。

${\lambda }^2$ 显示了接收功率对波长和频率的依赖性，即发射信号的频率越高，接收到的功率越低。例如在其他条件相同的情况下，24G雷达接收功率会比77G雷达的接收功率高。

3. 多普勒效应

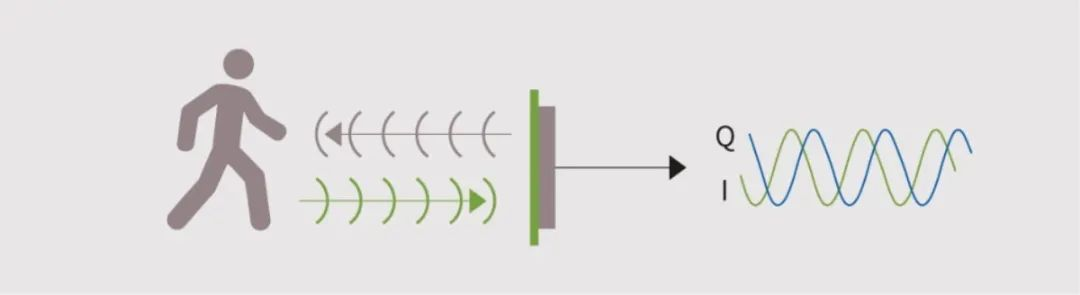
在生活中我们每个人都体验过多普勒效应，最常见的是当救护车从你身边经过时声音大小的突然变化，当救护车靠近你时声音会越来越大，救护车远离你时，声音会越来越小，这就是多普勒效应。

如果波源朝着观察者的方向行进，波峰间的距离越来越近（频率向上移动）时，如果波源正在远离观察者，则波峰间的距离越来越远（频率向下移动）。

电磁波的频移 f 可以直接从原始波频率 f0和波源相对于观察者的速度v推导出来，表示如下：

$f=\left(1+\frac{v}{c}\right)f_o$

多普勒雷达的工作原理是通过发射天线发送一个频率，该频率被目标反射回来，由接收天线捕获。如果目标正在移动，则此接收到的信号频率将根据目标的速度移动。多普勒雷达的接收器使用一个特定的模块（混频器），它根据发射和接收的信号产生输出信号。该模块的输出具有一个频率，该频率等于发射信号和反射信号之间频率的绝对差，也称为多普勒频移。

4. IQ正交信号

IQ 信号具有相同幅度和频率，但相对于彼此偏移 90° 或四分之一周期的信号，换句话说，即两个信号彼此正交。

雷达系统要么有实信号的接收链路，要么有复信号的接收链路。实信号的接收链路只有一个接收信号分量，复信号的接收链路将同时生成 I 和 Q 分量。

IQ 信号有几个优点：
（1）IQ信号便于调制。
例如，一个正弦信号，有三个变量，振幅、频率和相位，所谓调制就是对正弦信号的振幅、频率或相位进行调制，而有了IQ信号，只需要改变IQ信号的幅度，就可以实现这些调制。

（2）可以减少对滤波器抑制度的要求
例如，从时域上来分析，设输入信号为 $\sin \left(2\pi f_{1}t\right)$ ，本振信号为 $\sin \left(2\pi f_{2}t\right)$ ，则输出信号为 :

$\sin \left(2\pi f_{1}t\right)\ast \cos \left(2\pi f_{2}t\right)+\cos \left(2\pi f_{1}t\right)\ast \sin \left(2\pi f_{2}t\right)=\sin \left(2\pi \left(f_1+f_2\right)t\right)$

因此只有一个边带的信号，另外一个边带相消了（数学上的运算）。即使链路中存在不理想性，另外一个边带中的能量也要比常规单混频器架构的低，这降低了对发射滤波器抑制度的要求，这也是正交调制器相对常规混频方案的优势所在。

关于这部分内容，后面会单独写一篇文章详细推导IQ调制的推导过程。

（3）数字正交（IQ）采样对ADC的要求比较低。
可以处理较宽的基带信号，对A/D变换器的转换速率要求也相对较低。

但是，在多普勒雷达里，由于多普勒雷达接收机中使用的实混频器，没有目标运动方向的绝对频移，因此无法确定目标的行进方向。如果使用IQ混频器，它同时产生I和Q信号，通过检查哪个信号在相位上超前，就可以确定运动的方向。

5.傅里叶变换

5.1 离散傅里叶变换（DFT）

电信号可以通过多种方式可视化：如果您将来自英飞凌芯片的 24 GHz 信号连接到高速示波器，您将看到一个正弦波，它是一个时域信号。如果您决定将信号连接到频谱分析仪，您将看到一条 24 GHz 的线条。

DFT 将有限离散信号从时域变换到频域的一种数学变换，反之，逆傅立叶变换将有限离散信号从频域转换到时域。

对于长度为T且采样时间为 $\Delta t$ 的离散时域信号，DFT表示的离散信号将具有最大频率 $F=\frac{1}{2\Delta t}$（奈奎斯特频率）和频率分辨率 $\Delta f=\frac{1}{T}$（也称为 bin 间距） 。，且DFT 生成的一系列复数表示了信号频率的幅度和相位信息。

5.2 快速傅里叶变换（FFT）

FFT是一种将时域采样信号转换为频率分量的算法，DFT的计算复杂度为O(n2)，而FFT算法的计算复杂度为O(n⋅log(n))，其中n为级数的长度。

如果将FFT应用于实信号数据(非IQ)，则会生成具有正频率和负频率的对称频谱，但我们只对正频谱区域的雷达信号分析感兴趣。

另一方面，如果使用复数的输入数据(IQ），FFT将产生一个正的频谱，离散信号的最大频率为$F=\frac{1}{\Delta t}$ ，是实信号FFT的两倍，不过这也是符合奈奎斯特频率定理的，因为对IQ信号的FFT相当于只在采样率加倍的情况下对实信号进行采样。

这句话怎么理解呢？

假设，我们同时对某个固定时间长度的信号进行采样，实采样点数为128个点，得到的数据是实数，复采样也是128个点，但是得到的数据是复数。按照两个实数组成一个复数的定义，其实复采样采集了256个点，只是IQ两路个128个，然后组成了128个复数点，因此说：IQ信号的FFT相当于只在采样率加倍的情况下对实信号进行采样。

参考资料

[1]https://www.infineon.com/cms/en/product/promopages/makeradar/makeradar-school/radar-theory/