STAT313 Chap3 Histogram 讲义解析（二）

本文原创笔记，禁止转载。有问题可私信付费找我咨询。

通过最小化均方误差（MSE）来选择合适的箱宽

这部分讲解了如何通过最小化均方误差（MSE）来选择合适的箱宽 $h$ ，从而达到偏差与方差的权衡。

均方误差是衡量估计器准确性的常用指标，它包含了偏差（bias）和方差（variance）两个部分：

$$\text{MSE}(\hat{\theta })=E[(\hat{\theta }-\theta {)}^2]=\text{bias}(\hat{\theta }{)}^2+\text{Var}(\hat{\theta })$$

以上公式是可以推导出来的。

$\text{bias}(\hat{x})=\left|E[{\hat{f}}_n(x)]-f_X(x)\right|=hL$

$\text{Var}(\hat{x})=Var({\hat{f}}_n(x))=\frac{f_X(x)}{nh}+\frac{L}{n}$

对于直方图密度估计器 ${\hat{f}}_n(x)$ ，MSE可以被分解为偏差的平方和方差。根据幻灯片上的不等式，MSE 的上限是：

在这个不等式中， $h^2{L}^2$ 对应偏差的平方， $\frac{f_X(x)}{nh}$ 和 $\frac{L}{n}$ 对应方差。为了最小化MSE，我们需要在偏差和方差之间找到一个平衡点。幻灯片提出，如果我们选择 $h_n={\left(\frac{f_X(x)}{2L^{2}n}\right)}^{\frac{1}{3}}$ ，则能在理论上最小化MSE的上界。但是，由于 $f_X(x)$ 和 $L$ 是未知的，我们不能直接计算出这个最优的 $h_n$ ，因为它依赖于未知的真实概率密度函数 $f_X(x)$ 和利普希茨常数 $L$ 。

在实际应用中，我们通常无法直接计算最优箱宽，但是可以使用一些启发式方法，如交叉验证，来近似这个最优值。例如，我们可以对不同的箱宽 $h$ 进行实验，计算每个 $h$ 对应直方图估计的MSE，并选择那个使MSE最小的箱宽。这通常涉及到使用核密度估计（KDE）作为MSE的近似来实现。

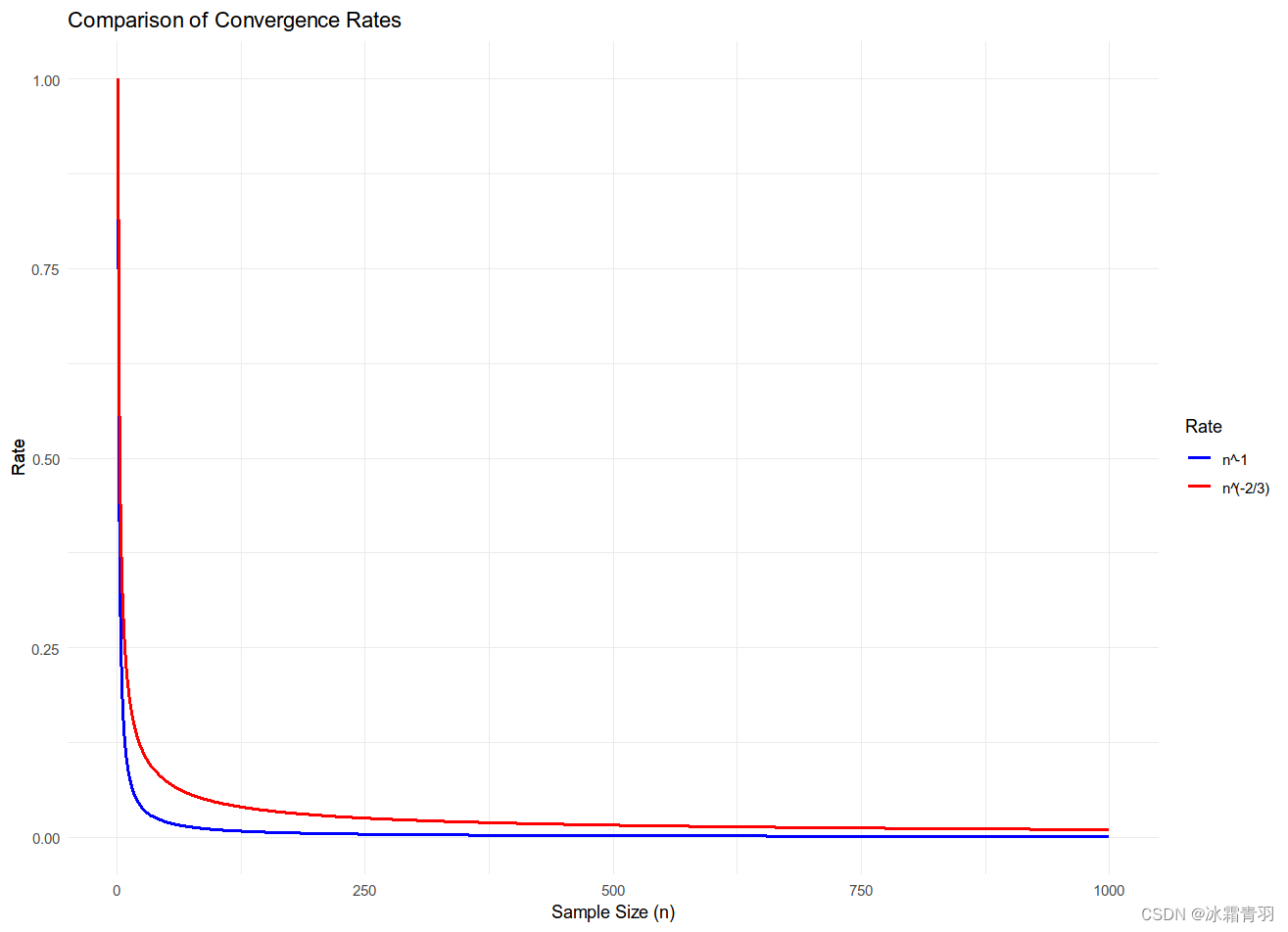
即使我们不能选择最优的 $h_n$ ，选择 $h_n=c{n}^{-\frac{1}{3}}$ 也可以使MSE达到 $C{n}^{-\frac{2}{3}}$ ，其中 $c$ 和 $C$ 是常数，通常不需要具体计算。这表示MSE随样本量 $n$ 增加而减少的速率为 $n^{-\frac{2}{3}}$ 。这是在大样本极限下的收敛速率，它告诉我们估计器的准确性如何随着样本大小的增加而提高。

幻灯片表明，即使我们无法选定最优的箱宽 $h_n$ ，也可以选择一个箱宽，使得MSE的收敛速率接近最优。如果我们选择 $h_n=c{n}^{-\frac{1}{3}}$ ，其中 $c$ 是一个常数，那么MSE的上界可以被控制在 $C{n}^{-\frac{2}{3}}$ 的量级上，其中 $C$ 也是一个常数。这意味着MSE与 $n^{-\frac{2}{3}}$ 成正比，是样本大小 $n$ 的一个函数。

通常我们关心的是随着样本大小 $n$ 增加，MSE下降的速率（而不是具体的常数）。因此，我们可以说直方图估计器的MSE是 $O(n^{-\frac{2}{3}})$ ，这里的大O符号表示上界是 $n^{-\frac{2}{3}}$ 的量级。

当我们说 $O(n^{-1})$ 是比 $O(n^{-\frac{2}{3}})$ 更快的收敛速率时，原因在于 $n^{-1}$ 随着 $n$ 的增加下降得更快。这可以通过比较两者的幂次来直观理解：

$n^{-1}$ 表示随着样本量增加，误差按照 $n$ 的倒数减少。

$n^{-\frac{2}{3}}$ 则表示误差减少的速度慢于 $n$ 的倒数。

由于 $-1$ 比 $-\frac{2}{3}$ 更小，所以 $n^{-1}$ 的衰减更快。在实际应用中，这意味着如果两个估计方法的误差分别以这两种速率减少，那么采用 $n^{-1}$ 的方法将能更快地得到更精确的结果。

具体到这个直方图和经验分布函数的例子中，经验分布函数（EDF）的均方误差（MSE）收敛速率为 $O(n^{-1})$ ，这说明其统计效率高于直方图估计的 $O(n^{-\frac{2}{3}})$ ，从而在相同的样本量下，经验分布函数的估计结果通常会更接近真实分布。

Landau symbols

这张幻灯片介绍了Landau符号，这是在数学中描述函数或数列增长行为的一种符号系统。

$x_n=o(a_n)$ 表示当 $n\to \infty$ 时， $\frac{x_n}{a_n}$ 的极限是 0。也就是说， $x_n$ 相对于 $a_n$ 增长得非常慢，以至于其比值趋于零。

$x_n=O(a_n)$ 表示当 $n\to \infty$ 时， $\frac{|x_n|}{|a_n|}$ 是有界的。也就是说， $x_n$ 的增长速率不会超过 $a_n$ 的某个常数倍。

小o 和 大O 的直观例子（包含图示）

小o表示 $x_n$ 的增长速度比 $a_n$ 慢，而大O表示 $x_n$ 的增长速度不会比 $a_n$ 快。

在直方图估计器的MSE的背景下，使用这些符号可以帮助我们了解随着样本量 $n$ 的增长，MSE减小的速率。例如，如果我们有 $\text{MSE}({\hat{f}}_n(x))=O(n^{-\frac{2}{3}})$ ，这说明MSE随样本量 $n$ 的增长以 $n^{-\frac{2}{3}}$ 的速率减小。这种表达忽略了常数因子，只关注最主要的变化趋势。

第二张幻灯片显示的是经验分布函数（Empirical Distribution Function, EDF），用于估计实际数据的分布。这里给出的例子是205名加拿大工人的对数收入的经验分布。图中的 $F_n(x)$ 表示经验分布函数， $x$ 轴代表对数收入的数值。图中提到，密度在12和14附近有模态（modes），也就是说在这些值附近数据点较多，而且这些点的经验分布函数的斜率较大，表明数据在这些区间集中。

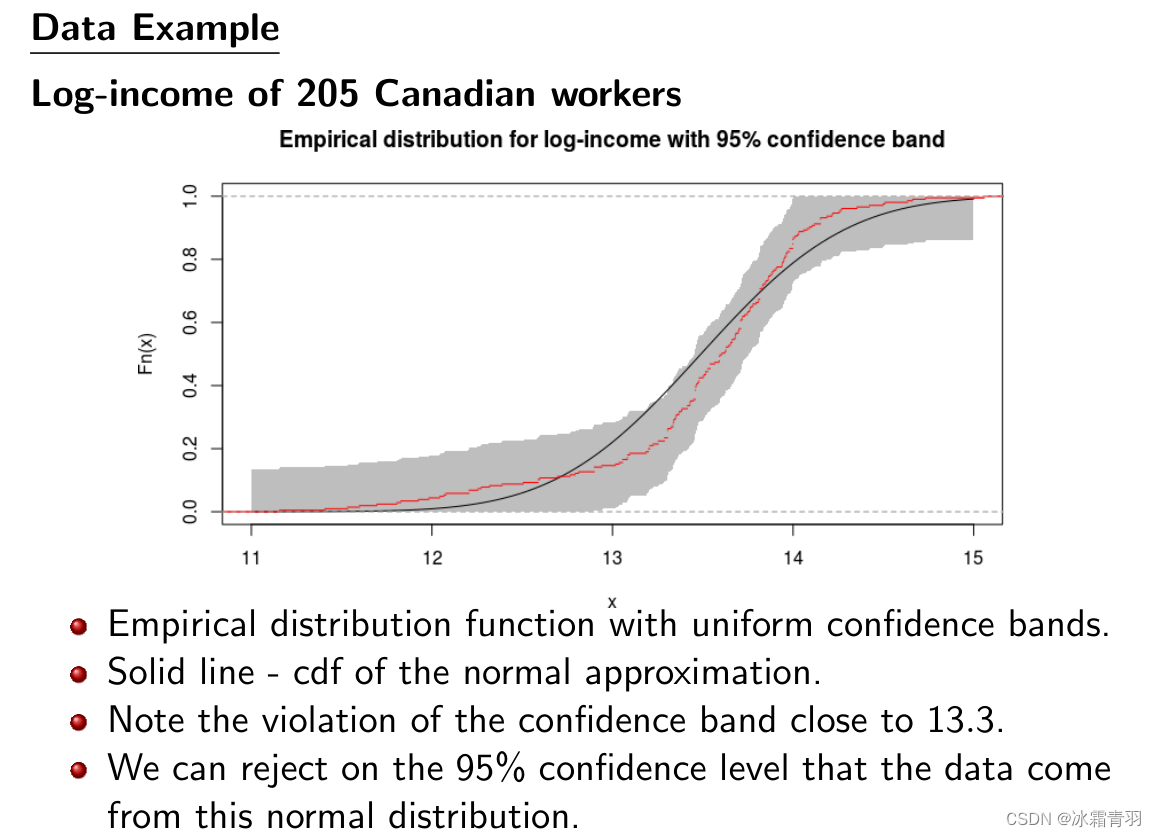
这张幻灯片展示了具有95%置信区间的经验分布函数（EDF）以及对数收入数据的正态分布近似的累积分布函数（CDF）。置信带是用来评估观察到的经验分布与特定理论分布（这里是正态分布）之间的一致性。

从图中可以看出：

红色实线表示205名加拿大工人对数收入的经验分布函数（EDF）。

灰色区域表示95%置信带。这意味着我们预期，在该理论分布是正确的情况下，经验分布函数的真实线将在灰色区域内95%的时间。

注意图中指出在x约为13.3的位置，经验分布函数突破了95%置信带。这通常意味着在这个点，实际观察到的数据与正态分布的预期有显著差异。

基于这种观察，幻灯片下方的文字提出了一个结论，即我们可以在95%的置信水平上拒绝数据来自这个正态分布的假设。换句话说，**有足够的证据表明，这些对数收入数据不遵循正态分布。**这种测试是统计学中的假设检验的一个例子，在这种情况下，似乎违反了正态性的假设。这可能提示我们使用其他分布模型来更好地描述数据，或者探索数据中的异常值和偏态。

直方图的箱宽太宽，这使得我们失去了很多有关数据分布细节的信息。较大的箱宽可能会隐藏一些数据的变化模式，如峰值和谷值。

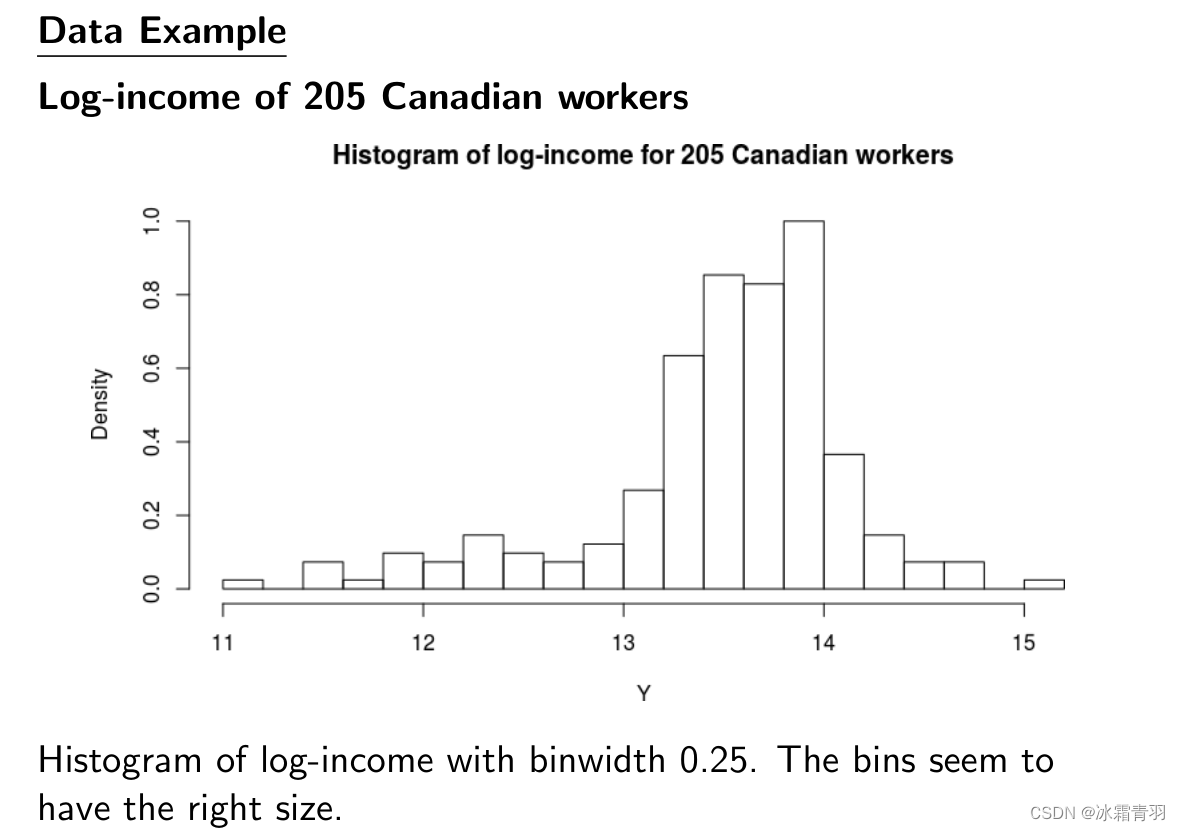
这里的箱宽看起来合适，因为它揭示了数据的分布特点，同时避免了过于细碎的细节。合适的箱宽能平衡细节和总体趋势的可视化。

直方图的箱宽太小，导致直方图中出现了许多箱，这可能会引起过度解读数据中的随机波动作为实际的变化模式。

在统计学中，选择合适的箱宽是重要的，因为它影响我们对数据结构和分布的理解。过大或过小的箱宽都会导致误解。通常，选择箱宽是基于数据的性质和分析者希望传达的信息，有时也会用某些规则或公式来确定最佳的箱宽。例如，Scott’s rule和Freedman-Diaconis rule就是用来估算理想箱宽的常用方法。在实际应用中，可能还需要结合数据的特征和分析目的来手动调整箱宽，以便更好地揭示数据的分布情况。

le和Freedman-Diaconis rule就是用来估算理想箱宽的常用方法。在实际应用中，可能还需要结合数据的特征和分析目的来手动调整箱宽，以便更好地揭示数据的分布情况。