第二章 多臂老虎机（一）

第二章 多臂老虎机

1. 两种反馈：纯估计性反馈（purely evaluative feedback）和纯指示性反馈（purely instructive feedback）
   纯估计性反馈：估计某个动作好坏的程度，而不是该动作是否最好或者最坏。依赖于实际采取的动作。
   纯指示性反馈：指示正确的动作，与实际采取的动作无关。这种反馈是监督学习的基础。
2. 本章学习目标：研究这两种反馈的区别与联系。

2.1 k臂老虎机问题（k-armed Bandit Problem）

1. 问题描述：在k个操作（options）或者动作（actions）中选择一个，并且重复选择。每一次选择之后将会收到一个数值的奖励，这个奖励采样于一个静概率分布，这个概率分布是基于所选择动作的。
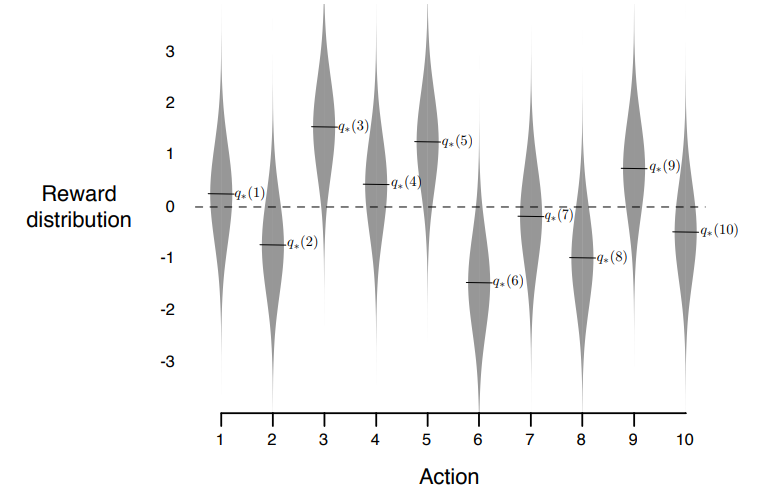
   如下面图示，以高斯分布为例，二维情况下，a为动作a对应奖励的概率分布，*是我们的采样，是我们最后得到的实际奖励R。b、c是其他动作对应的奖励概率分布。类似的，我们可以在一维情况下采样。
   

2. 目标：在一些时间步（time steps）后，比如1000步之后，最大化期望总奖励（expected total reward）。
3. 在k臂老虎机问题中，每一次选择动作都有动作对应的期望（expected）或者平均（meaning）的奖励，称为动作值（the value of that action），时刻t选择的动作记为$A_t$，相关的奖励记为$R_t$。任给动作a，对应的期望奖励记为$q_{\ast }(a)$，$q_{\ast }(a)\doteq \mathbb{E}[R_t|A_t=a]$。若已知所有的动作值函数，k臂老虎机就很好解决了——我们只需要选择值最高的动作。但我们假设的情况是，动作值不可知，但可估计。称时刻t动作a对应的估计值为$Q_t(a)$，我们希望$Q_t(a)$接近实际值$q_{\ast }(a)$。
4. 选择动作值$Q_t(a)$最大的动作$a$称为贪婪动作，当我们采取贪婪动作的时候，称我们在钻研/开发（exploiting） 动作值；当不采取贪婪动作时，称我们在调查/探索（exploring）。探索可以提升非贪婪动作的值。在单步中，开发可以最大化期望奖励；在多步中，探索有利于得到更高的总奖励。
5. 在本章中，我们提出几个简单平衡探索-开发问题的方法，并且证明它们比纯开发的效果更好。

2.2 动作值方法

1. 动作值方法：➀、估计动作值；➁、根据估计值选择动作。
2. 抽样平均方法（sample-average） 用于估计动作值：
   $q_{\ast }(a)$是我们的目标，即选择的动作的平均值。我们构造：
   $Q_t(a)\doteq \frac{sumofrewardswhenatakenpriortot}{numberoftimesatakenpriortot}=\frac{{\sum }_{i=1}^{t-1}{R}_i\cdot 1_{A_i=a}}{{\sum }_{i=1}^{t-1}{1}_{A_i=a}}$
   其中，$1_{predicate}$是指示函数，若断言$predicate$正确，值为1，否则为0。若分母为0，默认$Q_t(a)=0$。根据大数法则，当分母趋于无穷时，即无限多次选择之后，$Q_t(a)$将会收敛到$q_{\ast }(a)$。当然，抽样平均方法并不是估计动作值最好的方法，但我们在这里不做展开。
3. 纯贪心的动作选择方法（greedy action selection method）（根据估计值选择动作（一））：取估计值最大的动作，如下：
   $A_t\doteq \arg \underset{a}{\max }{Q}_t(a)$，贪心动作选择方法只会钻研最好的动作值，使它们最大化，并不会调查那些看起来没那么好的动作值，但事实上，可能较次的实际拥有更高的动作值。
4. $ϵ$-贪心方法（$ϵ$-greedy method）（根据估计值选择动作（二））：大多数时候遵照贪心法则，只有$ϵ$的概率会随机选择一个动作。好处是当步数增多时，每一个动作都将被采样无限多次，所以保证了所有的$Q_t(a)$都收敛到$q_{\ast }(a)$。
5. 练习：在$ϵ$-贪心动作选择法中，假如有两个动作，以及$ϵ=0.5$，那么贪心动作被选择的概率是多少？
   解：假设有动作a、b，且$Q(a)>Q(b)$，那么a是贪心动作。
   $$\begin{gathered} P(\pi =a)=P(\pi =a，\pi isgreedy)+P(\pi =a，\pi isnotgreedy) \\ =1\ast (1-0.5)+\frac{1}{2}\ast 0.5 \\ =0.75 \end{gathered}$$
   由公式可知，此时贪心动作被选择的概率是0.75。

2.3 10臂测试平台（10-armed testbed）

6. 工作机制：每一次运行， 都依高斯分布（均值为0，方差为1的正态分布）随机选出10个值作为$q_{\ast }(a)$（每个动作a对应的真实值）。在时间步t选择的动作$A_t$，对应的反馈是$R_t$，其中$R_t$采样于均值为$q_{\ast }(a)$，方差为1的正态分布。并且运行多次，例如2000次，注意每次都重新随机生成$q_{\ast }(a)$。
   
   

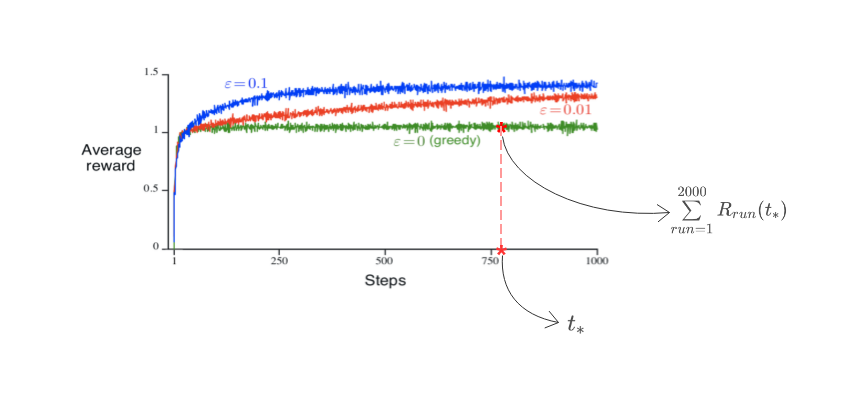
7. $ϵ$-贪心算法与纯贪心算法的区别：下图是运行2000次得到的性状图，其中动作值估计和最有动作比都是使用了抽样平均方法。可以看出，纯贪心算法最初会提高很快，但逐渐收敛到较低的平均奖励上，约为1；而$ϵ$-贪心算法可收敛到1.55。所以，纯贪心算法在长时间运行的条件下相对劣势，经常收敛到局部最优动作上。

8. $ϵ$-贪心算法的优势取决于任务的设定，若方差高，则效果好；反之，则效果不佳。另外，如果我们弱化假设，那么$ϵ$-贪心算法将变得很重要。例如，我们假设k臂老虎机不稳定。不稳定性是强化学习最常见的问题。即使我们假设环境是稳定且确定的，我们的小实验中的$R_t$仍然每一次都不一样。因此探索/调查的模式必不可少。实际强化学习中我们需要平衡探索和开发。
9. 练习：
   2.2. 假设4-臂老虎机中，动作为1、2、3、4，使用$ϵ$-算法，和样本平均方法估计。初始值$Q_1(a)=0,foralla$，初始动作及值分别是$A_1=1,R_1=-1,A_2=2,R_2=1,A_3=2,R_3=-2,A_4=2,R_4=2,A_5=3,R_5=0$。在其中一些步，$ϵ$可能会发生，那么哪些步下，一定发生？哪些步下可能发生？
   解：

run \ action	1	2	3	4	(selected action)	(reward)	$ϵ$
1	0	0	0	0	1	-1	possible
2	-1	0	0	0	2	1	possible
3	-1	1	0	0	2	-2	definitely no(若默认$ϵ$不选择最优动作，否则设为possible )
4	-1	-0.5	0	0	2	2	definitely yes
5	-1	0.33	0	0	3	0	definitely yes
6	-1	0.33	0	0

根据上面的表表格可知，$ϵ$在第4、5步一定发生，在第1、2、3步可能发生。
2.3. 在上面的性状图中，就积累奖励与选择最佳动作比而言，哪一个方法在长期运行中性状更优？优多少？请有质量的作答。
解：就积累奖励而言，$ϵ$-方法更优。在长期运行之后，$ϵ$可以得到非$ϵ$的1.5倍的奖励。就选择最佳动作比而言，在长期运行之后，$ϵ$方法能够达到91%，而非$ϵ$只有不到40%，$ϵ$大约是非$ϵ$的2.3倍。

2.4 递增实现（incremental implementation）

1. 上一节介绍了使用样本平均的方法估计奖励，这一节将介绍如何更有效率地估计奖励的平均值，该方法有固定的记忆空间和固定的每步计算量。首先给一些定义：
   称$R_i$为执行第i个动作得到的奖励。
   称$Q_n$为该动作执行完n-1次后的平均值，即$Q_n\doteq \frac{R_1+\cdots +R_{n-1}}{n-1}$。
   我们每次算样本平均时，总会执行以上操作，随着步数的增加，我们需要存储的 记忆空间 { R 1 , R 2 , . . . , R n − 1 } \{R_{1},R_{2},...,R_{n-1}\} {R1​,R2​,...,Rn−1​}会随之变大，而且计算量也会随之增大。事实上，这不是必要的，我们可以做等价替换，使其表达为递增的形式，称为递增实现。
2. 只需给出$Q_n$与$R_n$，新的n个奖励的平均值可计算如下：
   $$\begin{array}{rl}{Q}_{n+1}& =\frac{1}{n}\sum _{i=1}^n{R}_i\\ & =\frac{1}{n}\left(R_n+\sum _{i=1}^{n-1}{R}_i\right)\\ & =\frac{1}{n}\left(R_n+(n-1)\frac{1}{n-1}\sum _{i=1}^{n-1}{R}_i\right)\\ & =\frac{1}{n}\left(R_n+(n-1)Q_n\right)\\ & =\frac{1}{n}\left(R_n+n{Q}_n-Q_n\right)\\ & =Q_n+\frac{1}{n}\left[R_n-Q_n\right]\end{array}\text{\hspace{1em}(1)}$$
   特别的，当$n=1$时，对于任意的$Q_1$，$Q_2=R_1$。对于（1）式，我们需要的只是两个变量的储存空间，和每一步十分简单的计算量。
   公式（1）将在书中频繁出现，一般形式为：
   $NewEstimate\leftarrow OldEstimate+StepSize[Target-OldEstimate]$
   其中，$[Target-OldEstimate]$称为估计的误差，其中$Target$可以看作是理想方向，这里的$Target$对应着第n个奖励。$StepSize$称为步长因子，本书中我们常用$\alpha$表示，或者${\alpha }_t(a)$。
3. 伪代码：样本平均方法+$ϵ$-贪心算法
   

2.5 一个不稳定问题

1. 由上一节可知，平均法适用于稳定性老虎机问题，即奖励的概率不随时间改变。但是现实中大多数强化学习具有强不稳定性。在这种情况下，我们的解决方案是权重上更偏向于最近的奖励，并且减少很早之前奖励的权重。
2. 解决方案一：常数步长因子。
   以公式（1）代表的递增实现为实例，即以$Q_n$和$R_n$更新$Q_{n+1}$。
   下面的工作是：讨论在步长因子$\alpha$为常数的情况下，$Q_n$与前n-1个奖励 { R i } i ∈ [ 1 , n − 1 ] ∩ Z \{R_{i}\}_{i\in [1,n-1]\cap\mathbb{Z}} {Ri​}i∈[1,n−1]∩Z​的关系。
   $Q_{n+1}\doteq Q_n+\alpha \left[R_n-Q_n\right]$，其中$\alpha \in (0,1]$是常数。可以一次推出，$Q_n$是前n-1个奖励和初始估计值$Q_1$的加权平均：

$$\begin{array}{rl}{Q}_{n+1}& =Q_n+\alpha \left[R_n-Q_n\right]\\ & =\alpha R_n+(1-\alpha )Q_n\\ & =\alpha R_n+(1-\alpha )\left[\alpha R_{n-1}+(1-\alpha )Q_{n-1}\right]\\ & =\alpha R_n+(1-\alpha )\alpha R_{n-1}+(1-\alpha {)}^2{Q}_{n-1}\\ & =\alpha R_n+(1-\alpha )\alpha R_{n-1}+(1-\alpha {)}^2\alpha R_{n-2}+\\ & \cdots +(1-\alpha {)}^{n-1}\alpha R_1+(1-\alpha {)}^n{Q}_1\\ & =(1-\alpha {)}^n{Q}_1+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}{R}_i\end{array}\text{\hspace{1em}(2)}$$
我们称（2）式为加权平均，因为权重$(1-\alpha {)}^n+\sum _{i=1}^n\alpha (1-\alpha {)}^{n-i}=1$，其中权重$\alpha (1-\alpha {)}^{n-i}$说明$R_i$的权重取决于它已经过去了多少个，即n-i（how many rewards ago）。若$\alpha <1$，那么当不断有新的$R_n$进来时，$R_i$的权重式不断减小的，具体来说，以$1-\alpha$为基数呈指数级变化。如果$1-\alpha =0$,那么所有权重都聚集到最新的奖励上，其他奖励的权重为0。因此，我们称（2）式代表的学习法则为指数型近期加权平均（exponential recency-weighted average）。

3. 很多时候，步长因子${\alpha }_n(a)$会随着时间步变化。例如在样本平均方法中，${\alpha }_n(a)=\frac{1}{n}$，并且根据大数法则，估计值会收敛到正确值。对于其他变化的 { α n ( a ) } \{\alpha_{n}(a)\} {αn​(a)}收敛性并没有保证。因此我们引入随机逼近理论（stochastic approximation theory） 作为条件来保证估计值以概率$1$收敛：

$$\sum _{n-1}^{\infty }{\alpha }_n(a)and\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty \text{\hspace{1em}(3)}$$
第一个条件保证了步长因子足够大，来克服初始值和震荡；第二个条件保证了步长因子足够小以至于收敛。例如，${\alpha }_n(a)=\frac{1}{n}$是满足收敛条件的，但${\alpha }_n(a)=\alpha$不满足条件二，因此估计值会随着新得到的$R_n$不断变化。实际操作中，满足公式（3）条件的步长因子往往使收敛变得缓慢，所以需要调整，因此，理论分析中，随机逼近理论使用很多，但实际操作中，却不怎么遵守。

4. 练习：
   Ex.2.4. 如果步长因子${\alpha }_n$不是常数，而是随时间步不断变化，那么估计值$Q_n$是过去 { R i } \{R_{i}\} {Ri​}集合的加权平均，它类似于公式（2），请推出用 { R i } \{R_{i}\} {Ri​}表示估计值$Q_n$的具体表达式。
   解：
   $$\begin{array}{rl}{Q}_{n+1}& =Q_n+{\alpha }_n\left[R_n-Q_n\right]\\ & ={\alpha }_n{R}_n+(1-{\alpha }_n)Q_n\\ & ={\alpha }_n{R}_n+(1-{\alpha }_n)\left[{\alpha }_{n-1}{R}_{n-1}+(1-{\alpha }_{n-1})Q_{n-1}\right]\\ & ={\alpha }_n{R}_n+(1-{\alpha }_n){\alpha }_{n-1}{R}_{n-1}+(1-{\alpha }_n)(1-{\alpha }_{n-1})Q_{n-1}\\ & ={\alpha }_n{R}_n+(1-{\alpha }_n){\alpha }_{n-1}{R}_{n-1}+(1-{\alpha }_n)(1-{\alpha }_{n-1}){\alpha }_{n-2}{R}_{n-2}+\\ & \cdots +(1-{\alpha }_n)(1-{\alpha }_{n-1})\cdots (1-{\alpha }_2){\alpha }_1{R}_1\\ & +(1-{\alpha }_n)(1-{\alpha }_{n-1})\cdots (1-{\alpha }_1)Q_1\\ & =\prod _{i=1}^n(1-{\alpha }_i)Q_1+\sum _{i=1}^n\left({\alpha }_i\prod _{j=i+1}^n(1-{\alpha }_j)R_i\right)\end{array}$$
   
   Ex.2.5. 设计并执行一个实验来说明，样本平均方法对不稳定问题的劣势。其中不稳定问题改为增版10臂老虎机问题，即所有真实值$q_{\ast }(a)$开始时一致，之后每一个$q_{\ast }(a)$在每一步都进行独立地随机游走（每加一个正态增量，均值为0，标准差为0.01）。画出对应的动作值形状图，同时考虑另一个常步长因子的估计值方法，其中$\alpha =0.1$。使用$ϵ=0.1$，步数为10000步。

解：这道题一共有两个要求：
一、要求设计一个实验，来表明不稳定性问题对样本平均方法的影响。
二、比较常步长因子（也叫recency-weighted average）和样本平均方法的性状。
要求一：
首先在原来的10-臂老虎机的机制中，已经包含了不稳定性的设计。其中，不稳定性的定义是在每一时间步，真实值$q_{\ast }(t)$是随时间变化的。 如下图所示，问题中叙述的机制是，每次运行会确定$q_{{\ast }^{\prime }}$，这个值不随时间变化。每个时间步都加一个随机采样的值$x$， $x\sim N(0,0.01^2)$，得到$q_{\ast }(t)$作为均值，当前步的奖励$R(t)$采样于$N(q_{\ast }(t),1)$。不可否认这样做增加的不稳定性，但实际上改变的是$R(t)$对应概率分布的标准差，即散度。

下面，我们给一个证明，具体说明这一效果：

命题：上述不稳定机制本质上是加大R(t)分布的标准差，即散度。

证明：

假设$x\sim N(0,c^2)$，则
$$p(x)=N(0,c^2)=\frac{1}{\sqrt{2\pi }c}exp(-\frac{1}{2c^2}{x}^2)\mathrm{d}x$$
同理,记$R(t)$为$r$，则对于给定$x$，$r$采样于一个条件分布，其概率密度函数为
$$p(r|x)=N(x,1^2)=\frac{1}{\sqrt{2\pi }}exp(-\frac{1}{2}{x}^2)\mathrm{d}x$$
我们希望求$r$的概率分布，则$p(r)=\int p(r|x)p(x)\mathrm{d}x$为其分布的概率密度函数。
我们的目标是，得到$p(r)$与$x$无关的精确表达式。
$$\begin{array}{rl}p(r)& =\int p(r|x)p(x)\mathrm{d}x\\ & =\int \frac{1}{\sqrt{2\pi }c}exp\left(-\frac{1}{2c^2}(r-x{)}^2\right)\frac{1}{\sqrt{2\pi }}exp\left(-\frac{1}{2}{x}^2\right)\mathrm{d}x\\ & =\frac{1}{2\pi c}\int exp\left(-\frac{1}{2}\left[(r-x{)}^2+\frac{x^2}{c^2}\right]\right)\mathrm{d}x\\ & =\frac{1}{2\pi c}\int exp\left(-\frac{1}{2}\frac{c^2+1}{c^2}\left(x^2-\frac{2r{c}^2}{c^2+1}x\right)-\frac{r^2}{2}\right)\mathrm{d}x\\ & =\frac{1}{2\pi c}exp\left(-\frac{r^2}{2}\right)\int exp\left(-\frac{1}{2}\frac{c^2+1}{c^2}\left[{\left(x-\frac{r{c}^2}{c^2+1}\right)}^2-{\left(\frac{r{c}^2}{c^2+1}\right)}^2\right]\right)\mathrm{d}x\\ & =\frac{1}{2\pi c}exp\left(-\frac{r^2}{2}\right)exp\left(\frac{c^2+1}{2c^2}\frac{r^2{c}^4}{(c^2+1{)}^2}\right)\int exp\left(-\frac{c^2+1}{2c^2}{\left(x-\frac{r{c}^2}{c^2+1}\right)}^2\right)\mathrm{d}x\\ & =\frac{1}{2\pi c}exp\left(-\frac{r^2}{2(c^2+1)}\right)\int exp\left(-\frac{c^2+1}{2c^2}{x}^2\right)\mathrm{d}x\\ & =\frac{1}{2\pi c}\frac{\sqrt{2}c}{\sqrt{c^2+1}}exp\left(-\frac{r^2}{2(c^2+1)}\right)\int exp\left(-y^2\right)\mathrm{d}y\\ & =\frac{1}{2\pi c}\frac{\sqrt{2}c}{\sqrt{c^2+1}}\sqrt{\pi }exp\left(-\frac{r^2}{2(c^2+1)}\right)\\ & =\frac{1}{\sqrt{2\pi }\sqrt{c^2+1}}exp\left(-\frac{r^2}{2(c^2+1)}\right)\\ & =N(0,(\sqrt{c^2+1}{)}^2)\end{array}$$
其中
$$\boxed{\int exp\left(-y^2\right)\mathrm{d}y=\sqrt{\pi }}$$
$$\boxed{\int exp\left(-a{y}^2\right)\mathrm{d}y=\frac{1}{\sqrt{a}}\int exp\left(-y^2\right)\mathrm{d}y\because lett\doteq \sqrt{a}y}$$
由上可知，对于要求一，原来10-臂老虎机R(t)的标准差为1，已经是不稳定情况了。所以我们的设计应该变化不稳定的剧烈程度，使R(t)的标准差从0，逐步增加到1.5，即[0， 0.5，1，1.5]，观察它对性状图的影响即可。
另外，我们可以从不那么严谨的角去理解：
$$\begin{gathered} \because x\sim N(0,c^2) \\ \because y\sim N(0,1^2) \\ \therefore r\sim N(x,1^2)=x+N(0,1) \\ \sim N(0,c^2)+N(0,1)=N(0,c^2+1) \end{gathered}$$
值得注意，虽然r与x不独立，但正态分布对均值有可加性，可将x分离开，使得到的y与x独立，因此最后的等号成立。

明白机制的本质之后，我们不妨考虑Ｒ(t)分布的总标准差$\sigma =\sqrt{c^2+1}$。记为不稳定因子（nonstationary）。下图是样本平均方法的性状图：

可以看出，面对越不稳定的环境，样本平均方法对于平均值估计的震荡越大；而且找到最佳动作的百分比越低。
要求二、可以看出，对于高度不稳定的10-臂老虎机而言，样本平均的方法比常步长因子的方法效果更好。

具体的代码见我的github博客

疑问： 教材里说，对于不稳定问题，样本平均方法比不上常步长因子方法？为什么我的实验结果不是这样呢？
原因： 因为我的代码里，设的是$ϵ=0.1$，它影响了最终的结果。下面放上$ϵ=0$的效果图：


这样看来，确实教材中的话是正确的。