浅析扩散模型与图像生成【理论篇】（五）——IDDPM

5. IDDPM

  该篇文章《Improved Denoising Diffusion Probabilistic Models》（IDDPM）是对DDPM中存在的问题进行了多方面的改进和试验，显著提升了生成样本的对数似然指标（这是基于似然的图像生成领域最广泛使用的指标之一，表征模型拟合数据分布的能力），使用更少的采样步骤就达到了接近最佳的生成效果。主要做了以下方面的工作：1. 把固定方差改为可学习的方差；2. 提出一种混合损失函数；3. 改进了噪声添加方式；4. 提出一种重要性采样方法提升训练的稳定性；5.提升了采样速度；6. 探究了模型规模和生成样本质量的关系。下面，我们依次介绍一下这几个工作：

5.1 可学习方差

  我们知道在DDPM中，我们只对目标分布的均值进行学习，而方差采用固定值${\beta }_t$或${\tilde{\beta }}_t$。DDPM中的试验表示，如果以FID为评价指标，使用二者作为方差对于生成效果影响不大，而且固定的方差比可学习的方差在训练过程中更加稳定。而本文作者发现，在使用对数似然评价指标时，可学习方差的表现要更好。但由于最佳的方差取值范围非常小，直接使用模型输出方差的确很难训练。因此，作者训练模型输出一个权重向量$v$，对${\beta }_t$和${\tilde{\beta }}_t$进行加权求和，类似在$[{\beta }_t,{\tilde{\beta }}_t]$间进行插值。
$${\Sigma }_{\theta }(x_t,t)=\exp (v\log {\beta }_t+(1-v)\log {\tilde{\beta }}_t)\text{\hspace{1em}(5-1)}$$

5.2 混合损失函数

  由于在DDPM中采用的损失函数$L_{simple}$仅对均值进行监督，而没有对方差进行监督。因此为了保证可学习方差的有效训练，作者提出一种混合损失函数$L_{hybrid}$，将$L_{simple}$与变分下界损失函数$L_{VLB}$进行加权求和
$$L_{hybrid}=L_{simple}+\lambda L_{VLB}\text{\hspace{1em}(5-2)}$$其中$\lambda =0.001$，$L_{simple}$与变分下界损失函数$L_{VLB}$在介绍DDPM的文章中有过详细介绍，此处不再赘述。

5.3 改进噪声时间表（Schedule）

  所谓噪声时间表，其实就是指在扩散阶段添加噪声的方式。我们知道在DDPM中，噪声的权重系数${\bar{\alpha }}_t$是以线性方式变化的，这样做带来的问题是图像会很快就变成纯噪声，导致后面的许多扩散步骤都是无效的，如下图中第一行的图像所示

  为此作者提出一种基于余弦函数的噪声添加方式
$${\bar{\alpha }}_t=\frac{f(t)}{f(0)},f(t)=\cos {\left(\frac{t/T+s}{1+s}\cdot \frac{\pi }{2}\right)}^2\text{\hspace{1em}(5-3)}$$其中，$s=0.008$是一个偏置参数，方式在$t$接近0时，${\beta }_t$的取值太小。改用余弦函数后，扩散过程如上图第二行的图像所示，整个扩散过程变得更加平滑。

5.4 重要性采样

  为了提升生成样本的对数似然指标，理论上直接使用变分下界损失函数$L_{VLB}$要比混合函数$L_{hybrid}$效果更好，但在实际中训练过程却很不稳定，损失存在很大的震荡，如下图所示

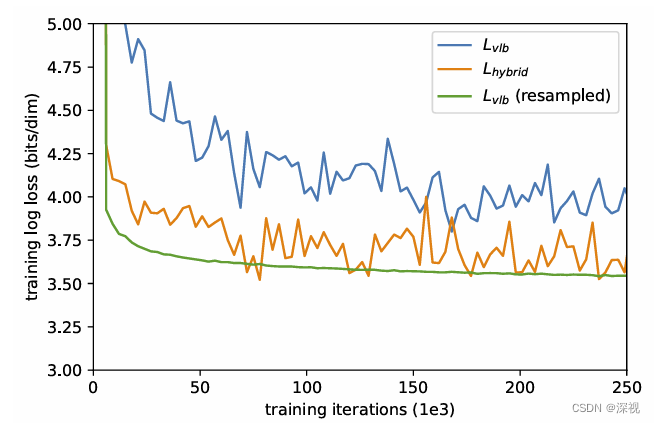
  作者发现这是因为$L_{VLB}$损失的梯度包含太多噪声，而这可能由于训练时随机均匀采样$t$进行训练导致的。我们知道在DDPM中，训练时是从 { 0 , . . . T } \{0,...T\} {0,...T}中均匀随机采样时刻$t$对模型${ϵ}_{\theta }(x_t,t)$进行训练的，且每个时刻的损失权重是相同的。作者提出一种重要性采样方法，给每个时刻$t$的损失$L_t$分配不同的权重$1/p_t$，则损失函数如下
$$L_{VLB}=E_{t\backsim p_t}\left[\frac{L_t}{p_t}\right],\text{where}{p}_t\propto \sqrt{E[L_t^2]}\text{and}\sum p_t=1\text{\hspace{1em}(5-4)}$$由于在训练时$\sqrt{E[L_t^2]}$是未知的，因此作者利用前面10次采样训练的结果来计算$\sqrt{E[L_t^2]}$，并不断更新。在开始训练时，先均匀采样10个时刻$t$用于计算$\sqrt{E[L_t^2]}$。通过重要性采样，$L_{VLB}$损失函数收敛更加平滑且损失更低，如上图所示。但作者发现这一策略对于混合损失函数$L_{hybrid}$并没有显著效果。这种给损失函数增加权重系数的思想，在NCSN和SDE中都有体现。

5.5 加速采样

  类似于DDIM，本文作者也发现由于采用了可学习的方差，可以减少重建过程中的采样步数，实现跨步采样。仅需要100次采样就能达到接近最优结果的采样效果，如下图所示

  作者也与DDIM进行了对比，发现当采样步数少于50时，DDIM的效果更好，当步数超过50时，IDDPM的效果更好。

5.6 模型规模

  最后，作者探究了模型的规模和生成效果之间的关系，作者通过增加网络的通道数来改变模型的规模，试验表明随着模型规模的增大，无论是以对数似然还是FID评价指标，生成效果均呈现一致性的改善。

  至此，我们扩散模型与图像生成【理论篇】的系列文章就告一段落了，后面我将围绕扩散模型在图像生成方面的具体应用，对其中有代表性的文章展开介绍。