向量范数的个人理解

一、范数的概念

        定义：假设是一向量空间，向量的范数是一实函数，若对所有向量和任意一个标量（其中表示实数集或者复数集），下面的公理全部成立：

        1. 非负性：，并且；

        2. 齐次性：对所有复常数都成立；

        3.三角不等式：。

       个人的附加理解：范数是向量空间中一个向量到实数空间中一个实数的映射，而这个映射就是求得一个向量的长度。

       范数与距离的关系：范数也可以认为是一种距离，即向量到零向量的距离。

二、常用的五种范数

        在常见的五种范数中，范数是经常用到的，它通常也被成为欧式范数。当等于时，范数与范数完全等价。另外，范数和范数都是满足非负性、齐次性和三角不等式这三个公理的，你可以通过自己的计算来证明。范数不满足齐次性公理，可以举出一个反例证明其不成立。范数则是范数的极限形式。

三、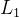和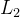范数的三角不等式公理证明思路

        在满足范数的三条公理中，其中前两条都是比较好证明的，但第三条即三角不等式的证明还需要借助巨人的肩膀。

        先说范数吧，这个的话其实就是证明不等式即可，然后推广。而这个不等式的证明很简单，如下：

(1)    

(2)    

        由(1)+(2)得到，，即，，显然。

        而范数你需要借助柯西不等式，如下图所示。在此博客已经证明得非常清楚。

四、结束语

        以上均是我的个人总结和理解，如有遗漏或出错，欢迎提出留言批评改正。

参考资料

1. 张贤达，《矩阵分析与应用》第2版。

2. 百度百科，绝对值不等式。