使用PyTorch计算中位数/中值

一、中位数(【统计学】专有名词)

        中位数(Median)又称中值，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合划分为相等的上下两部分。对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，通常取最中间的两个数值的平均数作为中位数。

        其他类似的概念：众数和平均数。

        众数：众数（Mode）是指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。 也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。用M表示。一般来说，一组数据中，出现次数最多的数就叫这组数据的众数。例如：1，2，3，3，4的众数是3。但是，如果有两个或两个以上个数出现次数都是最多的，那么这几个数都是这组数据的众数。例如：1，2，2，3，3，4的众数是2和3。还有，如果所有数据出现的次数都一样，那么这组数据没有众数。例如：1，2，3，4，5没有众数。

        平均数：平均数，统计学术语，是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。平均数又称均值。计算公式：(a1+a2+...+an)/n。

二、中位数、众数、平均数的直观区别

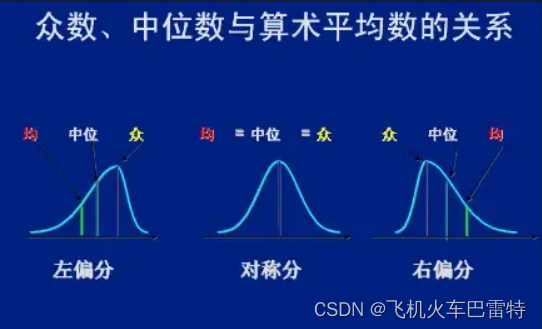
三、第一种计算方式

        利用torch.median()方法计算，代码

import torch

a = torch.tensor([10, 10, 40, 20, 70, 40, 20, 50, 50, 70], dtype=torch.float)
b = torch.tensor([10, 20, 30, 40, 50, 60], dtype=torch.float)
c = torch.tensor([10, 20, 30, 40, 50], dtype=torch.float)

print(a.sort().values, a.median().item())
print(b.sort().values, b.median().item())
print(c.sort().values, c.median().item())

        输出

tensor([10., 10., 20., 20., 40., 40., 50., 50., 70., 70.]) 40.0
tensor([10., 20., 30., 40., 50., 60.]) 30.0
tensor([10., 20., 30., 40., 50.]) 30.0

        在观察值为偶数的情况下，将返回两个中位数中的较低值。

四、第二种计算方式

        利用torch.quantile()方法计算，代码

import torch

a = torch.tensor([10, 10, 40, 20, 70, 40, 20, 50, 50, 70], dtype=torch.float)
b = torch.tensor([10, 20, 30, 40, 50, 60], dtype=torch.float)
c = torch.tensor([10, 20, 30, 40, 50], dtype=torch.float)

print(a.sort().values, a.quantile(q=0.5).item())
print(b.sort().values, b.quantile(q=0.5).item())
print(c.sort().values, c.quantile(q=0.5).item())

        输出

tensor([10., 10., 20., 20., 40., 40., 50., 50., 70., 70.]) 40.0
tensor([10., 20., 30., 40., 50., 60.]) 35.0
tensor([10., 20., 30., 40., 50.]) 30.0

        在观察值为偶数的情况下，将返回两个中位数中的平均值。

五、参考

        中位数_百度百科

        torch.median

        torch.quantile