基于python的九轴惯性传感器的数据预处理代码-中值滤波实验

**

基于python的九轴惯性传感器的数据预处理代码-中值滤波实验

**
import random
import numpy as np
import pandas as pd
import scipy.signal as signal
import matplotlib.pyplot as plt
import time

#导入传感器的9列数据
f=pd.read_csv(“G:/桌面文件/传感器数据1.csv”,usecols=[1,2,3,4,5,6,7,8,9])

ax1=f[“ax”].values
ay1=f[“ay”].values*(-1)
az1=f[“az”].values

mx1=f[“mx”].values
my1=f[“my”].values
mz1=f[“mz”].values

gx1=f[“gx”].values
gy1=f[“gy”].values
gz1=f[“gz”].values

#原始数据除以对应的灵敏度

x1=ax1/16384
x2 =ay1/16384
x3=az1/16384

x4=gx1/16.4
x5=gy1/16.4
x6=gz1/16.4

x7=mx1/0.6
x8=my1/0.6
x9=mz1/0.6

print(“gyrX原始数据的方差：”)
arr_var1 = np.var(x1)
print(arr_var1)

#d=cv2.blur(x,10)
d1=signal.medfilt(x1,11) #一维中值滤波
d2=signal.medfilt(x2,11)
d3=signal.medfilt(x3,11)

d4=signal.medfilt(x4,11)
d5=signal.medfilt(x5,11)
d6=signal.medfilt(x6,11)

d7=signal.medfilt(x7,11)
d8=signal.medfilt(x8,11)
d9=signal.medfilt(x9,11)

#中值滤波后数据的方差
print(“ax中值滤波数据的方差：”)
arr_var2 = np.var(d1)
print(arr_var2)

print(“ay中值滤波数据的方差：”)
arr_var2 = np.var(d2)
print(arr_var2)

print(“az中值滤波数据的方差：”)
arr_var2 = np.var(d3)
print(arr_var2)

print(“gx中值滤波数据的方差：”)
arr_var2 = np.var(d4)
print(arr_var2)

print(“gy中值滤波数据的方差：”)
arr_var2 = np.var(d5)
print(arr_var2)

print(“gz中值滤波数据的方差：”)
arr_var2 = np.var(d6)
print(arr_var2)

print(“mx中值滤波数据的方差：”)
arr_var2 = np.var(d7)
print(arr_var2)

print(“my中值滤波数据的方差：”)
arr_var2 = np.var(d8)
print(arr_var2)

print(“mz中值滤波数据的方差：”)
arr_var2 = np.var(d9)
print(arr_var2)

#图形绘制

x0=list(range(len(x1)))

plt.figure(1)
plt.subplot(311)

#d1.axis.set_major_locator(MultipleLocator(10))

plt.plot(x0,x1,c=“r”,label=“original”)
plt.plot(x0,d1,c=“blue”,label=“revised”)
plt.title(“middle-ax”,fontsize=10,fontname=“Times New Roman”)#标题

plt.subplot(312)
plt.plot(x0,x2,c=“r”,label=“original”)
plt.plot(x0,d2,c=“blue”,label=“revised”)
plt.title(“middle-ay”,fontsize=10,fontname=“Times New Roman”)#标题

plt.subplot(313)
plt.plot(x0,x3,c=“r”,label=“original”)
plt.plot(x0,d3,c=“blue”,label=“revised”)
plt.title(“middle-az”,fontsize=10,fontname=“Times New Roman”)#标题
plt.tight_layout()

plt.figure(2)
plt.subplot (311)
plt.plot(x0,x4,c=“r”,label=“original”)
plt.plot(x0,d4,c=“blue”,label=“revised”)
plt.title(“middle-gx”,fontsize=14,fontname=“Times New Roman”)#标题

plt.subplot(312)
plt.plot(x0,x5,c=“r”,label=“original”)
plt.plot(x0,d5,c=“blue”,label=“revised”)
plt.title(“middle-gy”,fontsize=14,fontname=“Times New Roman”)#标题

plt.subplot (313)
plt.plot(x0,x6,c=“r”,label=“original”)
plt.plot(x0,d6,c=“blue”,label=“revised”)
plt.title(“middle-gz”,fontsize=14,fontname=“Times New Roman”)#标题
plt.tight_layout()

plt.figure(3)
plt.subplot (311)
plt.plot(x0,x7,c=“r”,label=“original”)
plt.plot(x0,d7,c=“blue”,label=“revised”)
plt.title(“middle-mx”,fontsize=14,fontname=“Times New Roman”)#标题

plt.subplot (312)
plt.plot(x0,x8,c=“r”,label=“original”)
plt.plot(x0,d8,c=“blue”,label=“revised”)
plt.title(“middle-my”,fontsize=14,fontname=“Times New Roman”)#标题

plt.subplot(313)
plt.plot(x0,x9,c=“r”,label=“original”)
plt.plot(x0,d9,c=“blue”,label=“revised”)
plt.title(“middle-mz”,fontsize=14,fontname=“Times New Roman”)#标题
plt.tight_layout()
plt.legend()
plt.show()

实验结果如下：

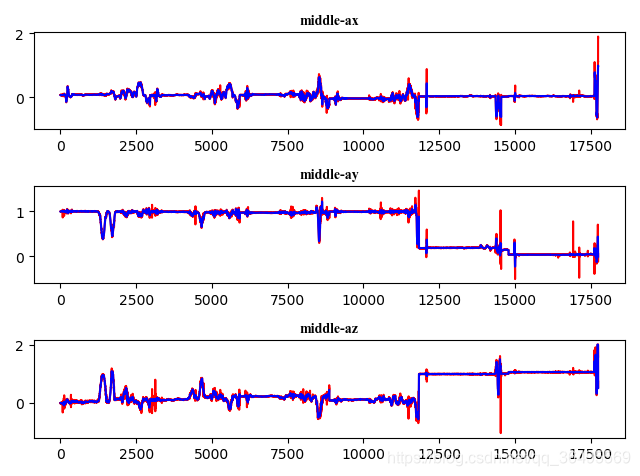
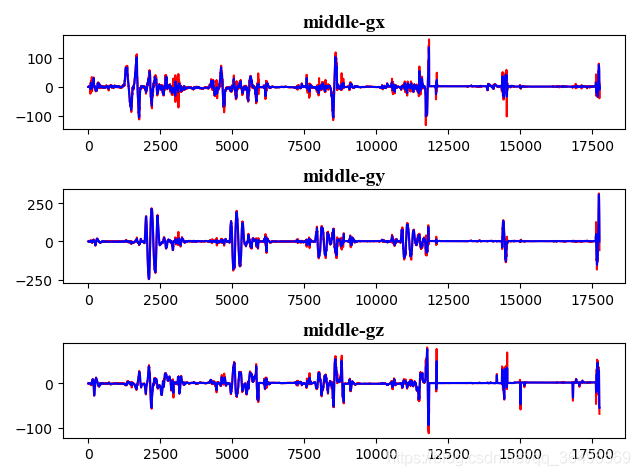
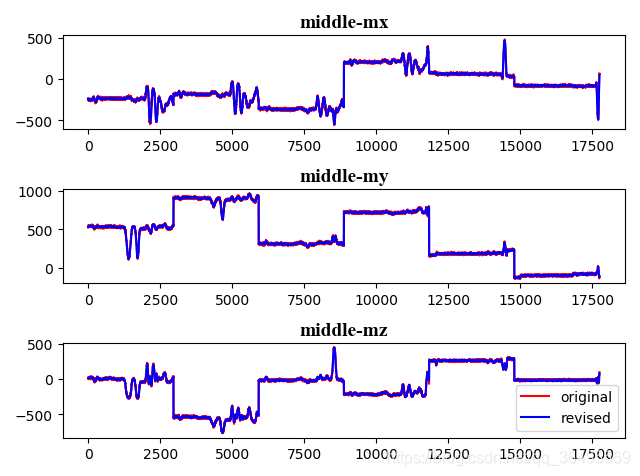
由于本人python还在学基础阶段，所以代码写的很一般，也很直白，希望能够一起交流关于姿态解算，传感器标定等问题，欢迎指导，我在不断改进。