考研对信息的获取至关重要，此公众号会发表计算机考研（初复试信息）、夏令营等资料，方便考研人对信息的获取，节约自身查找资料的时间
目录
1. SVM
支持向量机（support vector machines，SVM）是一种二分类模型，它将实例的特征向量映射为空间中的一些点，SVM 的目的就是想要画出一条线，以 “最好地” 区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。
SVM 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出，目前的版本（soft margin）是由 Corinna Cortes 和 Vapnik 在1993年提出，并在1995年发表。深度学习（2012）出现之前，SVM 被认为机器学习中近十几年来最成功，表现最好的算法。
1.1 SVM 基本概念
将实例的特征向量（以二维为例）映射为空间中的一些点，如下图的实心点和空心点，它们属于不同的两类。SVM 的目的就是想要画出一条线，以“最好地”区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。
Q1：能够画出多少条线对样本点进行区分？
答：线是有无数条可以画的，区别就在于效果好不好，每条线都可以叫做一个划分超平面。比如上面的绿线就不好，蓝线还凑合，红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。
Q2：为什么要叫作“超平面”呢？
答：因为样本的特征很可能是高维的，此时样本空间的划分就不是一条线了。
Q3：画线的标准是什么？/ 什么才叫这条线的效果好？/ 哪里好？
答：SVM 将会寻找可以区分两个类别并且能使间隔（margin）最大的划分超平面。比较好的划分超平面，样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。
Q4：间隔（margin）是什么？
答：对于任意一个超平面，其两侧数据点都距离它有一个最小距离（垂直距离），这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin，虚线是由距离中央实线最近的两个点所确定出来的（也就是由支持向量决定）。但此时 margin 比较小，如果用第二种方式画，margin 明显变大也更接近我们的目标。
Q5：为什么要让 margin 尽量大？
答：因为大 margin 犯错的几率比较小，也就是更鲁棒啦。
Q6：支持向量是什么？
答：从上图可以看出，虚线上的点到划分超平面的距离都是一样的，实际上只有这几个点共同确定了超平面的位置，因此被称作 “支持向量（support vectors）”，“支持向量机” 也是由此来的。
2寻找最大间隔
2.1点到超平面的距离公式
既然这样的直线是存在的，那么我们怎样寻找出这样的直线呢？与二维空间类似，超平面的方程也可以写成一下形式：
（1.1）
有了超平面的表达式之后之后，我们就可以计算样本点到平面的距离了。假设
为样本的中的一个点，其中
表示为第个特征变量。那么该点到超平面的距离
就可以用如下公式进行计算：
（1.2）
其中||W||为超平面的范数，常数b类似于直线方程中的截距。
上面的公式可以利用解析几何或高中平面几何知识进行推导，这里不做进一步解释。
2.2最大间隔的优化模型
现在我们已经知道了如何去求数据点到超平面的距离，在超平面确定的情况下，我们就能够找出所有支持向量，然后计算出间隔margin。每一个超平面都对应着一个margin，我们的目标就是找出所有margin中最大的那个值对应的超平面。因此用数学语言描述就是确定w、b使得margin最大。这是一个优化问题其目标函数可以写成：
（1.3）
其中
表示数据点的标签，且其为-1或1。距离用
计算，这是就能体会出-1和1的好处了。如果数据点在平面的正方向(即+1类)那么是一个正数，而当数据点在平面的负方向时(即-1类)，依然是一个正数，这样就能够保证始终大于零了。注意到当w和b等比例放大时，d的结果是不会改变的。因此我们可以令所有支持向量的u为1，而其他点的u大1这是可以办通过调节w和b求到的。因此上面的问题可以简化为： 
（1.4）
为了后面计算的方便，我们将目标函数等价替换为：
（1.5）
这是一个有约束条件的优化问题，通常我们可以用拉格朗日乘子法来求解。拉格朗日乘子法的介绍可以参考这篇博客。应用拉格朗日乘子法如下：
令 
（1.6）
求L关于求偏导数得：
（1.7）
将(1.7)代入到(1.6)中化简得：
（1.8）
原问题的对偶问题为：
（1.9）
该对偶问题的KKT条件为
（1.10）
到此，似乎问题就能够完美地解决了。但是这里有个假设：数据必须是百分之百可分的。但是实际中的数据几乎都不那么“干净”，或多或少都会存在一些噪点。为此下面我们将引入了松弛变量来解决这种问题。
2.3松弛变量
由上一节的分析我们知道实际中很多样本数据都不能够用一个超平面把数据完全分开。如果数据集中存在噪点的话，那么在求超平的时候就会出现很大问题。从图三中课看出其中一个蓝点偏差太大，如果把它作为支持向量的话所求出来的margin就会比不算入它时要小得多。更糟糕的情况是如果这个蓝点落在了红点之间那么就找不出超平面了。
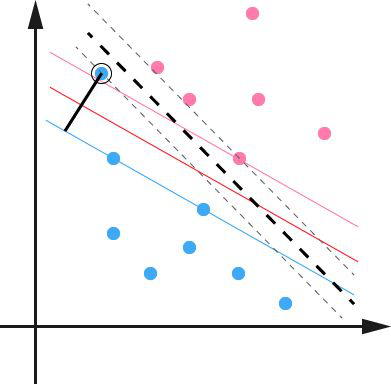
图 3
因此引入一个松弛变量ξ来允许一些数据可以处于分隔面错误的一侧。这时新的约束条件变为:
（1.11）
式中ξi的含义为允许第i个数据点允许偏离的间隔。如果让ξ任意大的话，那么任意的超平面都是符合条件的了。所以在原有目标的基础之上，我们也尽可能的让ξ的总量也尽可能地小。所以新的目标函数变为：
（1.12）
（1.13）
其中的C是用于控制“最大化间隔”和“保证大部分的点的函数间隔都小于1”这两个目标的权重。将上述模型完整的写下来就是：
（1.14）
新的拉格朗日函数变为：
（1.15）
接下来将拉格朗日函数转化为其对偶函数，首先对
分别求
ξ的偏导，并令其为0,结果如下：
（1.16）
代入原式化简之后得到和原来一样的目标函数：
（1.17）
但是由于我们得到
而
，因此有
所以对偶问题写成：
（1.18）
经过添加松弛变量的方法，我们现在能够解决数据更加混乱的问题。通过修改参数C，我们可以得到不同的结果而C的大小到底取多少比较合适，需要根据实际问题进行调节。
3.核函数
机器学习算法中，不论是感知机还是支持向量机，在面对非线性问题时，往往都会用到一个名为“核函数”的技巧。那么到底什么是核函数呢？是否真的如听起来这样难以理解呢？
核函数：是映射关系
的内积，映射函数本身仅仅是一种映射关系，并没有增加维度的特性，不过可以利用核函数的特性，构造可以增加维度的核函数，这通常是我们希望的。
二维映射到三维，区分就更容易了，这是聚类、分类常用核函数的原因。为什么PCA这样一个降维算法也用核函数呢？
左图为原数据，右图为映射到三维的数据，可以看出：同样是降到1维，先通过Kernel映射到（Kernel是映射的内积，不要弄乱了）三维，再投影到1维，就容易分离开，这就是Kernel在PCA降维中的应用，本质还是对原有数据增加维度。
下面是李航的《统计学习方法》中对于核函数的定义：
要注意，核函数和映射没有关系。核函数只是用来计算映射到高维空间之后的内积的一种简便方法。
一般英文文献对Kernel有两种提法，一是Kernel Function，二是Kernel Trick。从Trick一词中就可以看出，这只是一种运算技巧而已，不涉及什么高深莫测的东西。
具体巧在哪里呢？我们如果想进行原本就线性不可分的数据集进行分割，那么选项一是容忍错误分类，即引入Soft Margin；选项二是我们可以对Input Space做Feature Expansion，把数据集映射到高维中去，形成了Feature Space。我们几乎可以认为（引用Caltech的课堂用语“We are safe but not certain”）原本在低维中线性不可分的数据集在足够高的维度中存在线性可分的超平面。
那么这种非线性可分的数据是否就不能用svm算法来求解呢？答案是否定的。事实上，对于低维平面内不可分的数据，放在一个高维空间中去就有可能变得可分。以二维平面的数据为例，我们可以通过找到一个映射将二维平面的点放到三维平面之中。理论上任意的数据样本都能够找到一个合适的映射使得这些在低维空间不能划分的样本到高维空间中之后能够线性可分。我们再来看一下之前的目标函数：
（1.19）
定义一个映射使得将所有映射到更高维空间之后等价于求解上述问题的对偶问题：
（1.20）
这样对于线性不可分的问题就解决了，现在只需要找出一个合适的映射即可。当特征变量非常多的时候在，高维空间中计算内积的运算量是非常庞大的。考虑到我们的目的并不是为找到这样一个映射而是为了计算其在高维空间的内积，因此如果我们能够找到计算高维空间下内积的公式，那么就能够避免这样庞大的计算量，我们的问题也就解决了。实际上这就是我们要找的核函数
，即两个向量在隐式映射后的空间中的内积。下面的一个简单例子可以帮助我们更好地理解核函数。
通过以上例子，我们可以很明显地看到核函数是怎样运作的。上述问题的对偶问题可以写成如下形式：
（1.21）
那么怎样的函数才可以作为核函数呢？下面的一个定理可以帮助我们判断。
Mercer定理：任何半正定的函数都可以作为核函数。其中所谓半正定函数
是指拥有训练集数据集合，我们定义一个矩阵的元素
，这个矩阵是
的矩阵，如果这个矩阵是半正定的，那么
就称为半正定函数。
值得注意的是，上述定理中所给出的条件是充分条件而非充要条件。因为有些非正定函数也可以作为核函数。
下面是一些常用的核函数：
表1 常用核函数表
| 核函数名称 | 核函数表达式 | 核函数名称 | 核函数表达式 |
| 线性核 |
| 指数核 |
|
| 多项式核 |
| 拉普拉斯核 |
|
| 高斯核 |
| Sigmoid核 |
|
现在我们已经了解了一些支持向量机的理论基础，我们通过对偶问题的的转化将最开始求
的问题转化为求
的对偶问题。只要找到所有的(即找出所有支持向量)，我们就能够确定
。然后就可以通过计算数据点到这个超平面的距离从而判断出该数据点的类别。
4.相关概念补充
4.1线性可区分和线性不可区分
能够用一条直线对样本点进行分类的属于线性可区分（linear separable），否则为线性不可区分（linear inseparable)。
以下三个例子，都是线性不可区分的，即无法用一条直线将两类样本点区分开。
而刚才的例子就是线性可区分的。
思考问题：
- 如何选择合理的非线性转化把数据转到高维空间中？
- 如何解决计算内积时算法复杂度非常高的问题？
使用核方法（kernel trick)
4.2对偶问题
对偶问题是实质相同但从不同角度提出不同提法的一对问题。对偶现象是许多管理与工程实际中存在的一种普遍现象。例如，企业怎样充分利用现有人力、物力去完成更多的任务和怎样用最少的人力、物力消耗去完成给定的任务，就是互为对偶的一对问题。对偶理论是从数量关系上研究这些对偶问题的性质、关系及其应用的理论和方法。每一个线性规划问题，都存在一个与之相联系的对偶问题。
4.3SVM 可扩展到多分类问题
SVM 扩展可解决多个类别分类问题：
对于每个类，有一个当前类和其他类的二类分类器（one-vs-rest）
将多分类问题转化为 n 个二分类问题，n 就是类别个数。
4.4SVM 算法特性
- 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以 SVM 不太容易产生 overfitting。
- SVM 训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。
- 一个 SVM 如果训练得出的支持向量个数比较少，那么SVM 训练出的模型比较容易被泛化。
8万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
