秋招总结帖，还愿牛客

秋招总结帖

待完善，持续更新

小米（offer）

寒武纪（池子）

荣耀（二面挂）

华为（池子）

茄子科技（hr面后挂）

58 同城（意向）

经纬恒润（天津，n+2w）

海信（青岛，nw）

XX（北京国企，有京户，nw）

神策数据（三面挂）

招银网络科技（一面鸽）

小红书（一面挂）

快手（一面挂）

字节跳动（一面挂）

百度（一面挂）

oppo（一面挂）

龙湖科技（一面挂）

笔试挂或无后续

京东

美团

哔哩哔哩

拼多多

网易

携程

奇安信

虾皮

蔚来

知乎

图森

海量数据处理

• 可以全部放到内存：哈希表统计
• 不可以全部放到内存：哈希（字典树也可用于统计次数），取模，映射到小文件（一个query只会出现在一个文件里）
• TOP K 问题：最小堆（平均 lgK 时间复杂度），归并排序
• bitMap

机器学习算法

• 特征工程基本操作

  • 连续特征归一化，类别特征表示
  • 特征表示
  • 特征选择
  • 特征去噪

• XGboost要点

  • 基模型都是回归树
  • 一般用 CART，CART 一般是二叉树，所以对于多类别的离散特征，需要编码（one-hot encoding 或者 label encoding）
  • 对于多类别离散特征的处理，
    • 存在大小关系的按照连续特征处理；
    • 不存在大小关系的，特征捆绑（city == beijing || city == shanghai），编码，embedding

• 介绍一下 GBDT

• XGBoost 常调的参数

• SVM 为什么进行对偶变化

  • 对偶问题容易求解：
    • 极小问题变成了极大极小问题
  • 自然引入核函数
  • 推导步骤
    • 最大间隔
    • 约束优化问题 -> 拉格朗日函数(极小极大问题) -> 对偶变化，变为极大极小问题
    • L(w, b, a)分别对 w, b 求导并令导数为 0，得到 a 和 w, b 的关系，代入L(w, b, a)，极大极小问题变成了关于 a 的极小问题，可证明此极小问题与原极大极小问题等价
    • 解上述问题，求得 a， 利用 KKT 条件求 w, b
    • 得到分类决策函数

• 贝叶斯概率计算

• t-SNE 和 PCA

  • 样本主成分

    • 给定样本矩阵 $X$。样本第一主成分 $y_1=a_1^T\mathbf{x}$ 是在 $a_1^T{a}_1=1$ 条件下，使得 $a_1^T{x}_j(j=1,2,...,n)$ 的样本方差 $a_1^{T}S{a}_1$ 最大的 $x$ 的线性变换；
    • 样本第二主成分 $y_2=a_2^T\mathbf{x}$ 是在 $a_2^T{a}_2=1$ 和 $a_2^T{x}_j$ 与 $a_1^T{x}_j(j=1,2,..,n)$ 的样本协方差 $a_1^{T}S{a}_2=0$ 条件下，使得 $a_2^T{x}_j$ 的样本方差 $a_2^{T}S{a}_2$ 最大的 $x$ 的线性变换；
    • 一般地，样本第 i 主成分 $y_i=a_i^{T}x$ 是在 $a_i^T{a}_i=1$ 和 $a_i^T{x}_j$ 与 $a_k^T{x}_j(k<i,j=1,2,...,n)$ 的 样本协方差 $a_k^{T}S{a}_i=0$ 条件下使得 $a_i^T{x}_j$ 的样本方差 $a_i^{T}S{a}_i$ 最大的 $x$ 的线性变换。

  • PCA 推导： 设 $x$ 是 m 维随机向量，$\Sigma$ 是 $x$ 的协方差矩阵 ($\mu =E(x),\Sigma =E[(x-\mu )(x-\mu {)}^T]$)，$\Sigma$ 的特征值分别是 ${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_m\ge 0$，特征值对应的单位特征向量分别是 ${\alpha }_1,{\alpha }_2,...,{\alpha }_m$，则 $x$ 的第 k 主成分是

  $$y_k={\alpha }_k^{T}x={\alpha }_{1k}{x}_1+{\alpha }_{2k}{x}_2+...+{\alpha }_{mk}{x}_m,k=1,2,...,m$$

  ​ $x$ 第 k 主成分的方差是
  $$var(y_k)={\alpha }_k^T\Sigma {\alpha }_k={\lambda }_k,k=1,2,...,m$$
  ​ 即协反差矩阵的第 k 个特征值。

  ​ **证明：**采用拉格朗日乘子法求出主成分。

  ​ 首先求 $x$ 的第一主成分 $y_1={\alpha }_1^{T}x$，即求系数向量 ${\alpha }_1$。第一主成分是在 ${\alpha }_1^T{\alpha }_1=1$ 条件下，$x$ 的所有线性变换中使方差 $var({\alpha }_1^{T}x)$ 达到最大的。

  ​ 求第一主成分就是求解约束最优化问题：
  $$\begin{gathered} \underset{{\alpha }_1}{\max }{\alpha }_1^T\Sigma {\alpha }_1 \\ s.t.{\alpha }_1^T{\alpha }_1=1 \end{gathered}$$
  定义拉格朗日函数：
  $$L({\alpha }_1,\lambda )={\alpha }_1^T\Sigma {\alpha }_1-\lambda ({\alpha }_1^T{\alpha }_1-1)$$
  其中 $\lambda$ 是拉格朗日乘子。将拉格朗日函数对 ${\alpha }_1$ 求导，并令其为 0，得
  $$\Sigma {\alpha }_1-\lambda {\alpha }_1=0$$
  因此，$\lambda$ 是 $\Sigma$ 的特征值，${\alpha }_1$ 是对应的单位特征向量。于是，目标函数
  $${\alpha }_1^T\Sigma {\alpha }_1={\alpha }_1^T\lambda {\alpha }_1=\lambda$$
  假设 ${\alpha }_1$ 是 $\Sigma$ 的最大特征值 ${\lambda }_1$ 对应的单位特征向量，显然 ${\alpha }_1$ 与 ${\lambda }_1$ 是最优化问题的解。所以，${\alpha }_1^{T}x$ 构成第一主成分，其方差是协方差矩阵的最大特征值。

  ​ 接着求 $x$ 的第二主成分 $y_2={\alpha }_2^{T}x$。第二主成分的 ${\alpha }_2$ 是在 ${\alpha }_2^T{\alpha }_2=1$，且 ${\alpha }_2^{T}x$ 与 ${\alpha }_1^{T}x$ 不相关的条件下，$x$ 的所有线性变换使方差 $var({\alpha }_2^{T}x)={\alpha }_2^T\Sigma {\alpha }_2$ 达到最大的。

  求解第二主成分需要求解约束优化问题
  $$\begin{gathered} \underset{{\alpha }_2}{\max }{\alpha }_2^T\Sigma {\alpha }_2 \\ s.t.{\alpha }_1^T\Sigma {\alpha }_2=0,{\alpha }_2^T\Sigma {\alpha }_1=0 \\ {\alpha }_2^T{\alpha }_2=1 \end{gathered}$$
  注意到
  $$\begin{gathered} {\alpha }_1^T\Sigma {\alpha }_2={\alpha }_2^T\Sigma {\alpha }_1={\alpha }_2^T{\lambda }_1{\alpha }_1={\lambda }_1{\alpha }_2^T{\alpha }_1={\lambda }_1{\alpha }_1^T{\alpha }_2 \\ 且{\alpha }_1^T{\alpha }_2={\alpha }_2^T{\alpha }_1=0 \end{gathered}$$
  定义拉格朗日函数
  $${\alpha }_2^T\Sigma {\alpha }_2-\lambda ({\alpha }_2^T{\alpha }_2-1)-\varphi {\alpha }_2^T{\alpha }_1$$
  其中，$\lambda ,\varphi$ 是拉格朗日乘子。对 ${\alpha }_2$ 求导，并令其为 0，得
  $$2\Sigma {\alpha }_2-2\lambda {\alpha }_2-\varphi {\alpha }_1=0$$
  左乘 ${\alpha }_1^T$ ，有
  $$2{\alpha }_1^T\Sigma {\alpha }_2-2\lambda {\alpha }_1^T{\alpha }_2-\varphi {\alpha }_1^T{\alpha }_1=0$$
  由于约束条件，上式前两项是 0，且 ${\alpha }_1^T{\alpha }_1=1$ ，得出 $\varphi =0$ ，因此
  $$\Sigma {\alpha }_2-\lambda {\alpha }_2=0$$
  由此，$\lambda$ 是 $\Sigma$ 的特征值，${\alpha }_2$ 是对应的特征向量。于是，目标函数
  $${\alpha }_2^T\Sigma {\alpha }_2={\alpha }_2^T\lambda {\alpha }_2=\lambda {\alpha }_2^T{\alpha }_2=\lambda$$
  $\Sigma$ 的第二大特征值 ${\lambda }_2$ 显然是以上最优化问题的解。于是 ${\alpha }_2^{T}x$ 构成第二主成分，其方差等于协方差矩阵的第二大特征值，
  $$var({\alpha }_2^{T}x)={\alpha }_2^T\Sigma {\alpha }_2={\lambda }_2$$
  一般地，$x$ 的第 $k$ 主成分是 ${\alpha }_k^{T}x$，并且 $var({\alpha }_k^{T}x)={\lambda }_k$，其中，${\lambda }_k$ 是 $\Sigma$ 的第 $k$ 个特征值，${\alpha }_k$ 是对应的特征向量。

  总体主成分的性质：

  (1) 总体主成分 $y$ 的协方差矩阵是对角矩阵：$cov(y)=\Lambda =diag({\lambda }_1,{\lambda }_2,...,{\lambda }_m)$;

  (2) 总体主成分 $y$ 的方差之和等于随机变量 $x$ 的方差之和；

  (3) 第 k 个主成分 $y_k$ 与变量 $x_i$ 的相关系数 $\rho (y_k,x_i)$ 称为因子负荷量（factor loading）,它表示第 k 个主成分 $y_k$ 与变量 $x_i$ 的相关关系。计算公式是
  $$\begin{gathered} \rho (y_k,x_i)=\frac{cov(y_k,x_i)}{\sqrt{var(y_k)var(x_i)}}=\frac{cov({\alpha }_k^{T}x,e_i^{T}x)}{\sqrt{{\lambda }_k}\sqrt{{\sigma }_{ii}}} \\ cov({\alpha }_k^{T}x,e_i^{T}x)={\alpha }_k^T\Sigma e_i=e_i^T\Sigma {\alpha }_k={\lambda }_k{e}_i^T{\alpha }_k={\lambda }_k{\alpha }_{ik} \\ \rho (y_k,x_i)=\frac{{\lambda }_k{\alpha }_{ik}}{\sqrt{{\lambda }_k}\sqrt{{\sigma }_{ii}}}=\frac{\sqrt{{\lambda }_k}{\alpha }_{ik}}{\sqrt{{\sigma }_{ii}}} \end{gathered}$$
  (4) 第 k 个主成分 $y_k$ 与 m 个变量的因子负荷量满足
  $$\sum _{i=1}^m{\sigma }_{ii}{\rho }^2(y_k,x_i)={\lambda }_k$$
  (5) m 个主成分与第 i 个变量 $x_i$ 的因子负荷量满足
  $$\sum _{k=1}^m{\rho }^2(y_k,x_i)=1$$

• 逻辑回归：二项的逻辑回归是如下的条件概率分布：

$$\begin{gathered} P(Y=1|x)=\frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)} \\ P(Y=0|x)=\frac{1}{1+exp(w\cdot x+b)} \end{gathered}$$

一个事件的几率 (odds) 是指该事件的概率与该事件不发生的概率的比值。如果事件发生的概率是 p，那么事件的几率是$\frac{p}{1-p}$ ，对于逻辑回归而言，该事件的对数几率是输入 $x$ 的线性函数表示的模型：
$$log\frac{P(Y=1|x)}{1-P(Y=1|x)}=w\cdot x$$
参数估计：

设：
$$P(Y=1|x)=\pi (x),P(Y=0|x)=1-\pi (x)$$
似然函数为
$$\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i}$$
对数似然函数为
KaTeX parse error: No such environment: align at position 16: {align} \begin{̲a̲l̲i̲g̲n̲}̲ L(w)&=\sum_{i=…
对 $L(w)$ 求极大值，得到 $w$ 的估计值。对对数似然函数取负转化为极小化问题，利用梯度下降法求解：
$$-\frac{\partial L(w)}{\partial w}=\sum _{i=1}^N[-y_i{x}_i+\frac{x_{i}exp(w\cdot x_i)}{1+exp(w\cdot x_i)}]=-\sum _{i=1}^N{x}_i[y_i-h_w(x_i)]$$
梯度更新公式：
$$w_{n+1}=w_n+\eta \cdot \left(\frac{\partial L(w)}{\partial w}\right)=w_n+\eta \cdot \sum _{i=1}^N{x}_i[y_i-h_w(x_i)]$$
其中，$\eta$ 是学习率。

• 梯度下降算法求解极大似然过程（更新过程）

• 逻辑回归为什么不使用平方损失

  若使用平方损失，损失函数为

$$L(w)=\frac{1}{N}\sum _{i=1}^N[y_i-h_w(x_i){]}^2$$

极小化损失函数，利用梯度下降法求解：
$$\frac{\partial L(w)}{\partial w}=-\frac{2}{N}\sum _{i=1}^N{x}_i[y_i-h_w(x_i)]h_w^{\prime }(x_i)=-\frac{2}{N}\sum _{i=1}^N{x}_i[y_i-h_w(x_i)]\frac{exp(w\cdot x_i)}{[1+exp(w\cdot x_i){]}^2}$$
当 $w\cdot x_i$ 过大或过小时，$h_w^{\prime }(x_i)$ 都很小，会导致梯度消失的问题。

• PCA

  • 最大化投影方差

• K-means 和 DBSCAN: Density-Based Spatial Clustering Algorithm with Noise

  • k-means
    • 聚类效果依赖于簇心的选择
    • 会把所有数据点聚类，对离群点不敏感
    • 对每个簇来说，所有的方向同等重要，仅适合球形数据簇
  • DBSCAN
    • 优点：
      • 不需要指定簇数
      • 适合各种复杂形状的数据点分布
      • 可识别出不属于任何簇的离群点
    • 缺点：
      • 运行速度慢
      • 参数调整，
      • 对于具有不同密度的簇，效果不好

• 聚类算法

  • K-Means
  • 手肘法，复杂度，优缺点
    • 手肘法：SSE(误差平方和和 K 值的曲线，选曲率最大的地方)
  • 层次聚类
  • DBSCAN
  • …

• GBDT 和 XGBoost

  • GBDT 是机器学习算法，XBGoost 是工程实现
  • XGBoost 在基分类器显示加入正则化项，控制模型复杂度，有利于防止过拟合，一个是限制树的高度，一个是叶子节点权重的二范数
  • XGBoost 同时使用对损失函数做二阶泰勒展开，可以更快更准的降低偏差
  • XGBoost 支持多种基分类器
  • 支持对数据采样，类似于随机森林（特征采样，样本采样），降低方差
  • 处理缺失值，分裂时尝试把空缺值当成一类数据分到左节点或右节点，选增益大的

• XGBoost 和 lightGBM

  • XGBoost 采用预排序，对节点的特征进行预排序并遍历选择最优分割点，数据量大时贪心耗时，lightGBM 使用直方图
  • lightGBM 对样本基于梯度采样
  • XGBoost 是 level-wise，lightGBM 是 leaf-wise
  • 互斥特征捆绑

• bagging 和 boosting 方法的区别

  • bagging 对训练集进行有放回抽样，boosting 对分类错误的样本加权以降低偏差
  • bagging 主要关注降低方差，boosting 主要关注降低偏差
  • bagging 子模型的训练可以并行进行，boosting 是串行模型，必须串行训练
  • bagging 模型的预测结果由各个子模型投票或加权平均得出，boosting 模型的预测结果由各个模型预测结果加起来
  • 哪些模型使用了 bagging
    • 随机森林

• 说出四个激活函数，以及优缺点

• XGBoost 过拟合怎么解决

• SVM 的细节，KKT 条件的意义

  • 在线性可分的约束条件下，最大化分类间隔
  • 利用拉格朗日乘数，将有约束最优化问题转为无约束最优化问题，由于是不等式约束，转化后是 min-max 优化问题
  • 对偶变换，min-max 问题转为 max-min 问题，SVM 中是强对偶关系，原问题和对偶问题解相同

• 求解关于 $\alpha$ 的二次规划问题

  • 利用 KKT 条件求 w, b
  • 得到分类决策函数

• MSE 为什么不能做分类损失

• 说说 softmax、交叉熵

$$softmax({\sigma }_i)=\frac{exp(x_i)}{{\sum }_{j=1}^{C}exp(x_j)},CrossEntropy=-\sum _{i=1}^C{y}_{i}log({\sigma }_i)$$

• 相对熵 / KL散度

$$KL(P||Q)=\sum P(x)log\frac{P(x)}{Q(x)}or\int P(x)log\frac{P(x)}{Q(x)}dx$$

• 互信息

$$I(X;Y)=\sum _{x\in X}\sum _{y\in Y}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$$

• 条件熵

$$H(X|Y)=-\sum _{x\in X}\sum _{y\in Y}p(x,y)logp(x|y)$$

• JS 散度

$$JS(P||Q)=\frac{1}{2}KL(P||\frac{P+Q}{2})+\frac{1}{2}KL(Q||\frac{P+Q}{2})$$

• 为什么使用 softmax？

  • 指数让大的更大，小的更小
  • 可微

• 生成式模型、判别式模型

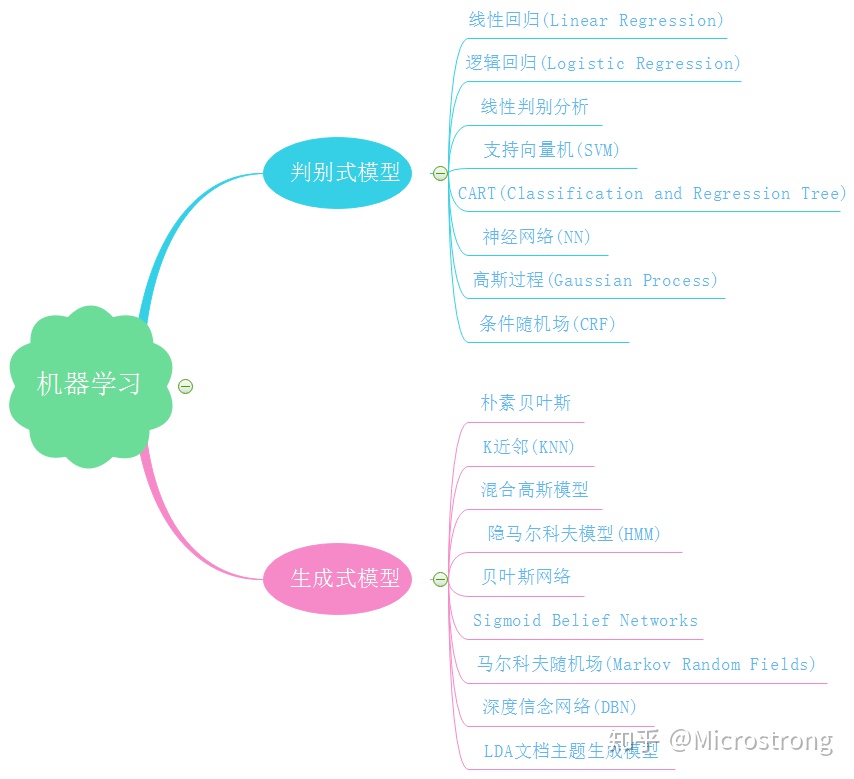
• 集成学习

  • 集成学习的核心是得到不一样且有一定准确率的基分类器，然后表决（从降低方差的角度）
  • boosting：有放回均匀采样
    • 主要关注降低偏差，所以应当尽量不让基学习器容量很大
  • stacking, boosting, bagging 随机森林
  • bagging，随机森林都是为了得到不同的基学习器
    • 随机森林：基学习器是决策树的 bagging + 属性扰动
  • 集成策略
    • 平均法
      • 简单平均
      • 加权平均（一般个体学习器性能差异较大时才采用）
    • 投票法
      • 绝对多数投票法
        • 某标记得票超过半数，则预测，否则拒绝预测
      • 相对多数投票法
        • 预测为得票最多的标记
      • 加权投票法
    • 学习法
      • stacking

• 熟悉DNN、CNN、RNN、LSTM等经典模型，对 Transformer、Attention 等熟悉者有加分

• 梯度消失、梯度爆炸

  出现原因：

  • 链式法则，梯度累乘效应导致梯度指数级增长或减小；梯度饱和（GAN，sigmoid，tanh）

  解决方案：

  • pre-training + fine-tunning
  • 梯度剪切：对梯度设定阈值，主要针对梯度爆炸
  • 权重正则化
  • 选择 relu 系的激活函数，梯度大部分是常数(1)
  • BN：把数据从饱和区拉到非饱和区
  • 残差网络系：resnet，densenet

• 神经网络基础知识

  • 权重共享、dropout
  • CNN 卷积计算尺寸
  • RNN
  • 你没有训练序列模型和强化学习模型的经历
    • 课题的时候花点时间
    • 强化学习 demo 跑一个

• 为什么分类问题损失函数不用 MSE 而用交叉熵

  • 由于使用 sigmoid (softmax)，MSE 求导的结果中包含 f(x)(1-f(x))，y=0，f(x)=1时，会有梯度消失问题；
  • MSE 是非凸的，有许多局部极小值点

• softmax 上溢下溢

  • 其实没有下溢，只有上溢（指数过大时：z = z - max(Z)）

• 交叉熵，极大似然估计, KL散度

• 常用损失函数

  • 指数损失：对异常点敏感

  • 对数似然

  • 交叉熵

  • 均方误差 (MSE)

    • 在模型输出与真实值的误差服从高斯分布的假设下，最小化均方差损失函数与极大似然估计本质上是一致的

  • 绝对误差 (MAE)

  • MSE 比 MAE 更快收敛，MAE 比 MSE 更 robust，更不易受异常点（outlier）影响

    • MAE 在 $|y_i-\widehat{y_i}|$ 很小时梯度同样为 1，不利于模型收敛

    • MAE 假设误差服从拉普拉斯分布，MSE 假设误差服从高斯分布，出现 outlier 拉普拉斯分布相比高斯分布受到的影响小得多

    • MSE 假设模型预测值和真实值之间的误差服从标准高斯分布 ($\mu =0,\sigma =1$)，则给定一个 $x_i$ ，模型输出真实值 $y_i$ 的概率为

    $$p(y_i|x_i)=\frac{1}{\sqrt{2\pi }}exp(-\frac{(y_i-\widehat{y_i}{)}^2}{2})$$

    进一步地，假设数据集中 N 个样本点之间相互独立，则给定所有 $x$ 输出所有真实值的概率，即似然 Likelihood，为所有 $p(y_i|x_i)$ 的累乘
    $$L(x,y)=\prod _{i=1}^N\frac{1}{\sqrt{2\pi }}exp(-\frac{(y_i-\widehat{y_i}{)}^2}{2})$$
    极小化负对数似然函数，并去掉无关项：
    $$\begin{gathered} NLL(x,y)=-log(L(x,y))=\frac{N}{2}log2\pi +\frac{1}{2}\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2 \\ NLL(x,y)=\frac{1}{2}\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2 \end{gathered}$$

• Huber Loss：$y_i$ 与 $\widehat{y_i}$ 差别大时 使用 MAE，降低 outlier 的影响；误差接近 0 时使用 MSE，使损失函数可到并且梯度更加稳定

• 激活函数优缺点

  • sigmoid，softmax，tanh，reLU，leakyReLU

• 梯度下降

  • 一阶梯度下降

    • 优化器

    • SGD，mini-batch,动量，RMSprop，adam

    • 学习率自动调整

      • 学习率衰减、预热、周期调整
      • AdaGrad：首先计算梯度平方的累加值，学习率逐渐衰减
      • $\Delta {\theta }_t=-\frac{\alpha }{\sqrt{G_t+ϵ}}\odot g_t$, $G_t={\sum }_{\tau =1}^t{g}_{\tau }\odot g_{\tau }$
      • RMSprop：把 AdaGrad 的梯度平方累积变为指数衰减移动平均

    • 梯度估计修正

      • 动量法：在第𝑡 次迭代时，计算负梯度的“加权移动平均”作为参数的更新方向
      • Adam：一方面计算梯度平方 g𝑡2 的指数加权平均（和 RMSprop 算法类似），另一方面计算梯度g𝑡 的指数加权平均（和动量法类似）

      Adam

      计算梯度平方 $g_t^2$ 的指数加权平均（RMSprop）：$G_t={\beta }_2{G}_{t-1}+(1-{\beta }_2)g_t\odot g_t$

      计算梯度梯度的指数加权平均（动量法）：$M_t={\beta }_1{M}_{t-1}+(1-{\beta }_1)g_t$

      假设 $M_0=0,G_0=0$，那么在迭代初期 $M_t$ 和 $G_t$ 得知会比真实的均值和方差要小，特别是当${\beta }_1,{\beta }_2$ 都接近 1 时，偏差会很大。因此，对偏差进行修正:
      $$\begin{gathered} \widehat{M_t}=\frac{M_t}{1-{\beta }_1^t} \\ \widehat{G_t}=\frac{G_t}{1-{\beta }_2^t} \end{gathered}$$
      参数更新：$\Delta {\theta }_t=-\frac{\alpha }{\sqrt{\widehat{G_t}+ϵ}}\widehat{M_t}$

      • 梯度截断（梯度爆炸）
  • 二阶梯度下降
    • 牛顿法
    • 拟牛顿法
    • BFGS…

• 分类评价标准

  准确率：左右样本被分类正确的比例。

  召回率：真实为正类的样本中，被判断为正类的占比。

  精准率：判断为正类的样本中，真实为正类的占比。

  f1分数：2召回率精准率/（召回率+精准率）

  假正率：负类中被分类为正类的占比。

  真正率：正类中被分类为正类的占比。(就是召回率)

  ROC、AUC等。

  ROC是指横坐标为假正率、纵坐标为真正率的曲线。真正率越高的同时，假正率低，就说明这个ROC曲线越好，曲线越陡。无视样本不平衡，因为无论正负样本比例如何变化，ROC都不会变。为了评估ROC的好坏，可能需要尝试不同的阈值（概率大于多少被判定为正类）。

  AUC（area under curve）是ROC曲线下的面积。

• 回归问题评价指标

  • MSE

  $$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

  • RMSE

  $$RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2}$$

  • MAE (平均绝对误差)

  $$MAE=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|$$

  • MAPE (平均百分比误差): 分母为 0 时不可用

  $$MAPE=\frac{100\%}{n}\sum _{i=1}^n\left|\frac{y_i-{\hat{y}}_i}{y_i}\right|$$

  • SMAPE (Symmetric Mean Absolute Percentage Error): 分母为 0 时不可用

  $$SMAPE=\frac{100\%}{n}\sum _{i=1}^n\frac{|y_i-{\hat{y}}_i|}{(|y_i|+|{\hat{y}}_i|)/2}$$

  • $R^2$

  $$R^2=1-\frac{SSE}{SST}=1-\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{{\sum }_{i=1}^n(y_i-{\bar{y}}_i{)}^2}$$

  • Adjusted R-square: 调整 R 方，n：数据点个数，k：特征个数

  $$Adjusted{R}^2=1-\frac{(1-R^2)(n-1)}{(n-k-1)}$$

• 多重共线性

  • 出现原因

  多重共线性就是指一个解释变量的变化引起另一个解释变量的变化。

  原本自变量应该是各自独立，根据回归分析结果，能得知哪些因素对因变量 Y 有显著影响。

  如果各个自变量 x 之间有很强的线性关系，就无法固定其他变量，也就找不到 x 和 y 之间的真实关系了。

  此外，多重共线性的原因还可能包括：

  1. 数据不足，某些情况下，收集更多数据可以解决共线性问题；
  2. 错误使用虚拟变量。比如，同时将男、女两个虚拟变量都放入模型，此时必定出现共线性，称为完全共线性
  • 共线性判别指标
  1. VIF

• FM、FFM、DeepFM

• 机器学习特征工程
  • 数据预处理
    • 无量纲化
      • 标准化
      • 区间缩放
      • 标准化和归一化
    • 定量特征二值化
    • 定性特征哑编码
    • 缺失值计算
      • 填充
        • 常量填充
        • 插值填充
        • 已有数据训练模型预测缺失值
        • XGBoost
      • 删除
    • 数据变换
  • 特征选择
    • Filter 过滤法
      • 方差选择法，选择方差大（设定阈值）的特征
      • 相关系数法，计算特征对目标值的相关系数和P值
      • 卡方检验
      • 互信息
    • Wapper 包装法
      • 通过消除特征获得不同特征集训练模型
    • Embedded 集成法（学习器自动选择特征）
      • 基于惩罚项
      • 基于树模型
    • 组合特征
      • FM
      • 决策树
      • 先验知识
  • 降维
    • 主成分分析
    • 线性判别分析
    • 自编码器

SVM

线性不可分的线性支持向量机（软间隔最大化）的学习问题变成如下凸二次规划问题（convex quadratic programming）问题（原始问题）
$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i \\ s.t.y_i(w\cdot x_i+b)\ge 1-{\xi }_i,i=1,2,...,N \\ {\xi }_i\ge 0,i=1,2,...,N \end{gathered}$$
上述原始最优化问题的拉格朗日函数是：
$$\begin{gathered} L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i[y_i(w\cdot x_i+b)-1+{\xi }_i]-\sum _{i=1}^N{\mu }_i{\xi }_i \\ 其中，{\alpha }_i\ge 0,{\mu }_i\ge 0 \end{gathered}$$
对偶问题是拉格朗日函数的极大极小问题。
$$\begin{gathered} \underset{\alpha ,\mu }{\max }\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu ) \\ s.t.{\alpha }_i\ge 0,{\mu }_i\ge 0,i=1,2,...,N \end{gathered}$$
首先求 $L(w,b,\xi ,\alpha ,\mu )$ 对 $w,b,\xi$ 的极小，由
$$\begin{gathered} {\nabla }_{w}L(w,b,\xi ,\alpha ,\mu )=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0 \\ {\nabla }_{b}L(w,b,\xi ,\alpha ,\mu )=-\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ {\nabla }_{{\xi }_i}L(w,b,\xi ,\alpha ,\mu )=C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
得
$$\begin{gathered} w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i \\ \sum _{i=1}^N{\alpha }_i{y}_i=0 \\ C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
代入拉格朗日函数得：
KaTeX parse error: No such environment: align at position 175: …pha_i \\ \begin{̲a̲l̲i̲g̲n̲}̲ s.t. \quad &\s…
将对偶最优化问题：利用等式约束 $C-{\alpha }_i-{\mu }_i=0$ 消去 ${\mu }_i$，并将约束写成：
$$0\le {\alpha }_i\le C$$
将极大问题转化为极小问题，得到：
KaTeX parse error: No such environment: align at position 119: …pha_i \\ \begin{̲a̲l̲i̲g̲n̲}̲ s.t. \quad &\s…
定理 7.3 设 ${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$ 是对偶问题的解，若存在 ${\alpha }^{\ast }$ 的一个分量 ${\alpha }_j^{\ast }$ ，满足 $0<{\alpha }_j^{\ast }<C$，则原始问题的解 $w^{\ast },b^{\ast }$ 可按下式求得：
$$\begin{gathered} w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i \\ {b}^{\ast }=y_j-\sum _{i=1}^N{y}_i{\alpha }_i^{\ast }(x_i\cdot x_j) \end{gathered}$$
证明： 原始问题是凸二次规划问题，解满足 KKT 条件，即
$$\begin{gathered} {\nabla }_{w}L(w^{\ast },b^{\ast },{\xi }^{\ast },{\alpha }^{\ast },{\mu }^{\ast })=w^{\ast }-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i=0 \\ {\nabla }_{b}L(w^{\ast },b^{\ast },{\xi }^{\ast },{\alpha }^{\ast },{\mu }^{\ast })=-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i=0 \\ {\nabla }_{{\xi }_i}L(w^{\ast },b^{\ast },{\xi }^{\ast },{\alpha }^{\ast },{\mu }^{\ast })=C-{\alpha }_i^{\ast }-{\mu }_i^{\ast }=0 \\ {\alpha }_i^{\ast }[y_i(w^{\ast }\cdot x_i+b^{\ast })-1+{\xi }_i^{\ast }]=0 \\ {\mu }_i^{\ast }{\xi }_i^{\ast }=0 \\ {y}_i(w^{\ast }\cdot x_i+b^{\ast })-1+{\xi }_i^{\ast }\ge 0 \\ {\xi }_i^{\ast }\ge 0 \\ {\alpha }_i^{\ast }\ge 0 \\ {\mu }_i^{\ast }\ge 0,i=1,2,...,N \end{gathered}$$
若存在 ${\alpha }_j^{\ast }$ ，满足 $0<{\alpha }_j^{\ast }<C$，则 $y_i(w^{\ast }\cdot x_i+b^{\ast })-1=0$，得证。

分类超平面可写成
$$\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x\cdot x_i)+b^{\ast }=0$$
分类决策函数可以写成
$$f(x)=sign\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x\cdot x_i)+b^{\ast }\right)$$
求解过程不写，基本就是解凸二次规划得到 ${\alpha }^{\ast }$ 利用 KKT 条件算 $w^{\ast },b^{\ast }$，从而得到分类超平面及分类决策函数。

拉格朗日对偶性

1. 原始问题

   假设$f(x),c_i(x),h_j(x)$是定义在$R^n$上的连续可微函数，考虑约束最优化问题

$$\begin{gathered} \underset{x\in R^n}{\min }f(x) \\ s.t.c_i(x)\le 0,i=1,2,...,k \\ {h}_j(x)=0,j=1,2,...,l \end{gathered}$$

称此约束最优化问题为原始最优化问题或原始问题。

​ 引进广义拉格朗日函数
$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)$$
这里，${\alpha }_i\ge 0,{\beta }_j$ 是拉格朗日乘子，考虑 $x$ 的函数：
$${\theta }_P(x)=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
P 表示原始问题。

​ 假设给定某个 $x$ 如果违反原始问题的约束条件，即存在某个 i 使得 $c_i(x)>0$ 或者存在某个 j 使得 $h_j(x)$，那么就有
$${\theta }_P(x)=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\left[f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)\right]=+\infty$$
因为若某个 i 使得 $c_i(x)>0$，则可令 ${\alpha }_i\to +\infty$，若某个 j 使得 $h_j(x)\ne 0$，则可令 ${\beta }_j{h}_j(x)\to +\infty$，而将其余 $\alpha ,\beta$ 取 0.

​ 相反地，如果 $x$ 满足约束条件时，有约束条件可知 ${\theta }_P(x)=f(x)$ 。因此，
$${\theta }_P(x)=\{\begin{array}{rlr}f(x),& & x满足原始问题约束\\ +\infty ,& & 其他\end{array}$$
所以考虑极小化问题
$$\underset{x}{\min }{\theta }_P(x)=\underset{x}{\min }\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
它与原始优化问题有相同的解，被称为广义拉格朗日函数的极大极小问题。定义原始问题的最优值
$$p^{\ast }=\underset{x}{\min }{\theta }_P(x)$$

2. 对偶问题

   定义：

$${\theta }_D(\alpha ,\beta )=\underset{x}{\min }L(x,\alpha ,\beta )$$

再考虑极大化 ${\theta }_D(\alpha ,\beta )$ ，即
$$\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }{\theta }_D(\alpha ,\beta )=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )$$
上述问题称为广义拉格朗日函数的极大极小问题，可以将广义拉格朗日函数的极大极小问题表示为约束优化问题：
$$\begin{gathered} \underset{\alpha ,\beta }{\max }{\theta }_D(\alpha ,\beta )=\underset{\alpha ,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta ) \\ s.t.{\alpha }_i\ge 0,i=1,2,...,k \end{gathered}$$
上述问题称为原始问题的对偶问题，定义对偶问题的最优值：
$$d^{\ast }=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }{\theta }_D(\alpha ,\beta )$$

3. 原始问题和对偶问题的关系

   定理 1 若原始问题和对偶问题都有最优值，则

$$d^{\ast }=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )\le \underset{x}{\min }\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )=p^{\ast }$$
证明：对任意的 $\alpha ,\beta ,x$ 有
$${\theta }_D(\alpha ,\beta )=\underset{x}{\min }L(x,\alpha ,\beta )\le L(x,\alpha ,\beta )\le \underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )\le {\theta }_P(x)$$
即：${\theta }_D(\alpha ,\beta )\le {\theta }_P(x)$，由于原始问题和对偶问题均有解，所以
$$\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }{\theta }_D(\alpha ,\beta )\le \underset{x}{\min }{\theta }_P(x)$$
即：
$$d^{\ast }=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )\le \underset{x}{\min }\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )=p^{\ast }$$
**推论 1 **设 $x^{\ast }$ 和 ${\alpha }^{\ast },{\beta }^{\ast }$ 分别是原始问题和对偶问题的解，并且 $d^{\ast }=p^{\ast }$ 。则 $x^{\ast }$ 和 ${\alpha }^{\ast },{\beta }^{\ast }$ 分别是原始问题和对偶问题的最优解。

​ 在某些条件下，原始问题和对偶问题的最优值相等，这时可以用解对偶问题替代解原始问题。下面以定理的形式叙述有关的重要结论而不予证明。

定理 2 考虑原始问题和对偶问题，假设

1. 函数 $f(x)$ 和 $c_i(x)$ 是凸函数；
2. $h_j(x)$ 是仿射函数；
3. 不等式约束是严格可行的，即存在 $x$，对所有 $i$，有 $c_i(x)<0$；

则存在 $x^{\ast },{\alpha }^{\ast },{\beta }^{\ast }$ ，使 $x^{\ast }$ 是原始问题的解，${\alpha }^{\ast },{\beta }^{\ast }$ 是对偶问题的解，并且
$$d^{\ast }=p^{\ast }=L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })$$
定理 3 若原始问题和对偶问题满足 定理 2 的条件，则 $x^{\ast }$ 和 ${\alpha }^{\ast },{\beta }^{\ast }$ 分别是原始问题和对偶问题的解的充分必要条件是 $x^{\ast },{\alpha }^{\ast },{\beta }^{\ast }$ 满足下列 Karush-Kuhn-Tucker (KKT) 条件：
$$\begin{gathered} {\nabla }_{x}L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \\ {\alpha }_i^{\ast }{c}_i(x^{\ast })=0,i=1,2,...,k \\ {c}_i(x^{\ast })\le 0,i=1,2,...,k \\ {\alpha }_i^{\ast }\ge 0,i=1,2,...,k \\ {h}_j(x^{\ast })=0,j=1,2,...,l \end{gathered}$$
上面第二个条件称为 KKT 的对偶互补条件（此条件的意思是，若 $x^{\ast },{\alpha }^{\ast },{\beta }^{\ast }$ 是最优解，则原始问题中的拉格朗日余项等于 0.）。由此条件可知：若 ${\alpha }_i^{\ast }>0$，则 $c_i(x^{\ast })=0$.

SVM：逐句话、逐个公式的推导

LR 原理推导，损失函数，求解方法

决策树细节

编程题：

不熟悉的：

• 股票买卖
• 链表、二叉树的指针操作，哨兵，边界条件处理
• 优先队列
• 单调栈
• 堆排序
• 字符串理解
• 二分法（旋转数组），边界条件
• 单例模式
• 多线程
• 子序列和子串

面试遇到的：

• 字节：字符串编辑距离
• 百度：最长公共子序列
• 茄子：有序数组生成二叉平衡搜索树
• 寒武纪：排序怎么多核心并行，卷积感受野计算公式，计算一组数的全排列
• 华为：后序遍历中序遍历构造二叉树，搬货物
• 小米：层序遍历二叉树，链表翻转