机械滞后角

机械滞后角：振动响应滞后于不平衡力的角度

给转子一个激振力 f = F*sin(wt)，则响应为 x = A*sin(wt-φ)

My'' + Cy' + Ky = F*sin(wt)
y'' + 2*ξwn + wn^2*y = F/M*sin(wt)
解 y=A*sin(wt-φ)
其中

 

下图即为位移的相位滞后于激励力

atan的曲线

φ=0？
由atan曲线可看出，自变量为0则因变量为0，也就是分子ξ*wn*w=0
w为激励频率，wn=sqrt(K/M)，w与wn都不可能为0
只有阻尼比ξ=0，则滞后角为0
也就是说滞后角是由于阻尼产生的。至于阻尼属于什么类型，我还有待学习。

随w变化时，φ如何变？
ξ=C/(2*m*wn)  ， (2*m*wn) 为临界阻尼
令 φ=atan(ψ)，即我将里面的一堆用ψ表示
w>wn 则ψ<0，，φ位于-90°~0°
w<wn 则ψ>0，φ位于0°~90°
w=wn 则ψ=＋∞，φ趋于90°，此时阻尼与滞后角无关，滞后角就是固定的一个数，即90°

设m=C，wn=1

下图是 φ<0时，φ=φ+pi，即将后半段翻折上去，书上都是如下图表示，但我不理解为什么要翻折。

动平衡时，配平位置需要由振动高点反向转滞后角
下图，3表示键相点、2表示振动高点、1表示不平衡力位置。在实际转子上只有3点
那么如何确定2点与1点？
键相信号与振动信号确定出一个相位角φ1，则由3点逆时针转φ1到2点，2点即振动高点
从2点顺时针转滞后角φ2到1点，1点即不平衡力位置，需要在1点的对面加配重

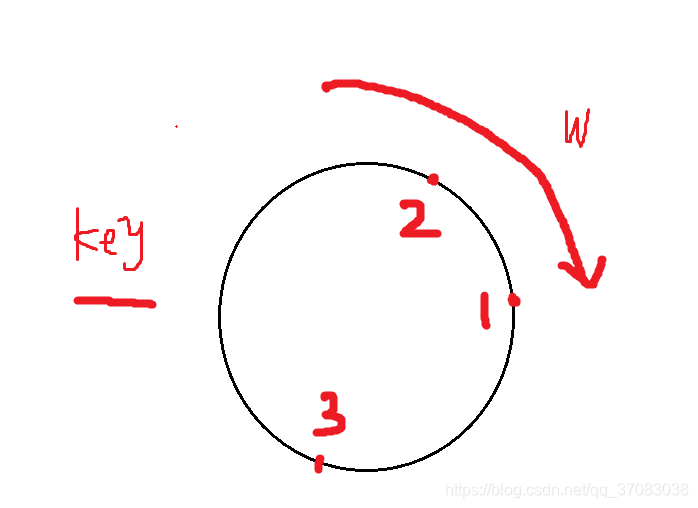
φ1可以从信号中计算出来，那么φ2怎么确定呢？
方1——大致在一个范围内取值
如果转速低于临界转速，φ2在0°~90°之间取一个数
如果转速高于临界转速，φ2在90°~180°之间取一个数
如果转速在临界转速附近，φ2取90°

方2——影响系数法
原始振动，A11，φ11
在键相点逆时针转φ3处加试重m 单位g，A12，φ12
(φ11表示测得第一个φ1，φ12表示测得第二个φ1)
[(A12,φ12）- (A11,φ11)]/(m,φ3) = (n,φ4) ， α = (n,φ4) 为影响系数
- (A11,φ11)/α = (p,φ5)  即应在键相点逆时针转φ5处，加配重p 单位g
用影响系数法则避开了滞后角的确定

用复指数表示
原始振动，A11*exp(i*φ11)
在键相点逆时针转φ3处加试重m 单位g，A12*exp(i*φ12)
(φ11表示测得第一个φ1，φ12表示测得第二个φ1)
[A11*exp(i*φ11) - A12*exp(i*φ12)]/m*exp(i*φ3) = n*exp(i*φ4)
- A11*exp(i*φ11)/n*exp(i*φ4) = p*exp(i*φ5)
即应在键相点逆时针转φ5处，加配重p 单位g

附段代码说明A*exp(i*φ)与(A,φ)如何转化

a = 5
b = 90/360*2*np.pi
c = a*np.exp(1j*b)
c_real = np.real(c)
c_imag = np.imag(c)
a_ = np.sqrt(c_imag**2 + c_real**2)
b_ = np.arctan(c_imag/c_real)
print(a,b,a_,b_)

影响系数法用图表示，我用两种方式表示
两个圆分别是加试重前后的振幅A11 A12为半径绘制的

用轴颈半径绘制的圆

第二张图的说明：
键相点3
由键相点逆时针转φ11找到原始不平衡的振动高点11，高点11顺时针转滞后角φ2到原始不平衡力的位置21
在轴上点4处加试重
由键相点逆时针转φ12找到加试重后的振动高点12，，高点12顺时针转滞后角φ2到加试重后不平衡力的位置22
即用两个振动高点就避开了滞后角的确定，我根本不需要确定滞后角φ2的大小(不用确定不平衡力的位置)，只要知道两个振动高点的位置即可。