量纲分析

举例

美国原子弹爆炸图

Taylor利用量纲分析法，计算出爆炸形成的冲击波半径R与时间有关

释放的能量E、冲击波半径R、空气密度ρ、空气绝热系数γ（无量纲数）、时间t，，用量纲分析求出未知指数，x1=1/5，x2=-1/5，x3=2/5。

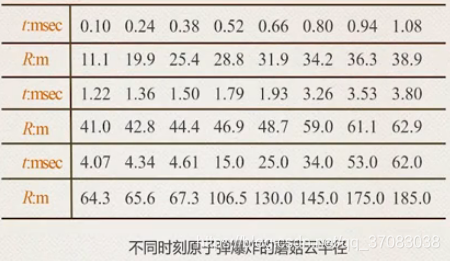
根据某次原子弹爆炸的照片数据，计算出原子弹的能量。
泰勒得出在一些小型爆炸中。
密度取1.25 kg/m^3
训练数据R,t已知
则根据公式，可以计算出E

Von Neumann 冯诺依曼

基本量纲与导出量纲

F 单位 N 基本量纲 M*L/T^2
m 单位 kg 基本量纲 M
a 单位 m/s^2 基本量纲 L/T^2

无量纲量与无量纲单位

无量纲量是个没有单位的数字，量纲为1。与1，前者纲量为，后者量纲为1

无量纲量：圆周率Pi、欧拉常数e、分贝dB、弧度、应变、宾汉数、摩擦系数、欧拉数、马赫数、雷诺数、品质因子等。

无量纲单位：摩尔分数（mol/mol）、质量百分浓度（kg/kg）、度（°）、弧度（rad）等。

量纲分析

针对某一问题，如果已知R与的模型，需要确定未知参数，可通过量纲分析来确定

举个例子：
已知。，可确定出a,b,c...。

难点：
1、确定哪些物理量有关，如确定R与u、v有关
2、确定模型，如确定R=u^a * v^b

白金汉Pi定理

白金汉Pi定理：设影响某现象的物理量数为n个，这些物理量的基本量纲为m个，则该物理现象可用n-m个独立的无量纲数群（准数）关系式表示
量纲法则：1.只有量纲相同的物理量，才能彼此相加、相减和相等； 2.指数函数、对数函数和三角函数的宗量应当是量纲1。

论文 浅谈量纲法则的合理应用

重写方程

确定常数a1~an，b1~bn，....，可将方程重写

疑问

解析 一词怎么解释？