代数方程与差分方程模型（二）：原子弹爆炸的能量估计

基本想法

冲击波的爆炸由“蘑菇云”反映出来，“蘑菇云”越大，扩散速度越快，能量越大。

假设：爆炸产生的冲击波以爆炸点为中心呈球面向四周传播，爆炸的能量越大，在一定时刻冲击波传播的越远。

泰勒测量：时刻t所对应的“蘑菇云” 的半径r
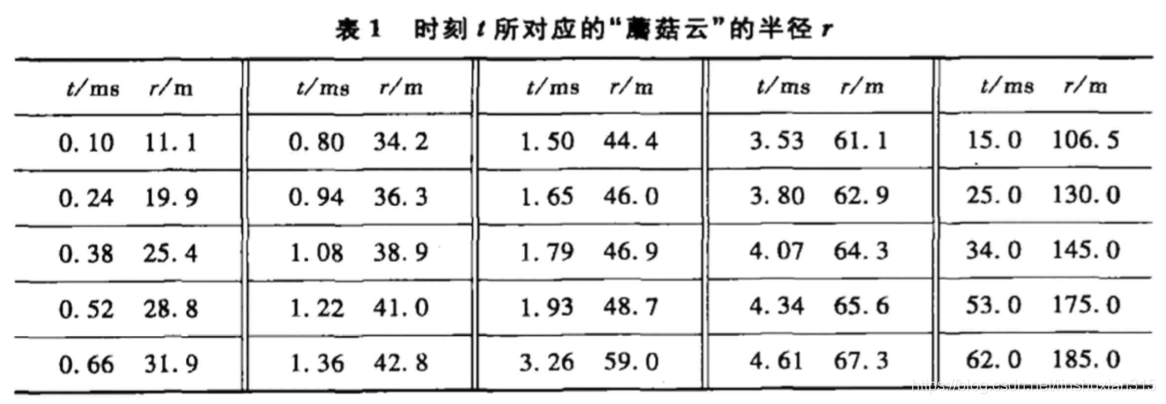泰勒用量纲分析法建立数学模型，辅以小型试验，又利用测量数据对爆炸的能量进行估计。

量纲分析法

量纲齐次原则

动力学中基本量纲	导出量纲
长度l的量纲L[l]	速度v的量纲[v]=LT-1
质量m的量纲M[m]	加速度a的量纲[a]=LT-2
时间t的量纲T[t]	力f的量纲[f]=LMT-2

引力常数k的量纲[k] ($f=k\frac{m_1{m}_2}{r^2}$)
$[k]=[f][l{]}^2[m{]}^{-2}=L^3{M}^{-1}{T}^{-2}$
对无量纲量 α，α=1(=L⁰M⁰T⁰)

eg.单摆运动

求摆动周期的表达式
设物理量t，m，l，g之间有关系式，$t=\lambda m^{{\alpha }_1}{l}^{{\alpha }_2}{g}^{a_3}(1)$
${\alpha }_1,{\alpha }_2,{\alpha }_3为待定系数，\lambda 为无量纲量$
$(1)的量纲表达式[t]=[m{]}^{{\alpha }_1}[l{]}^{{\alpha }_2}[g{]}^{{\alpha }_3}$
推导出$T=M^{{\alpha }_1}{L}^{{\alpha }_2+{\alpha }_3}{T}^{-2{\alpha }_3}$

Pi定理

$设f(q_1,q_2,...,q_m)=0$
$是与量纲单位无关的物理定律，X_1,X_2,...X_n是基本量纲，n\le m，q_1,q_2,...q_m的量纲可表为[q_j]={\prod }_{i=1}^n{X}_i^{a_{ij}},j=1,2,...,m$
量 纲 矩 阵 记 作 A = { a i j } n × m , 若 r a n k A = r 量纲矩阵记作A=\{a_{ij}\}_{n×m},若rankA=r 量纲矩阵记作A={aij​}n×m​,若rankA=r
$线性齐次方程组有Ay=0有m-r个基本解，$
$记作y_s=(y_{s1},y_{s2},...,y_{sm}{)}^T,s=1,2,...,m-r$
$则{\pi }_s={\prod }_{j=1}^m{q}_j^{y_j(s)}为m-r个无量纲的量，且$
$F({\pi }_1,{\pi }_2,...,{\pi }_{m-r})=0与f(q_1,q_2,...,q_m)=0等价，F未定$

原子弹爆炸能量估计的量纲分析方法建模

记爆炸能量为E，将“蘑菇云”近似看成一个球形，
时刻t球的半径为r
思考：r与哪些因素有关？
回答：t，E，空气密度ρ，大气压强P
得出$r=\phi (t,E,\rho ,P)$
进而有$f(r,t,E,\rho ,P)=0$
基本量纲:$L,M,T$
量纲矩阵是

$RankA=3导出Ay=0，y=(y_1,y_2,y_3,y_4,y_5{)}^T有2个基本解$

即得出
由于时间t非常短，能量非常大
借助小型爆炸数据确定λ≈1

空气密度ρ=1.25(kg/m³),用r，t的实际数据取平均，得出E=8.2825×10¹³(焦耳)。因为1千吨TNT炸药的能量是4.184×10¹²焦耳，可得爆炸的能量为E=19.7957(千吨)。

泰勒的计算(取对数)

$r=(\frac{t^{2}E}{\rho }{)}^{\frac{1}{5}}\to lo{g}_{10}r=\frac{2}{5}lo{g}_{10}t+\frac{1}{2}lo{g}_{10}(\frac{E}{\rho })\to 令y=c=\frac{1}{2}lo{g}_{10}(\frac{E}{\rho })\to y=\frac{5}{2}lo{g}_{10}r-lo{g}_{10}(t)$
$取y平均值得c=6.9038$
$因此E=8.0276\times 10^{13}(焦耳)即19.2吨$

最小二乘法拟合r=at^b

b=0.4058与2/5非常接近