精读论文：Sparse Coding with Variance Regularization

Sparse Coding with Variance Regularization

\quad
本文的主题是 sparse coding。这个主题在computer vision中非常常见，因为我们需要提取出图像的 representation，而且尽可能要求是稀疏表示。通常的 sparse coding算法是用 ${\ell }_1$ 的惩罚函数（penalty function）来限制字典的稀疏性。在这篇文章中，作者提出了一种全新的框架，在这个框架中我们不再需要对 decoder 使用某种正则函数。
\quad

Abstract

在文中首先提出了一个问题：“ Collapse of the ${\ell }_1$ norm in the codes”。也就是说${\ell }_1$范数崩溃的问题。为什么会造成这个问题呢？首先，现有一个字典为$\mathcal{D}$，重构信号为$\hat{y}$，那么有
$$y=\mathcal{D}z=c\mathcal{D}\cdot \frac{1}{c}z$$
成立，这个意思就是说，当$c>1$时，$\frac{1}{c}z$比原来的$z$会更小，但其实这会有一模一样的重构。此时，如果不对$\mathcal{D}$做限制，$\mathcal{D}$无限大，就会导致$z$无限小，这就是${\ell }_1$范数崩溃问题。

传统的方法是利用二范数去规范化字典，但是文中指出这样的规范化是不平凡的，所以本文提出了方差正则化方法，直接对$z$进行约束，省去了对字典进行约束的步骤。（这里的方差正则化是直接加在损失函数上的）

同时，文中的方差正则化其实就是“Let each latent code component has variance greater than a fixed threshold”。后文会对这里进行详细解释。

另外，文中实验表明，使用了非线性Deocder的带方差正则化的AutoEncoder框架相比于线性decoder的框架具有更高的重构质量。同时，使用了方差正则化的稀疏表示方法在降噪和分类任务也具有很好的效果。
\quad

Sparse AutoEncoder Framework

下图是文中提出的AutoEncoder框架，这个框架其实是比较漂亮的。

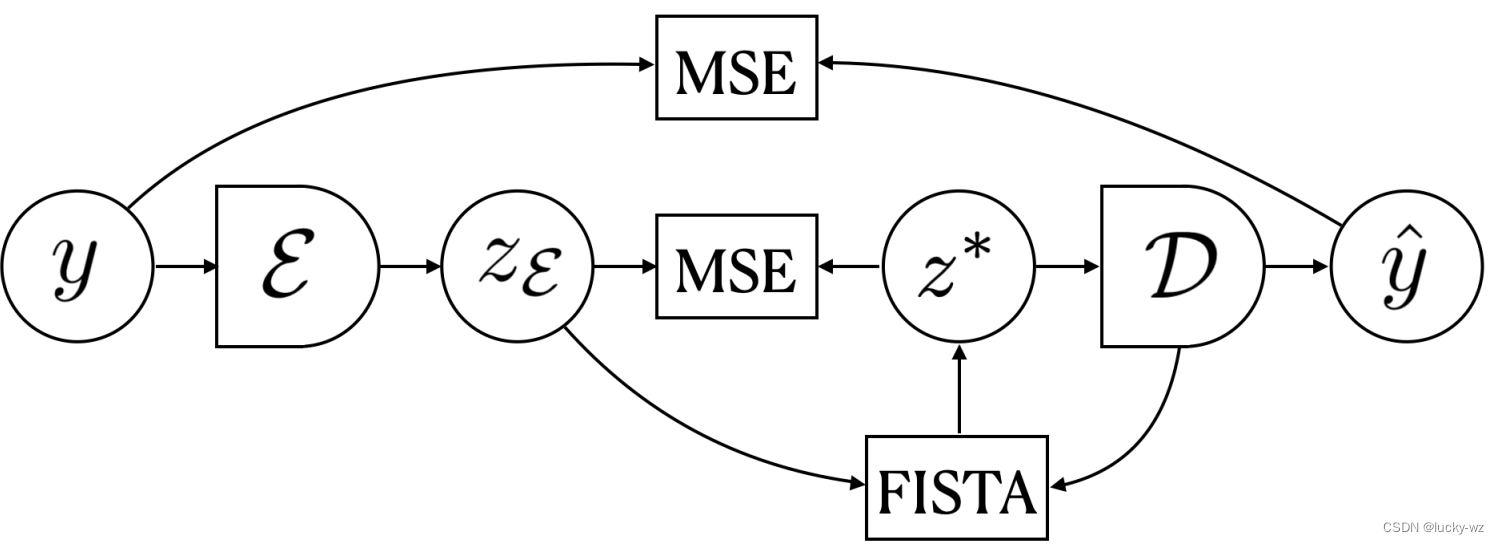
给定一个输入$y$（图片）和一个固定的decoder $\mathcal{D}$，使用FISTA找到一个sparse code $z^{\ast }$可以使用字典$\mathcal{D}$的元素重构$y$。

整个框架的输入为图片$y$。

• 首先，将图片$y$输入到Encoder里面，得到输出$z_{\epsilon }$；
• 其次，将$z_{\epsilon }$和$\mathcal{D}$输入到FISTA中，经过若干步迭代，可以得到$z^{\ast }$。这里的迭代有一个损失函数，可以更新对应的参数。（其实这里的FISTA更像是LISTA）这里的损失函数一共分为三部分：
  • 方差正则化
  • $MSE(z_{\epsilon },z^{\ast })$
  • $MSE(y,\hat{y})$
• 将$z^{\ast }$传入Decoder中，重构信号$y$。

注意：在FISTA中，输入$z_{\epsilon }$其实是作为FISTA迭代的初值，可以减少迭代次数，加快FISTA的收敛。另外，传入$\mathcal{D}$（参数固定）是为了重构信号$y$。这就是说，这里想要FISTA得到的$z^{\ast }$同时满足两个条件：（1）和Encoder得到的$z_{\epsilon }$足够接近；（2）要求能较好的重构信号$y$。

接下来详细讲一讲每部分的细节。

\quad

Background: Sparse Coding and Dictionary Learning

首先来看一下背景知识，知道的略过。

稀疏编码算法就是在给定一个固定的字典$\mathcal{D}\in {\mathbb{R}}^{d\times l}$和样本$y\in {\mathbb{R}}^d$的基础上，寻求一个潜在的稀疏表示的算法。一般通过最小化能量函数求解：
$$z^{\ast }=\arg \underset{z}{\min }\mathbf{E}(z,y,\mathcal{D})=\frac{1}{2}\Vert y-\mathcal{D}z{\Vert }_2^2+\lambda \Vert z{\Vert }_1$$

其实一般情况下字典也是不知道的，字典$\mathcal{D}$的参数一般利用梯度下降算法最小化均方误差求解得到：
$${\mathcal{L}}_{\mathcal{D}}\left(\mathcal{D},{\mathcal{Z}}^{\ast },\mathcal{Y}\right)=\arg \underset{\mathcal{D}}{\min }\frac{1}{N}\sum _{i=1}^N{\Vert y_i-\mathcal{D}{z}_i^{\ast }\Vert }_2^2$$
方便起见，(1)式重新写为：
$$z^{\ast }=\arg \underset{z}{\min }\mathbf{E}(z,y,\mathcal{D})=\arg \underset{z}{\min }f(z)+g(z)$$

这里先讲一讲ISTA算法 ，一个ISTA迭代可以分为两步：Gradient Step 和 Shrinkage Step。

• Gradient Step

$${\tilde{z}}^{(k)}=z^{(k-1)}-{\eta }_k\nabla f\left(z^{(k-1)}\right)$$

• Shrinkage Step

$$z^{(k)}={\tau }_{\lambda {\eta }_k}\left({\tilde{z}}^{(k)}\right)$$
其中，${\tau }_{\alpha }(x{)}_j=\mathrm{sign}\left(x_j\right){\left(\left|x_j\right|-\alpha \right)}_{+}$。ISTA详细步骤可以看之前写的文章：Iterative Shrinkage Thresholding Algorithm

FISTA比较简单，它其实就是在ISTA的基础上加了一个动量项，进行了加速。Gradient Step式中的$z^{k-1}$被替换为：
$$x^{(k)}=z^{(k-1)}+\frac{t_{k-1}-1}{t_k}\left(z^{(k-1)}-z^{(k-2)}\right)$$
令$t_1=1$，对于$k\ge 2$有：
$$t_k=\frac{1+\sqrt{1+4t_{k-1}^2}}{2}$$
因此，FISTA的 Gradient Step变为了：
$${\tilde{z}}^{(k)}=x^{(k)}-{\eta }_k\nabla f\left(x^{(k)}\right)$$
Shrinkage Step和ISTA一样。

\quad

(F)ISTA with Variance Regularization

为了防止${\ell }_1$范数的崩溃，在原来的优化问题上加入方差正则化：
$$\tilde{f}(\mathbf{z})=\underset{\text{reconstruction terms}}{\underbrace{\sum _{i=1}^n\frac{1}{2}{\Vert y_i-\mathcal{D}{\mathbf{z}}_{\cdot i}\Vert }_2^2}}+\underset{\text{squared hinge terms}}{\underbrace{\sum _{j=1}^l\beta {\left[{\left(T-\sqrt{\mathrm{Var}\left({\mathbf{z}}_{j\cdot }\right)}\right)}_{+}\right]}^2}}$$
其中，$\mathrm{Var}\left({\mathbf{z}}_{j.}\right)=\frac{1}{n-1}\sum _{i=1}^n{\left({\mathbf{z}}_{ji}-{\mu }_j\right)}^2$。

在此基础上，加入${\ell }_1$正则化项，可以得到修正后的能量函数：
$$\tilde{\mathbf{E}}(\mathbf{z},Y,\mathcal{D})=\sum _{i=1}^n\frac{1}{2}{\Vert y_i-\mathcal{D}{\mathbf{z}}_{\cdot i}\Vert }_2^2+\sum _{j=1}^l\beta {\left[{\left(T-\sqrt{\mathrm{Var}\left({\mathbf{z}}_{j\cdot }\right)}\right)}_{+}\right]}^2+\sum _{i=1}^n\lambda {\Vert {\mathbf{z}}_{\cdot i}\Vert }_1$$

不知道大家对这个方差正则化是否理解，我来谈谈自己的一点想法：关注hinge term这一项，我们最小化$\tilde{\mathbf{E}}(\mathbf{z},Y,\mathcal{D})$时，由于平方的存在，理想情况下是想hinge term这一项越小越好，里面的$\left(T-\sqrt{\mathrm{Var}\left({\mathbf{z}}_{j\cdot }\right)}\right)$这部分本身就非负（简单的理解，其实$({)}_{+}$就是ReLU），所以这部分越小越小，其实就是让$z$的方差大于一个固定的阈值$\sqrt{T}$。

与上面的ISTA类似，分别讨论 Gradient Step 和 Shrinkage Step：

• Gradient Step：
  $${\tilde{\mathbf{z}}}_{\cdot t}^{(k)}={\mathbf{z}}_{\cdot t}^{(k-1)}-{\eta }_k{\nabla }_{{\mathbf{z}}_{\cdot t}^{(k-1)}}\tilde{f}(\mathbf{z})$$

  • reconstruction terms
    $$\frac{\partial }{\partial {\mathbf{z}}_{st}}\sum _{i=1}^n\frac{1}{2}{\Vert y_i-\mathcal{D}{\mathbf{z}}_{\cdot }\Vert }_2^2={\mathcal{D}}_s^T\left(\mathcal{D}{\mathbf{z}}_{\cdot t}-y_t\right)$$
  • hinge terms
    $$\frac{\partial }{\partial {\mathbf{z}}_{st}}\sum _{j=1}^l\beta {\left[{\left(T-\sqrt{\mathrm{Var}\left({\mathbf{z}}_{j.}\right)}\right)}_{+}\right]}^2=\{\begin{array}{ll}-\frac{2\beta }{n-1}\frac{T-\sqrt{\mathrm{Var}\left({\mathbf{z}}_{s.}\right)}}{\sqrt{\mathrm{Var}({\mathbf{z}}_{s.)}}}\left({\mathbf{z}}_{st}-{\mu }_s\right),& \text{ if }\sqrt{\mathrm{Var}\left({\mathbf{z}}_{s.}\right)}<T\\ 0& \text{ otherwise }\end{array}$$

• Shrinkage Step：与ISTA一样。

AutoEncoder Architectures

Encoder

Encoder的架构如下：

这里的Encoder的架构采用的2010年发表的LISTA的架构。要注意的是，Encoder的输出层也作用了ReLU，也就是说，Encoder的输出是非负的，同时也是较为稀疏。
\quad

Decoder

Decoder其实就相当于字典的存在，也就是说：
$y=\mathcal{D}x$
可以$\mathcal{D}$看作一个映射，把 $z^{\ast }\to \hat{y}$。自然地，这个映射有线性的，也有非线性的。在论文中，作者使用了两种Decoder，分别为：

• Linear Decoder: A simple linear transformation $W\in {\mathbb{R}}^{d\times l}$.
• Non-Linear Decoder: Networks with one hidden layer. (parameters: $W_1\in {\mathbb{R}}^{m\times l}$, $b_1\in {\mathbb{R}}^m$, $W_2\in {\mathbb{R}}^{d\times m}$)

并且，论文中的实验说明了非线性的Decoder的效果比线性的Decoder效果更好。

\quad

Training

一些训练的细节：

• 利用Encoder得到的结果当作FISTA的初值，减少迭代次数；
• 限制$z$为非负，简化Shrinkage为ReLU；
• $\lambda$的值取决于稀疏程度；
• 四组算法：SDL、SDL-NL、VDL、VDL-NL
  • SDL：standard dictionary learning.
  • SDL-NL： SDL with non-linear decoder.
  • VDL：variance-regularized dictionary learning.
  • VDL-NL：VDL with non-linear decoder.
• 数据集：MNIST VS Natural Image Patches.
• 评估： PSNR

提到PSNR，这里简单说一下PSNR的计算公式。给定一个大小为$m\times n$的干净图像$I$和噪声图像$K$，均方误差($MSE$)定义为：
$$MSE=\frac{1}{mn}\sum _{i=0}^{m-1}\sum _{j=0}^{n-1}[I(i,j)-K(i,j){]}^2$$
在此基础上，PSNR(dB)被定义为：
$$PSNR=10\cdot {\log }_{10}\left(\frac{MA{X}_I^2}{MSE}\right)$$

其中$MA{X}_I^2$为图片可能的最大像素值。如果每个像素都由 8 位二进制来表示，那么就为 255。通常，如果像素值由$B$位二进制来表示，那么$MA{X}_I=2^B-1$。一般地，针对 uint8 数据，最大像素值为 255；针对浮点型数据，最大像素值为 1。

峰值信噪比PSNR衡量图像失真或是噪声水平的客观标准。

2个图像之间PSNR值越大，则越相似。普遍基准为30dB，30dB以下的图像劣化较为明显。

\quad

参考

• Evtimova K, LeCun Y. Sparse Coding with Multi-Layer Decoders using Variance Regularization[J]. arXiv preprint arXiv:2112.09214, 2021.