坐标转换+程序

最新推荐文章于 2024-05-08 16:10:40 发布

明码

最新推荐文章于 2024-05-08 16:10:40 发布

阅读量1.4k

点赞数 1

分类专栏： Motion Planning 文章标签：自动驾驶 python

本文链接：https://blog.csdn.net/qq_37087723/article/details/119531114

版权

Motion Planning 专栏收录该内容

18 篇文章 47 订阅

订阅专栏

2D世界与小车坐标系示例¶

为什么我们要获取目标在不同的坐标系下的位姿呢？我们通过以下的简单案例进行讲解并计算。

假如在一个世界坐标系下有一个小车和一个人，则很容易看出来他们两个在世界坐标系下的位置。
在这里插入图片描述
但事实上，我们通常能通过小车的摄像头或雷达等传感器，获取到人在小车坐标系 $O_r$
(下图的蓝色坐标系)下的位置 (5.5,4) ，那么如果我们只知道人在小车坐标系下的位置以及小车在世界坐标系下的位置，是否能够算出人在世界坐标系下的位置呢？
在这里插入图片描述那么，我们将两个坐标系进行合并，如果已知小车在世界坐标系下的位姿，并且小车可以通过传感器获取目标在小车坐标系下的 $O_r$ 的位姿,我们就可以算出来人在世界坐标系 $O_w$ 的位姿。

当然，就如同刚刚讲过的坐标系变换场景问题，坐标变换除了纯粹的平移关系，还会有纯粹的旋转关系，以及最常见两者的结合（平移+旋转）。接下来我们的目标就是求出在不同的坐标系变换关系下，目标的位姿以及其变换关系。

平移变换

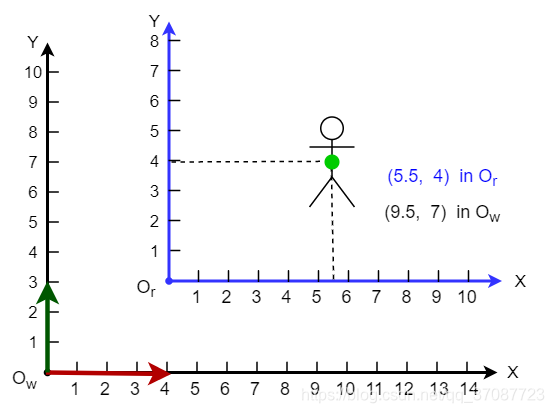
在这里插入图片描述
目标在两个坐标系下的位置关系如下:

旋转变换

在这里插入图片描述
这里的小车坐标系可以认为是由世界坐标系通过逆时针旋转了θ角度而来，此时θ为正值。当然，也可以认为世界坐标系是由小车坐标系顺时针旋转θ角而来。根据几何或向量相关知识

详细推导
在这里插入图片描述

对于向量而言，无论在A坐标系还是B坐标系，他的方向和模长是没有变的，只是观测者不同
在这里插入图片描述
两边同时乘以 $i_a$ 向量,得到在由B变换到A坐标系的x坐标,y坐标同理

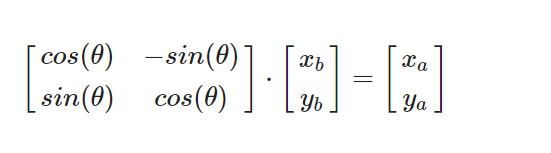
其中的 2x2 矩阵我们称之为旋转矩阵，并且只有旋转的角度θ有关，此矩阵有两个意义：

该旋转矩阵描述了从一个坐标系到另一个坐标系的变换（逆时针旋转θ为正，顺时针旋转θ为负）
旋转后的坐标系中的某一点通过左乘此旋转矩阵，可以得到其在旋转之前坐标系下的坐标

旋转+平移变换

在这里插入图片描述
详细推导

在这里插入图片描述

3D坐标变换

右手定则

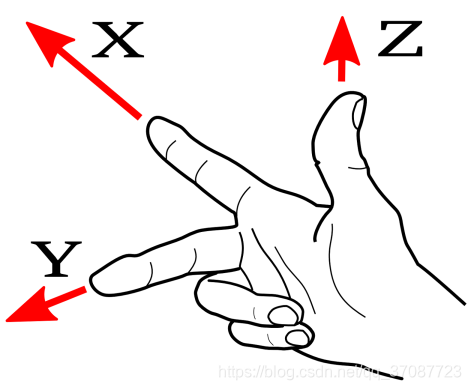
在这里插入图片描述
坐标系的旋转

坐标系的旋转角度为正值时，我们从外侧看向坐标轴，其旋转方向应为逆时针。
坐标系的旋转角度为负值时，我们从外侧看向坐标轴，其旋转方向应为顺时针。

旋转变换

单独旋转某轴

X轴
在这里插入图片描述
y轴

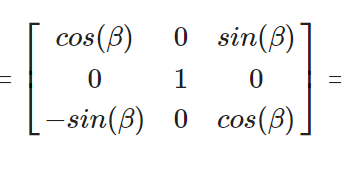
z轴

通过矩阵转换为
i-x axis
j-y axis
k-z axis

在三维空间中，旋转可以通过三个欧拉角 $(\alpha ,\beta ,\gamma )$ 来定义。有一些可能的欧拉角定义，每个都可以依据 roll, pitch 和 yaw 的复合来表达。依据 “x-y-z” 欧拉角，在右手笛卡尔坐标中的旋转矩阵可表达为:
${\mathcal {M}}(\alpha ,\beta ,\gamma )={\mathcal {R}}_{z}(\gamma ){\mathcal {R}}_{y}(\beta ){\mathcal {R}}_{x}(\alpha )$

在这里插入图片描述

3D姿态的描述方式

旋转矩阵

在这里插入图片描述

优点
方便矩阵的变换计算
其形式直观的描述了变换后的坐标系三个轴在变换前坐标系下的向量
缺点
参数过多，一个矩阵就有9个变量，包含三个角度每个角的sin和cos值，共6个单位数据
表述不够清晰易懂，无法了解变换过程

欧拉角 & RPY

欧拉角是由Leonhard Euler 引入的，用于描述刚体方向的三个角，在3维欧几里得空间中描述这样一个方向，需要三个参数。欧拉角是一种更加通用及实用的旋转方式，其特点是绕运动的坐标轴旋转，即每次旋转，都是绕着运动变化后的自身坐标轴进行旋转。由于其旋转轴是绕自身坐标系的，又称之为内旋（Intrinsic Rotation）

假如两个坐标系A和B重合，那么将坐标系B绕自身Z轴旋转α，然后绕自身Y轴旋转β，最后绕自身X轴旋转γ，此时其旋转矩阵的计算方式为连续右乘，如下
在这里插入图片描述
欧拉角是用来表示三维坐标系中方向和方向变换的。欧拉角其实还可以细分为欧拉角(Euler-angles)和泰特布莱恩角(Tait-Bryan-angles)，这两种方法都利用了笛卡尔坐标系的三轴作为旋转轴，主要区别在于旋转轴的选取顺序。
在这里插入图片描述
欧拉角的旋转轴选取顺序有（x,y,x）(x,z,x)……共6种，其选取顺序是a,b,a的顺序，也就是绕a轴旋转某角度后，绕新生成的b轴旋转一个角度，最后绕两次旋转以后的a轴再旋转一个角度，以此表示最终的方向。
泰特布莱恩角的旋转轴选取有（x,y,z）(x,z,y)……也就是历遍笛卡尔坐标系的三轴，比如我们最常见到的Roll-Pitch-Yaw角等同于其中的（z,y,x）顺序

RPY

左静右动
RPY是Roll翻滚（绕X），Pitch俯仰（绕Y），Yaw偏航（绕Z）的缩写，即如我们所讲到的旋转示例，先绕X轴旋转 γ度、接着绕Y轴旋转 β度、最后绕Z轴旋转 α 度。这里的每一步旋转，都是绕着固定的坐标系进行旋转的。由于其旋转轴是绕固定坐标系的，又称之为外旋（Extrinsic Rotation）
假如两个坐标系A和B重合，那么将坐标系B绕A坐标系的X轴旋转γ，然后绕A坐标系的Y轴旋转β，最后绕A坐标系的 Z轴旋转α，此时其旋转矩阵的计算方式为连续左乘，如下：
在这里插入图片描述

万向节死锁

pitch不能为90度，否则会发生万向节死锁
“死锁”一词具有误导性：我们并没有限制万向架。所有三个万向节仍然可以围绕各自的悬架轴自由旋转。然而，由于两个万向架的轴相对平行，所以没有可用的万向架来适应围绕指定一个轴的旋转。
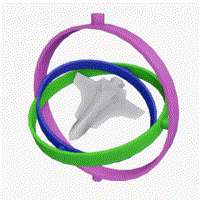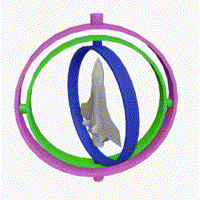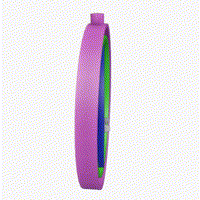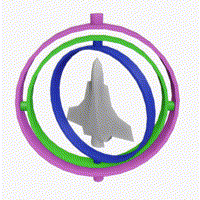
请添加图片描述
万向节（Gimbal）为一个有枢纽的装置，它使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架，可使架在最里部环架的物体维持旋转轴不变，其应用在船上的陀螺仪、罗盘、饮料杯架等用途，而不受船体因波浪上下震动、船身转向的影响

如何避免万向节死锁？

在欧拉角的12中旋转顺序中选择适合场景的方式
可以使用四元数的方式计算旋转。

四元数

对比 https://quaternions.online/
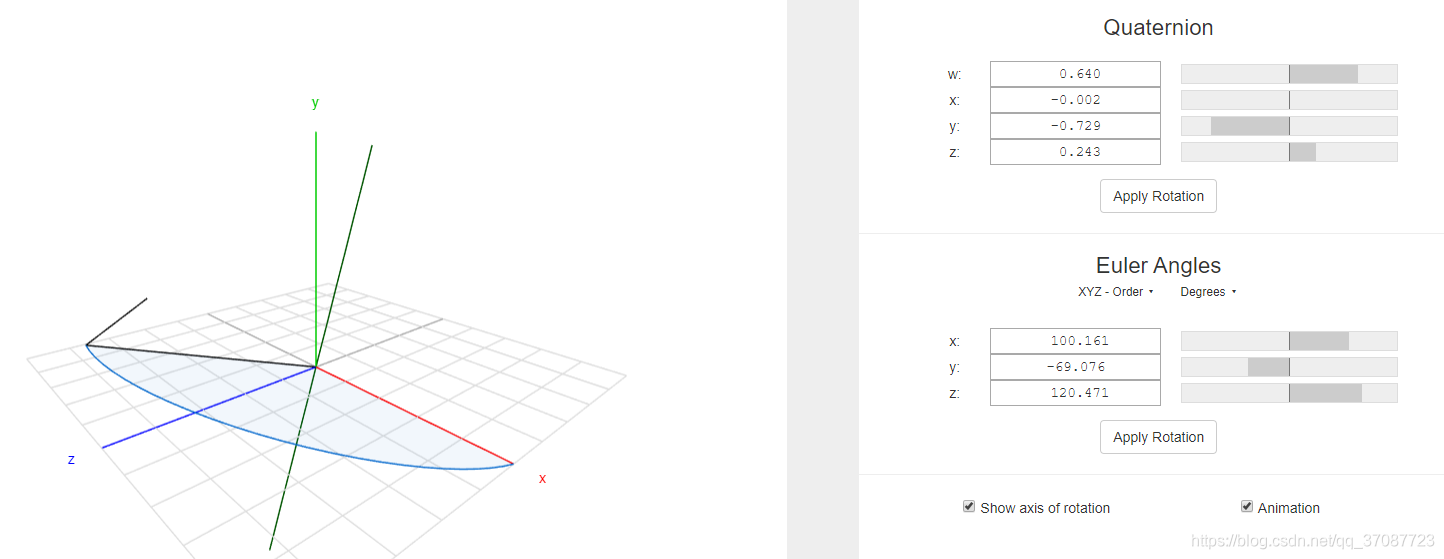
在这里插入图片描述

由于欧拉角的数值变换为非线性的，计算过程会产生奇异值，则为了从数学上避免类似万向节死锁的问题。我们使用四元数可以帮助四轴飞行器更好的旋转，避免“翻车”。

Y

四元数存储了旋转轴和旋转角的信息，它能方便的描述刚体绕任意轴的旋转。其形式为：

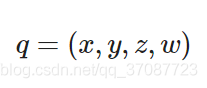
$x^2+y^2+z^2+w^2=1$

缺点：

数据不够直观
运算比较复杂

四元数的与旋转矩阵互转

已知四元数 $q = (x, y, z, w)$
在这里插入图片描述
euler->rotation

其他描述方式

除了以上的旋转矩阵、欧拉角、RPY、四元数，在编程过程中，还会有以下两种格式，这里不做展开。
轴角对（Axis-angle）：可以和四元数直接互转

任意的旋转都可以用一个旋转轴和绕轴的旋转角来描述，简称“轴角”（Axis-Angle）；
轴为：n
角为：theta
则，对应的四元数中的w、x、y、z的值分别为：
w = cos(theta / 2)
x = nx * sin(theta / 2) // nx 是轴 n 的 x 分量
y = ny * sin(theta / 2) // ny 是轴 n 的 y 分量
z = nz * sin(theta / 2) // nz 是轴 n 的 z 分量

旋转向量（Rotation Vector）：可以和旋转矩阵通过罗德里格斯公式（Rodrigues’s Formula）相互转换

旋转向量，是一个三维向量，其方向与旋转轴一致，长度等于旋转角；

多种姿态转换：https://www.andre-gaschler.com/rotationconverter/

旋转矩阵求解

sin-> S; cos->C
在这里插入图片描述

求解a

b求解

化简完成后，发现一个结论:

γ 求解

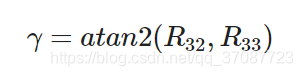
奇异值情况求解

这里根据以下值是否等于0（小于一个阈值）来判断此时的旋转矩阵是否是奇异矩阵，如果是奇异矩阵，则结果有所差异
在这里插入图片描述
如果cos(B)=0或接近零，说明其在 Pitch轴为90°，此时产生万向节死锁，求解方式有所差异，具体如下

在这里插入图片描述

"""
依次绕着X,Y,Z固定轴旋转变换矩阵
"""
import numpy as np
from math import sin, cos,atan2
def merge(R,T):
    Tr=np.eye(4,dtype=R.dtype)
    Tr[:3,:3]=R
    Tr[:3,3]=T# is 3 no 4
    return Tr

#保留三位小数，不使用科学技术法
np.set_printoptions(precision=3,suppress=True)


def euler2R(theta,format="degree"):


    if format=="degree":
        theta=np.deg2rad(theta)
    a, b, r = theta
    Rx = np.array([
        [1, 0, 0],
        [0, cos(a), -sin(a)],
        [0, sin(a), cos(a)]
    ])
    R_y = np.array([
        [cos(b), 0, sin(b)],
        [0, 1, 0],
        [-sin(b), 0, cos(b)],
    ])
    R_z = np.array([
        [cos(r), - sin(r), 0],
        [sin(r), cos(r), 0],
        [0, 0, 1],
    ])

    return R_z@R_y@Rx

def is_rotation_matrix(R):
    Rt=np.transpose(R)
    Is=R@Rt
    I=np.identity(3,dtype=R.dtype)
    n=np.linalg.norm(I-Is)
    return  n<1e-6

def R2euler(R):
    #    # 旋转矩阵：正交矩阵 （转置==逆） （矩阵 @ 矩阵的逆 == I单位矩阵）
    assert (is_rotation_matrix(R))
    # 旋转矩阵：正交矩阵 （转置==逆） （矩阵 @ 矩阵的逆 == I单位矩阵）
    sy=np.sqrt(R[0,0]**2+R[1,0]**2)
    singlar=sy<1e-6# 判断是否是奇异矩阵
    if singlar==0:
        z=atan2(R[1,0],R[0,0])
        y=atan2(-R[2,0],sy)
        x=atan2(R[2,1],R[2,2])
    else:
        z=0
        y=atan2(-R[2,0],sy)
        x=-atan2(R[1,2],R[1,1])
    return np.array([x,y,z])

if __name__ == '__main__':
    # 输入参数，x，y，z角度
    R=euler2R((30,20,33))

    print(R)
    theta=R2euler(R)
    print(np.rad2deg(theta))

    t=np.array([1 ,0 ,2])
    Tr=merge(R,t)
    print(Tr)

实例

待定

案例：https://robot.czxy.com/car/coordinate/pose_demo/
参考
https://robot.czxy.com/car/coordinate/transform2d/
https://zh.wikipedia.org/wiki/%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5#%E6%97%8B%E8%BD%AC
https://zhuanlan.zhihu.com/p/93563218

明码

关注

1
点赞
踩
8

收藏

觉得还不错? 一键收藏
0
评论
坐标转换+程序

文章目录2D世界与小车坐标系示例¶平移变换旋转变换旋转+平移变换3D坐标变换右手定则旋转变换单独旋转某轴3D姿态的描述方式旋转矩阵欧拉角 & RPYRPY万向节死锁如何避免万向节死锁？四元数Y缺点：四元数的与旋转矩阵互转其他描述方式旋转矩阵求解2D世界与小车坐标系示例¶为什么我们要获取目标在不同的坐标系下的位姿呢？我们通过以下的简单案例进行讲解并计算。假如在一个世界坐标系下有一个小车和一个人，则很容易看出来他们两个在世界坐标系下的位置。但事实上，我们通常能通过小车的摄像头或雷达等传感器，
复制链接

扫一扫