此学习笔记来自于王燕老师编著的《时间序列分析-基于R》
对一个时间序列预处理后检验出该序列为平稳时间序列说明该模型有提取信息的价值,就要进行下一步的模型建立来拟合该模型然后做出预测。下面介绍拟合时间序列的三个重要模型。
一、AR模型
AR(p)模型得简记形式如下,其中p为自回归阶数。
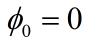
对于模型的拟合介绍两种最常用的拟合函数分别为arima.sim函数拟合与filter函数拟合,arima.sim函数可以拟合平稳AR序列、MA序列、平稳ARMA序列以及ARIMA序列。函数命令如下:
arima.sim(n, list(ar=,ma=,order=),sd=)
# n:拟合序列长度
# list:指定具体参数模型参数,其中:
(1)拟合平稳AR(p)模型,要给出自回归系数,如果指定拟合AR模型为非平稳模型,系统会报错。
(2)拟合MA(q)模型,要给出移动平均系数。
(3)拟合平稳ARMA(p,q)模型,需要同时给出自回归系数和移动平均系数,如果指定模型为非平稳系统会报错。
(4)拟合ARIMA(p,d,q)模型,除了需要给出自回归系数和移动平均系数,还需要增加order选项,order=c(p,d,q),其中p为自回归系数,d为差分阶数,q为移动平均数。
# sd:指定序列的标准差,默认sd=1. filter函数可以直接拟合AR序列(无论是否平稳)和MA序列。函数命令如下:
filter(e,filter=,method=,circular=)
# e:随机波动序列变量名。
# method:指定拟合的是AR模型还是MA模型。
(1)method="recursive"为AR模型;
(2)methid="convolution"为MA模型。
# circular:拟合MA模型时专用的一个选项,circular=T可以避免NA数据出错。
以下面四个模型为例,先考察它们的平稳性:
x1<-arima.sim(n=100,list(ar=0.8))
x3<-arima.sim(n=100,list(ar=c(1,-0.5)))
e<-rnorm(100)
x2<-filter(e,filter = -1.1,method = "recursive")
x4<-filter(e,filter = c(1,0.5),method = "recursive")
ts.plot(x1)
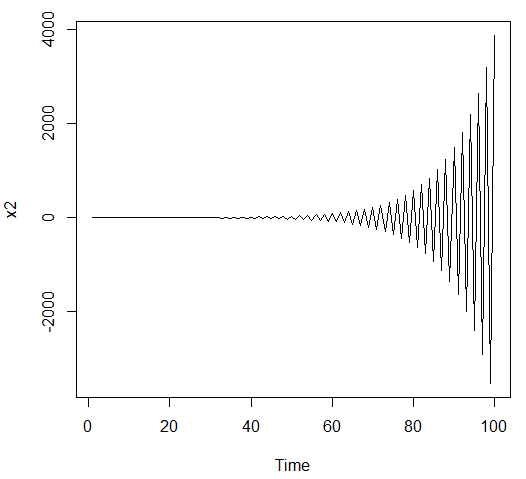
ts.plot(x2)
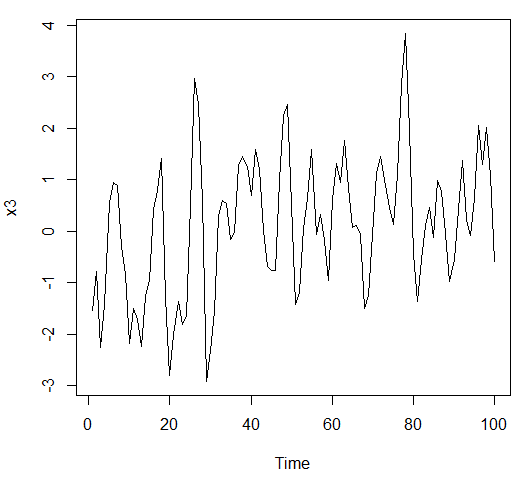
ts.plot(x3)
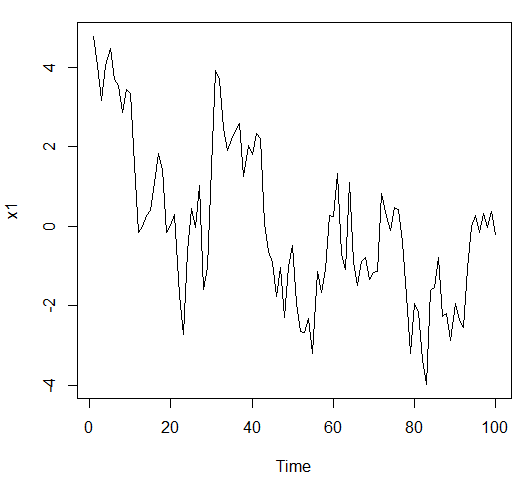
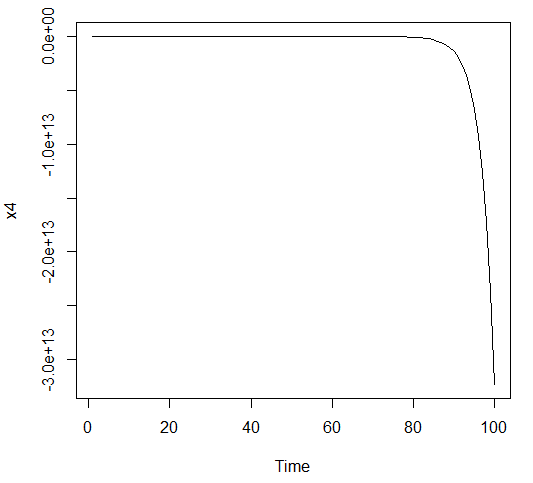
ts.plot(x4)结果如下所示:
根据图形可以判断x1和x3模型为平稳序列,x2和x4模型为非平稳序列(x2和x4模型用arima.sim函数拟合时也会报错,说明该序列非平稳,要用filter函数拟合)。图示法是一种直观但是粗糙的判别方法,接下来介绍精确两种平稳性判别方法:特征根判别与平稳域判别。
特征根判别AR模型为平稳的充要条件为:
平稳域判别AR模型平稳的充要条件为:
以上四个模型根据特征根和平稳域判别如下:
平稳AR(P)模型的自相关系数具有拖尾性和呈指数衰减的两个显著性质。
以上面(1)和(3)平稳AR模型为例:
x1<-arima.sim(n=1000,list(ar=0.8))
x3<-arima.sim(n=1000,list(ar=c(1,-0.5)))ts.plot(x1)
ts.plot(x3)
acf(x1)
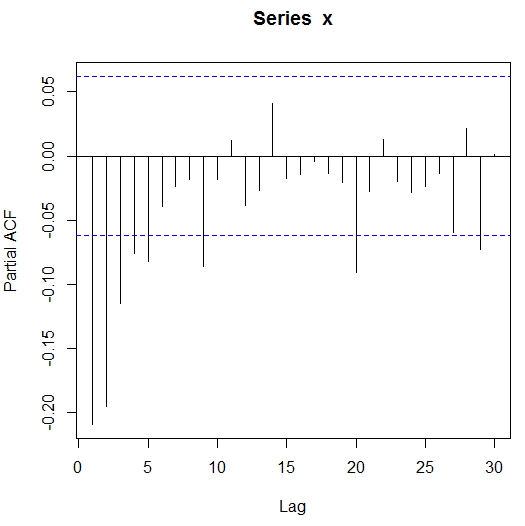
acf(x3) 从图形可以看出不管是AR(1)模型还是AR(2)模型,无论它们是正根或是负根,它们的自相关系数都呈拖尾性和指数衰减到零的性质。 平稳AR(P)模型的偏自相关系数具有P步截尾性。 同样以上面(1)和(3)平稳AR模型为例:pacf(x1)
pacf(x3) 由于样本随机性,样本自相关系数不会和理论偏自相关系数一样严格截尾,但从图形看出AR(1)模型的样本偏自相关系数1阶显著不为零,1阶以后都近视为零;AR(2)模型的样本偏自相关系数2阶显著不为零,2阶以后都近视为零,样本自相关图直观验证了AR模型偏自相关系数的截尾性。二、MA模型
MA(q)(q为移动最高阶数)模型的简记模型如下: 时为中心化MA(q)模型。 MA(q)模型具有q阶截尾的性质,下面以四个模型为例: x1<-arima.sim(n=1000,list(ma=-2))
x2<-arima.sim(n=1000,list(ma=-0.5))
x3<-arima.sim(n=1000,list(ma=c(-4/5,16/25)))
x4<-arima.sim(n=1000,list(ma=c(-5/4,25/16)))
acf(x1)
acf(x2)
acf(x3)
acf(x4) 样本自相关图清晰显示MA(1)模型自相关系数1阶截尾,MA(2)模型自相关系数2阶截尾的特征。 MA(q)模型具有偏自相关系数拖尾性:pacf(x1)
pacf(x2)
pacf(x3)
pacf(x4) 从偏自相关图看出无论MA(1)模型或是MA(2)模型得偏自相关系数具有不同形式的拖尾性。三、ARMA模型
中心化RAMA(p,q)模型简写为:
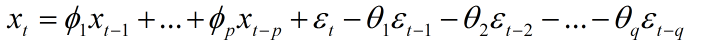
当q=0时,RAMA(p,q)模型就退化成了AR(p)模型;
当p=0时,RAMA(p,q)模型就退化成了MA(q)模型;
RAMA(p,q)模型具有自相关系数不截尾,偏自相关系数也不截尾的性质。
以下面ARMA(1,1)模型为例:
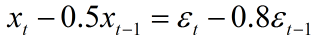
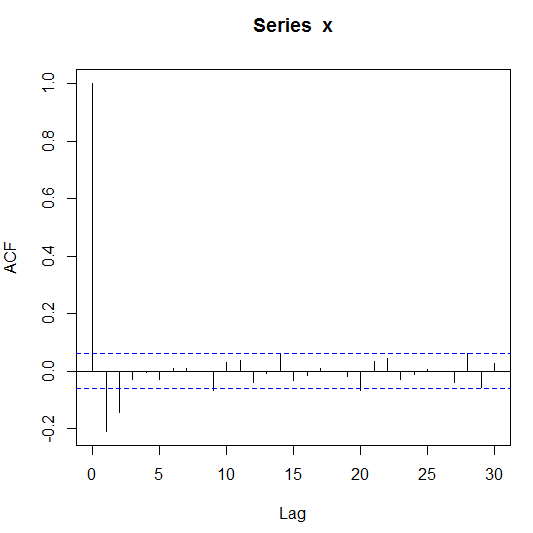
综合AR(p)模型,MA(q
)模型和ARMA(p,q)模型自相关系数和偏自相关系数的性质得出如下规律:









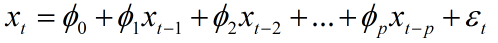
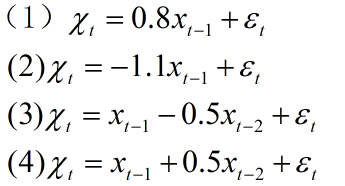
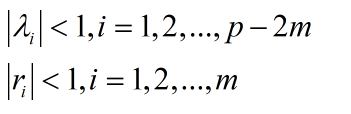
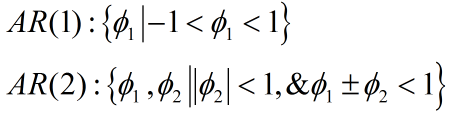















 2340
2340

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








