数据结构——快速排序

各种排序情况：

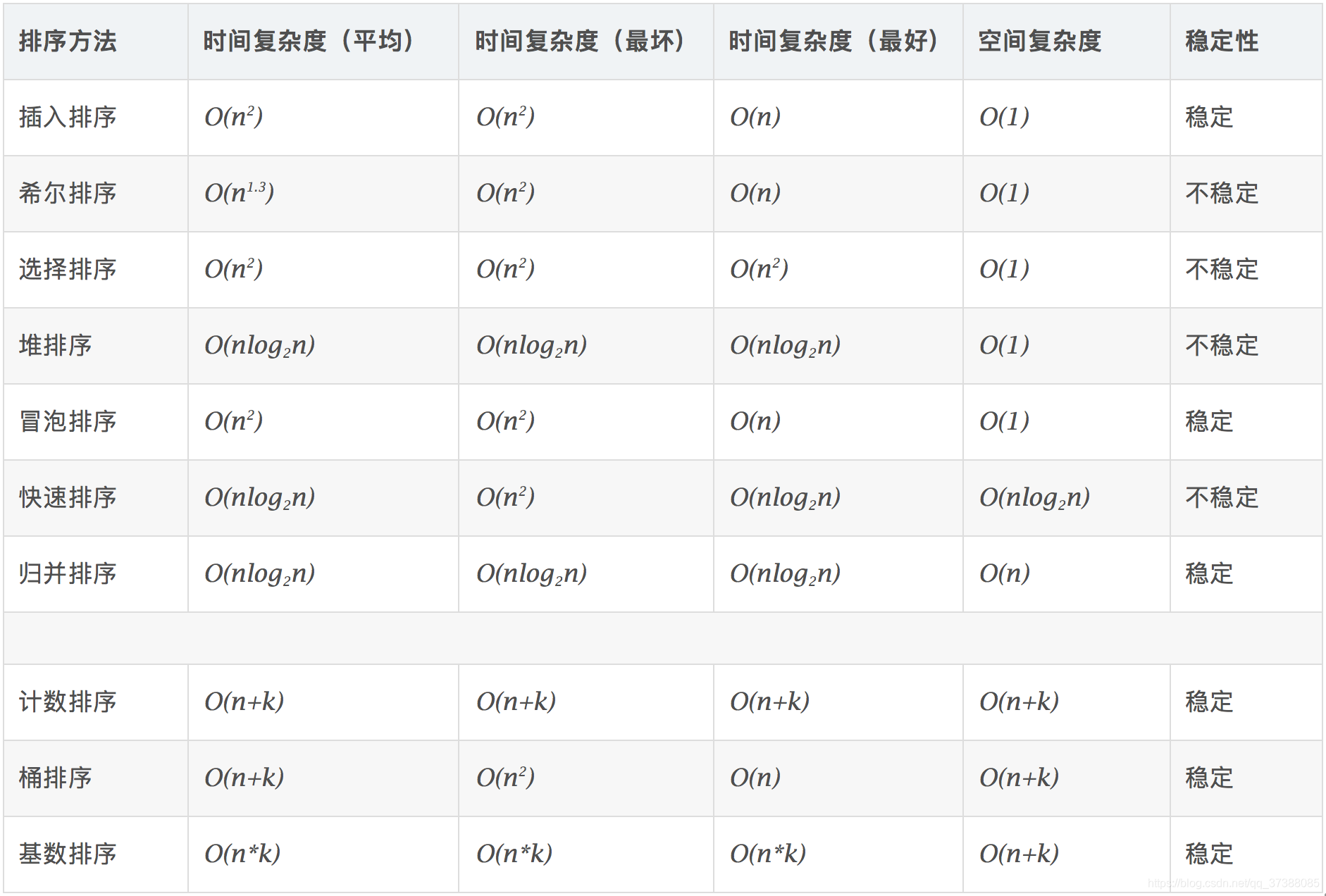
• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

1. 快速排序

1.1 基本思想

跨苏排序英文Quick Sort，是冒泡排序的一种改进，由C.A.R.Hoare在1960年提出，快速排序的主要思想是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据逗笑，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使得整个数据变为有序序列；

原理

1. 在数据集之中，选择一个元素作为“基准”；
2. 所有小于“基准”的元素，都移动到“基准”左边，所有大于“基准”的元素，都移动到“基准”右边，这个操作称为分区；
3. 分区操作结束后，基准元素所在的位置就是最终排序后它的位置；
4. 对“基准”左边和右边两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止；

对于包含n个数的输入数组来说，快速排序是一种最坏情况时间复杂度为$O(n^2)$的排序算法。虽然最坏情况时间复杂度很高，但是快速排序通常是实际排序应用中最好的选择，因为它的平均性能很好；它的期望时间复杂度是$O(nlgn)$，而且$O(nlgn)$中隐含的常数因子非常小。另外，它还能够进行原址排序。

与归并排序一样，快速排序使用了分治思想。下面是对一个典型的子数组A[p…r]进行快速排序的三步分治过程；

分治：数组A[p…r]被划分为两个（可能为空）子数组A[p…q-1]和A[q+1…r]，使得A[p…q-1]中的每一个元素都小于等于A[q]，而A[q]也小于等于A[q+1…r]中的每个元素。其中，计算下标q也是划分过程的一部分。
解决：通过递归调用快速排序，对子数组 A[p…q-1]和A[q+1…r]进行排序。
合并：因为子数组都是原址排序的，所以不需要合并操作：数组A[p…r]已经有序。

下面的程序实现快速排序：

QUICKSORT(A，p，r)
if p < r
    q = PARTITION(A, p, r)
    QUICKSORT(A, p, q-1)
    QUICKSORT(A, q+1, r)

为了排序一个数组A的全部元素，初始调用是QUICKSORT(A, 1, A.length)

数组的划分
算法的关键部分是PARTITION过程，它实现了对子数组A[p…r]的原址重排。

PARTITION(A, p, r)
x = A[r]
i = p-1
for j = p to r-1
    if A[j] <= x
        i = i+1
        exchange a[i] with A[j]
exchange A[i+1] with A[r]
return i+1

1.1 快速排序的性能

快速排序的运行时间依赖于划分是否平衡，而平衡与否又依赖于用于划分的元素。如果划分是平衡的，那么快速排序算法性能与归并排序一样。如果划分是不平衡的，那么快速排序的性能接近于插入排序。

最坏情况划分-时间复杂度
当划分产生的两个子问题分别包含n-1个元素和0个元素时，快速排序的最坏情况发生了。不妨假设算法的每一次递归调用中都出现了这种不平衡划分。划分操作的时间复杂度是$\theta (n)$。由于对一个大小为0的数值进行递归调用会直接返回，因此T(0)=$\theta (1)$，于是算法运行时间的递归式可以表示为：$$T(n)=T(n-1)+T(0)+\theta (n)=T(n-1)+\theta (n)$$通过这个递归公式可以知道最坏情况下的时间复杂度为$\theta (n^2)$。

因此，如果在算法的每一层递归上，划分都是最大程度不平衡的，那么算法的时间复杂度就是$\theta (n^2)$。也就是说，在最坏情况下，快速排序算法的运行时间并不比插入排序更好。此外，当输入数组已经完全有序时，快速排序的时间复杂度仍然为$\theta (n^2)$。而在同样情况下，插入排序的时间复杂度为$O(n)$。

最好情况划分-时间复杂度
在可能的最平衡的划分中，PARTITION得到的两个子问题的规模都不大于n/2，这是因为其中一个子问题的规模为$\lfloor n/2\rfloor$，而另一个子问题的规模为$\lceil n/2\rceil -1$。在这种情况下，快速排序的性能非常好。此时，算法运行时间的递归式为：$$T(n)=2T(n/2)+\theta (n)$$在上式中，我们忽略了一些余项以及减1操作的影响。上述递归式的解为$T(n)=\theta (nlgn)$。快速排序的平均运行时间更接近于其最好情况，而非最坏情况。

空间复杂度
快速排序的空间复杂度为O(lgn)，因为快速排序是在原址上进行排序的，所以主要是递归是产生的空间消耗。n个元素进行二分需要lgn次才能划分完毕，因此需要存储迭代产生的消耗是2lgn，因此空间复杂度为O(lgn)。

1.2 快速排序的随机化版本

在快速排序中采用一种称为随机抽样的随机化技术，与始终采用A[r]作为主元的方法不同，随机抽样是从子数组A[p…r]中随机选择一个元素作为主元。为达到这一目的，首先将A[r]与从A[p…r]中随机选出的一个元素交换。通过对序列p,…,r的随机抽样，我们可以保证主元元素x=A[r]是等概率地从子数组的r-p+1个元素中选取的。

对PARTITION和QUICKSORT的代码的改动非常小。在新的划分程序中，我们只是在真正进行划分前进行一次交换：

RANDOMIZED-PARTITION(A, p, r)
i = RANDOM(p, r)
exchange A[r] with A[i]
return PARTITION(A, p, r)

新的快速排序不再调用PARTITION，而是调用RANDOMIZED-PARTITION：

RANDOMIZED-QUICKSORT(A, p, r)
if p < r
    q = RANDOMIZED-PARTITION(A, p, r)
    RANDOMIZED-QUICKSORT(A, p, q-1)
    RANDOMIZED-QUICKSORT(A, q+1, r)

1.3 快速排序算法实现

• python版本

def quick_sort(collection):
    length = len(collection)
    if length <= 1:
        return collection
    else:
        pivot = collection.pop()  # 将collection中的最后一个数字弹出
        greater, lesser = [], []
        for element in collection:  # 进行二分
            if element > pivot:
                greater.append(element)
            else:
                lesser.append(element)
        return quick_sort(lesser) + [pivot] + quick_sort(greater)


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()  # strip()的作用是移除字符串头尾指定的字符
    unsorted = [int(item) for item in user_input.split(",")]
    print(quick_sort(unsorted))

• python版本

def quick_sort_3partition(sorting, left, right):
    if right <= left:
        return
    a = i = left
    b = right
    pivot = sorting[left]
    while i <= b:
        if sorting[i] < pivot:
            sorting[a], sorting[i] = sorting[i], sorting[a]
            a += 1
            i += 1
        elif sorting[i] > pivot:
            sorting[b], sorting[i] = sorting[i], sorting[b]
            b -= 1
        else:
            i += 1
    quick_sort_3partition(sorting, left, a - 1)
    quick_sort_3partition(sorting, b + 1, right)


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    quick_sort_3partition(unsorted, 0, len(unsorted) - 1)
    print(unsorted)

• C++版本

#include <iostream>
#include<vector>
using namespace std;


int PARTITION(vector<int>& arr,int begin, int end)
{
    int temp = arr[end];
    int i = begin - 1;
    for(int j=begin;j<end;++j)
    {
        if(arr[j] <= temp)
        {
            i++;
            swap(arr[i],arr[j]);
        }
    }
    swap(arr[i+1],arr[end]);
    return i+1;
}

void QUICK_SORT(vector<int>& arr, int begin, int end )
{
    if(begin < end) {
        int temp = PARTITION(arr, begin, end);
        QUICK_SORT(arr, begin, temp - 1);
        QUICK_SORT(arr, temp + 1, end);
    }
}

int main() {
    vector<int> arr;
    int num;
    int n;
    while(cin>>num )  //输入eof结束
    {
        arr.push_back(num);
        n++;
    }
    QUICK_SORT(arr,0,n-1);
    for (int i = 0; i < arr.size(); i++) {
        cout << arr[i] << ",";
    }
    return 0;
}