HW2(1) 四足狗单足平衡点寻找与LQR平衡控制率

HW2(1) 四足狗单足平衡点寻找与LQR平衡控制率

题目需求

本问题利用我们所学的平衡点的知识和基础的无约束优化的方法来寻找单足机械臂平衡点（理论上从不同的初始值开始，可以找到许多不同的平衡点），所用的机械狗为宇树A1。而后利用找到的平衡点，在平衡点线性化并设计线性LQR控制器来使机械狗在平衡点周围能收敛到平衡点。

流程：

• 平衡点寻找
  • 平衡点处的KKT条件
  • 牛顿法迭代求解平衡点
  • 平衡点稳定性分析
• 平衡点稳定
  • Riccati Recursion求解LQR控制器
  • LQR闭环控制
  • 无限/有限时域LQR的增益对比
  • 未控/受控系统稳定性分析
  • 仿真结果

平衡点寻找

系统模型以及模型雅可比和Hessian矩阵的求解调用Julia的RigidBodyDynamics求解（可以读URDF），其中状态$x$为30维，输入$u$为12维。

给定系统的初始状态$x_{guess}$，通过以下代码求解雅可比

model = UnitreeA1()	# 这个类是在另一个文件实现的，主要是一些包装，核心是利用RigidBodyDynamics求雅可比
x_guess = initial_state(model)	# 设定的初始状态
u = zeros(12)	# 求输入为0下的平衡点
xdot = dynamics(model, x_guess, u)	# 连续时间动力学
∇f = jacobian(model, x_guess, u)	# 连续时间雅可比
norm(xdot) # 结果是217.37，因此这个初始点不是平衡点

KKT条件

给定一个初始估计，我们将寻找最近的平衡点的任务构建成下面所述的带等式约束的非线性优化问题
$$\begin{gathered} {\text{minimize}}_{x,u}\frac{1}{2}(x-x_{\text{guess}}{)}^T(x-x_{\text{guess}})+0.5e^{-3}{u}^{T}u \\ \text{subject to}f(x,u)=0 \end{gathered}$$
因此，可以根据这个优化问题写出它的KKT条件（极小值点的一阶必要条件）（推导过程详见HW1(0)）

function kkt_conditions(model::UnitreeA1, x, u, λ, A, B)
    ∇ₓL = (x - x_guess) + A' * λ #梯度向量
    ∇ᵤL = 1e-3 * u + B' * λ
    c = dynamics(model, x, u)
    # Return the concatenated vector
    return [∇ₓL; ∇ᵤL; c]
end

为了求解这个KKT条件对应的状态，可以使用牛顿法，但是使用牛顿法时，需要对KKT条件求雅可比矩阵并把$A$看成是$A(x)$，因为$A(x)$本身就是动力学方程的梯度，假如再对$A(x)$再求一次梯度的话，就是对动力学方程求二阶导，代价是非常大的。因此我们采用高斯牛顿近似，把$A(x)$看成$A$，相当于把模型线性化了，全局的梯度都是$A$，与$x$无关，再对$A$求雅可比就为0了。

function kkt_jacobian(model::UnitreeA1, x, u, λ, A, B, ρ=1e-3)
    H = zeros(2n+m, 2n+m)	# n是状态维度，m是输入维度。
    H[1:n,1:n] = I(n)
    H[n+1:n+m,n+1:n+m]=1e-3*I(m)	# 具体推导参考HW1(0)
    H[1:n,n+m+1:m+2*n] = A'
    H[n+1:n+m,n+m+1:m+2*n] = B'
    H[n+m+1:2*n+m,1:n] = A
    H[n+m+1:2*n+m,n+1:n+m] = B
    
    H_reg = H	# 正则化过程，对前n+m维加上正值，后n维减去正值，详见Lecture 5 
    Reg = ρ * Diagonal([ones(n+m); -ones(n)])
    H_reg = H_reg + Reg		# 理论上高斯牛顿法的KKT系统的Hessian一定是半正定的，不需要Regularization
    return Symmetric(H_reg) # 但是实际由于一些舍入误差\截断误差，小小正则化一下可以有更好的数值效果
end

迭代求解

迭代求解过程就是一个局部二次化（求解A B），然后写出KKT条件并得到KKT系统的Hessian矩阵，然后根据Hessian矩阵进行迭代。由于是高斯牛顿法，因此不一定需要正则化（当然加了更好），并且从结果中可以很显然看出，因为没有加线搜索的步骤，在某些步数处会有超调，导致KKT残差的上升。

迭代过程KKT残差变化

平衡点位置

function newton_solve(model::UnitreeA1, x_guess, mvis=nothing; verbose=true, max_iters=50, ρ=1e-3)
    u = zeros(12)	# U的初始值选为0
    x = deepcopy(x_guess) 	# X初始值给定
    λ = zeros(x_guess)	# λ初始值也是全0
    iter = 0
    res_hist = Float64[]
    α = 1
	println("Iter:     || Res:    ")
    while iter ≤ max_iters && res_norm > 1e-6
        println("      $iter         $res_norm")
        ∇f = jacobian(model, x, u)
        A = ∇f[1:n,1:n]
        B = ∇f[1:n,n+1:n+m]
        res = kkt_conditions(model::UnitreeA1, x, u, λ, A, B)
        res_norm = norm(res)
        res_hist = [res_hist res_norm]        
        H = kkt_jacobian(model::UnitreeA1, x, u, λ, A, B)
        Δz = -H\res		# Z是KKT系统全部的变量，由x u λ stack而成
        Δx = Δz[1:n]	
        Δu = Δz[n+1:n+m]
        Δλ = Δz[n+m+1:2*n+m]
        x  .= x + α * Δx
        u  .= u + α * Δu
        λt .= λ + α * Δλ

        iter = iter + 1
    end
    return x,u,λ, res_hist
end

平衡点稳定性分析

因为本节用的是连续时间的动力学方程，因此求平衡点处的雅可比矩阵，判断是否所有的特征值是否小于0。

这里分析的是没有控制器情况下，系统是不是稳定的，后文还会继续分析，有LQR控制器之后的。

∇f = jacobian(model, xstar, ustar)
A = ∇f[1:n,1:n]
eigs = eigvals(A) # 30个特征值，有些大于0，有些小于0
norm(eigs,Inf) # 57.41，大于0，所以是不稳定的

平衡点稳定控制率

与前文不同，为了设置离散时间LQR控制率，得对系统的动力学方程进行离散化（RK4）。

model = UnitreeA1()
∇f = discrete_jacobian(RK4, model, xeq, ueq, dt)
A = ∇f.A # 在平衡点离散化，认为整个系统都是线性系统
B = ∇f.B

Riccati Recursion

通过Riccati equation反向迭代，求得所有时刻最优反馈控制矩阵。

function riccati(A,B,Q,R,Qf,N)
    # initialize the output
    P = [zeros(n,n) for k = 1:N]
    K = [zeros(m,n) for k = 1:N-1]
    P[end] .= Qf	# 末端的Cost-to-go函数V(x)已知
    for k = reverse(1:N-1) #时不变LQR与时变LQR的区别就是A与A[k]
        K[k] .= (R + B'P[k+1]*B)\(B'P[k+1]*A)	# 反馈控制矩阵
        P[k] .= Q + A'P[k+1]*A - A'P[k+1]*B*K[k]# Cost-to-Go矩阵
    end
    return K,P
end

闭环LQR控制率

function get_control(controller::LQRController, x, t)
    t_k = get_k(controller,t)	# 得到此时t对应的离散点t_k
    if controller.infinite_horizon == true
        Gain = controller.K[1]  # 无限时域的LQR则取一个常值的K矩阵，一般K[1]是收敛后了的 
    else
        Gain = controller.K[t_k]# 有限时域的LQR则取一个变化的K 
    end
    u = controller.ueq - Gain * (x - controller.xeq) # 反馈控制率
    return u
end

分析有限时域LQR控制率的K矩阵，发现在2s的时间窗口内，LQR控制率的K能基本收敛，在4s的窗口内，可以看到$K$很明显的收敛现象。

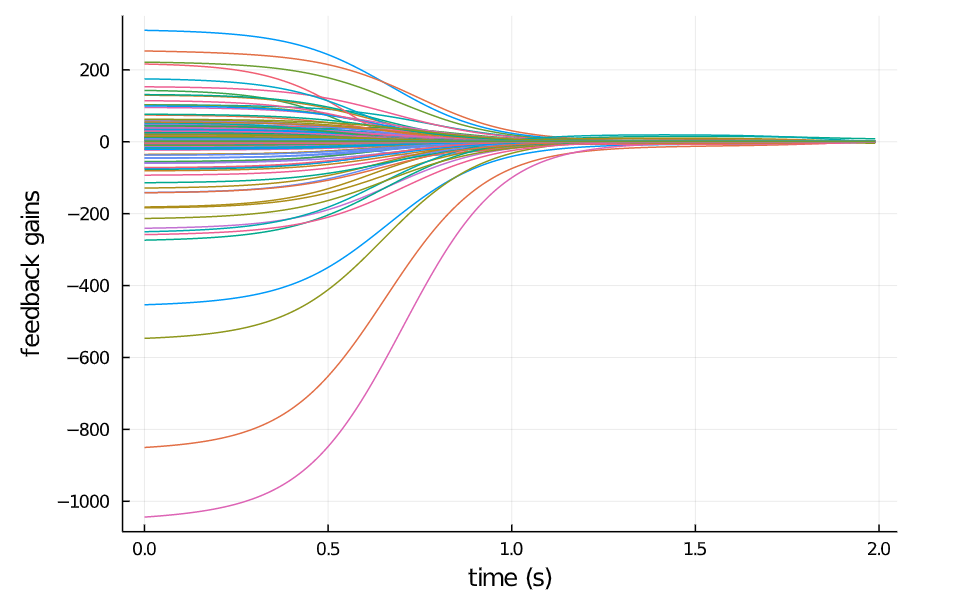
闭环系统稳定性分析

加了LQR控制器后，闭环系统方程变成了$A-BK$，此时再分析系统的特征值，可以发现LQR闭环系统是稳定的。

stability0 = maximum(norm.(eigvals(A)))  # 1.62 > 1
stability = maximum(norm.(eigvals(A-B*K[1]))) # 0.99 < 1

仿真结果

分别选取Horizon为2和4进行有限时域和无限时域系统的仿真，得到如下结果，从结果中我们可以看出（虚线为无限时域的）

• 在本stablization问题上，无限时域的LQR性能表现比有限时域的要好，甚至在H=2s时，有限时域的LQR系统不是稳定的，后面会倒下去
• 在时间窗口取得比较长的时候如H=4，两者的表现是类似的
• 无限时域的LQR的控制量会比有限时域的要大一些，原因应该是在$K$未收敛的时间段，越往后则反馈矩阵$K$越小，会使系统慢慢不稳定。

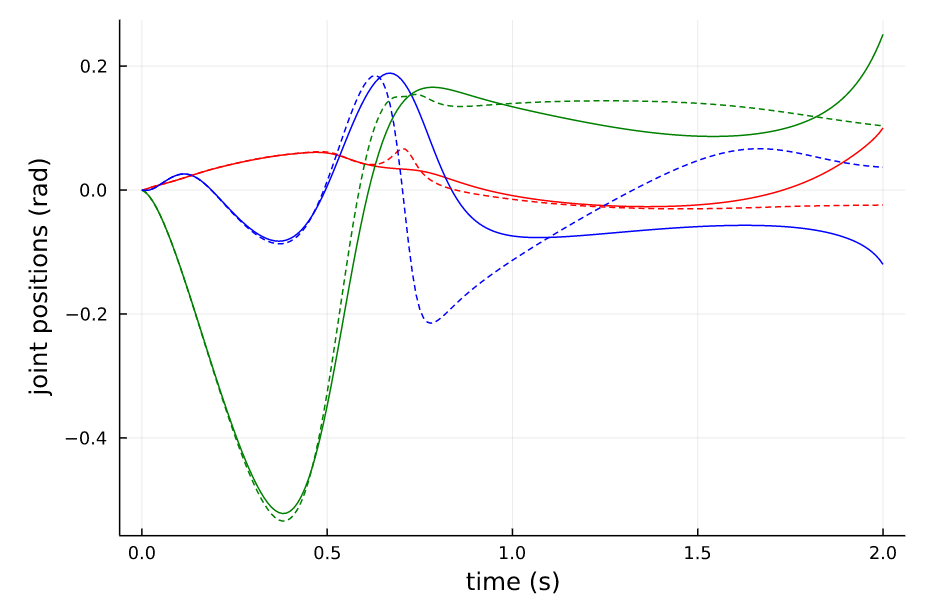
Horizon=2 有限时域与无限时域LQR 状态	Horizon=2 有限时域与无限时域LQR 控制
Horizon=4 有限时域与无限时域LQR 状态	Horizon=4 有限时域与无限时域LQR 控制

Horizon=2 有限时域LQR	Horizon=2 无限时域LQR
Horizon=4 有限时域LQR	Horizon=4 无限时域LQR