文章介绍了线性二次调节器（LQR）的三种解法：间接法、打靶法和Riccati迭代。LQR问题涉及最小化系统状态和输入的加权平方和。间接法通过极小值原理求解，打靶法需要初始控制轨迹，而Riccati迭代则通过递推计算得到最优反馈控制率。案例分析表明，Riccati迭代在处理有限时间LQR问题时，能提供稳定的反馈控制，即使在有噪声或不确定性的情况下，也能使系统收敛到平衡点。此外，无限时域LQR通常使用常值反馈矩阵K进行系统稳定化。
Leture 7 LQR（Linear Quadratic Regulator）的三种解法
目录
- 间接法（indirect method）、打靶法（shooting method）
- 二次规划QP解法
- Riccati迭代(Riccati Recursion)
有限时间LQR问题
考虑离散时间有限时间窗口LQR问题
minx1:N,u1:N−1∑k=1N−1[12xkTQkxk+12ukTRkuk]+12xNTQNxN ∋ xk+1=Akxk+Bkuk(1)
\begin{align}
\min_{x_{1:N}, u_{1:N-1}} &\sum_{k=1}^{N-1} \Big[ \frac{1}{2} x_k^T Q_k x_k + \frac{1}{2} u_k^T R_k u_k \Big] + \frac{1}{2} x_N^T Q_N x_N \\
& \ \ni \ x_{k+1} = A_k x_k + B_k u_k
\end{align}\tag{1}
x1:N,u1:N−1mink=1∑N−1[21xkTQkxk+21ukTRkuk]+21xNTQNxN ∋ xk+1=Akxk+Bkuk(1)
其中，Q是半正定的，R是正定。
- 问题的目标是使系统的状态回到原点（如倒立摆中，将倒立摆的角度与角速度变成0）
- 假如R不是正定的，如R等于零矩阵，那么控制器要做的就是，把输入拉到无穷大，从而使状态瞬时回到原点，这个问题是病态的，因此R要是正定的。
- 假如Ak=A,Bk=B,Qk=Q,Rk=R ∀ kA_k=A, B_k=B, Q_k=Q, R_k=R \ \forall \ kAk=A,Bk=B,Qk=Q,Rk=R ∀ k，是一个时不变LQR，否则是一个时变LQR(Time-Variant TVLQR)问题。
- 一般地，时不变LQR用于将系统状态转移回平衡点，时变LQR用于跟随轨迹
- LQR可以用于局部近似许多非线性问题，在这些问题局部使用LQR可以取得一个不错的效果
- 有许多种LQR的扩展，如无限时域LQR，随机LQR(stochastic LQR).
- 被叫做，控制理论的皇冠明珠（It’s been called the crown jewel of control theory）
shooting/indirect法
将LQR问题(1)代入Lecture 6 (9)中得到的极小值原理结果中有，
xk+1=Axk+Bukλk=Qxk+ATλk+1, λN=QxNuk=−R−1BTλk+1 (2)
\begin{align}
x_{k+1} &= A x_k + B u_k \\
\lambda_k &= Q x_k + A^T \lambda_{k+1}, \ \lambda_N = Q x_N \\
u_{k} &= -R^{-1} B^T \lambda_{k+1} \
\end{align}\tag{2}
xk+1λkuk=Axk+Buk=Qxk+ATλk+1, λN=QxN=−R−1BTλk+1 (2)
用shooting法解LQR的步骤与Lecture 6中写的相似，要有一条初始的控制轨迹uuu，进行rollout得到所有xxx，而后从λN\lambda_NλN开始backward pass得到所有λ\lambdaλ，最后可以代入得到新的控制轨迹uuu直至收敛。
案例分析
考虑一个双积分器系统，
x˙=[q˙q¨]=[0 10 0][qq˙]+[01]u(3)
\begin{align}
\dot{x} = \begin{bmatrix}
\dot{q} \\
\ddot{q}
\end{bmatrix}
=
\begin{bmatrix}
0 \ \ 1 \\
0 \ \ 0
\end{bmatrix}
\begin{bmatrix}
q \\
\dot{q}
\end{bmatrix}
+
\begin{bmatrix}
0 \\
1
\end{bmatrix}
u
\end{align}\tag{3}
x˙=[q˙q¨]=[0 10 0][qq˙]+[01]u(3)
这个系统我们可以精确离散化成，
xk+1=[1 h0 1][qkqk˙]+[12h2h]uk(4)
\begin{align}
x_{k+1} =
\begin{bmatrix}
1 \ \ h \\
0 \ \ 1
\end{bmatrix}
\begin{bmatrix}
q_k \\
\dot{q_k}
\end{bmatrix}
+
\begin{bmatrix}
\frac{1}{2} h^2 \\
h
\end{bmatrix}
u_k
\end{align}\tag{4}
xk+1=[1 h0 1][qkqk˙]+[21h2h]uk(4)
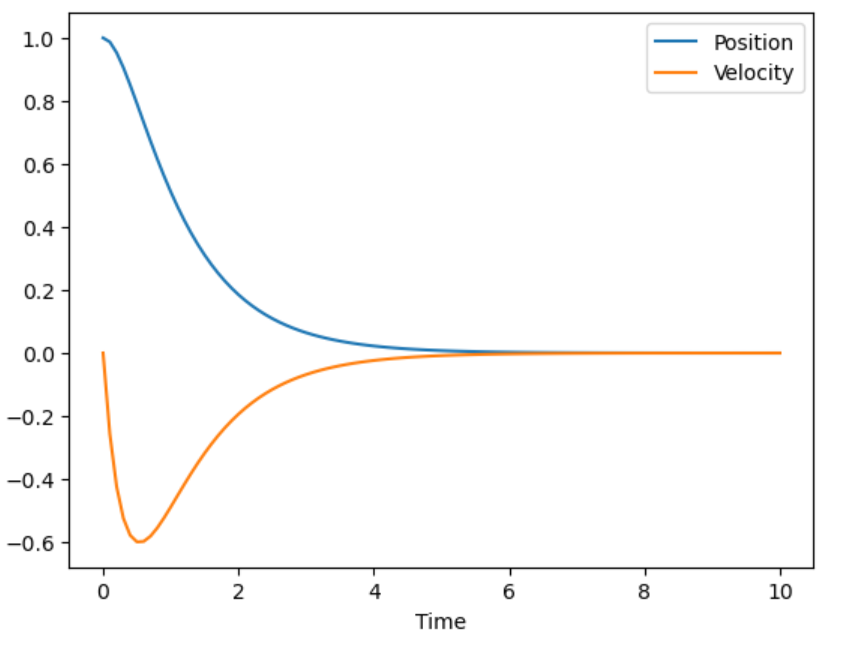
shooting状态轨迹 |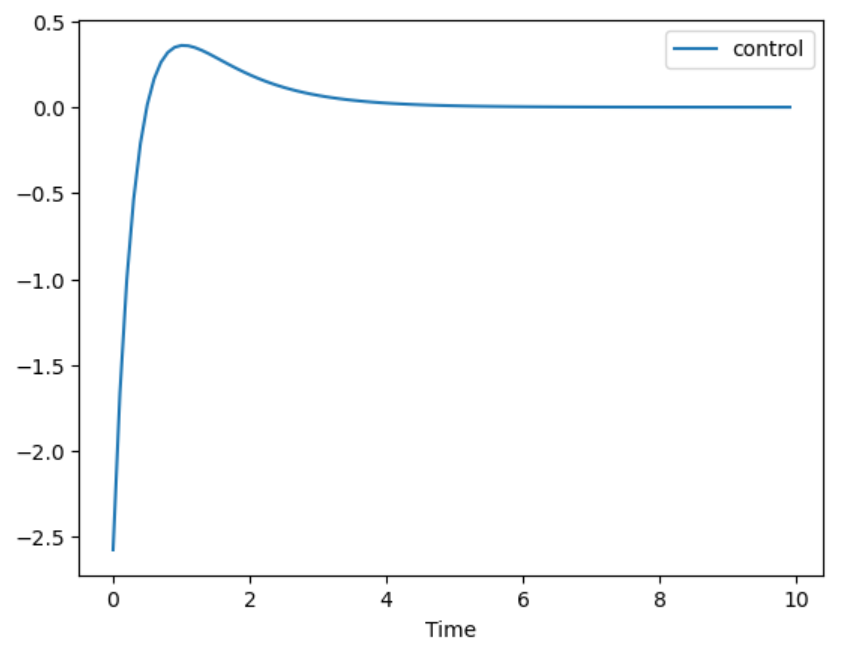 
shooting输入轨迹 |
在我的笔记本中，运行直接通过极小值原理导出的shooting法在时间为10s，离散化100个点时，需要迭代2400次，耗时17s，如果把时间调成20s，跑了4分钟都没出结果。这说明这种最原始的方法速度是比较慢的（不是说所有shooting方法都不好，比如DDP本质上也是一个shooting方法，但是基于动态规划的迭代比这种迭代方式高效）。
# Initial guess
xhist = repeat(x0, 1, N)
uhist = zeros(N-1) # u(t)的初始估计必须的. Shooting法中不需要x(t)的估计
Δu = ones(N-1)
λhist = zeros(n,N)
xhist = rollout(xhist, uhist) #initial rollout to get state trajectory
J(xhist,uhist) #Initial cost 50左右，final cost大概是6
b = 1e-2 #line search tolerance 为了更好的结果应该要调参
α = 1.0
iter = 0
while maximum(abs.(Δu[:])) > 1e-2 #terminate when the gradient is small
#Backward pass to compute λ and Δu
λhist[:,N] .= Qn*xhist[:,N]
for k = N-1:-1:1
Δu[k] = -(uhist[k]+R\B'*λhist[:,k+1]) # 即使是本身线性系统，迭代法求出的还是Δu。
λhist[:,k] .= Q*xhist[:,k] + A'*λhist[:,k+1]
end
#Forward pass with line search to compute x
α = 1.0
unew = uhist + α.*Δu
xnew = rollout(xhist, unew)
while J(xnew, unew) > J(xhist, uhist) - b*α*Δu[:]'*Δu[:] # 这个armijo的选择Δu感觉，应该要调参
α = 0.5*α # backtrack
unew = uhist + α.*Δu
xnew = rollout(xhist, unew)
end
uhist .= unew;
xhist .= xnew;
iter += 1
end
QP解法
对于(1)中的LQR问题，我们把所有未知变量叠成一个大向量zzz(x1x_1x1已知，不是决策变量)
z=[u1x2u2..xN](5)
\begin{align}
z = \begin{bmatrix}
u_1 \\
x_2 \\
u_2 \\
. \\
. \\
x_N
\end{bmatrix}
\end{align}\tag{5}
z=u1x2u2..xN(5)
然后定义HHH阵，
H=[R10...00Q2...0 . 00...QN](6)
\begin{align}
H = \begin{bmatrix}
R_1 & 0 & ... & 0 \\
0 & Q_2 & ... & 0 \\
\ & \ & . & \ \\
0 & 0 & ... & Q_N
\end{bmatrix}
\end{align}\tag{6}
H=R10 00Q2 0..........00 QN(6)
则有，J=12zTHzJ=\frac{1}{2} z^T H zJ=21zTHz,接着定义
C=[B1(−I)............00AB(−I)......0 . 00......AN−1BN−1(−I)]d=[−A1x10.0](7)
\begin{align}
C &= \begin{bmatrix}
B_1 & (-I) & ... & ... &...& ... & 0 \\
0 & A & B & (-I) &...& ... & 0 \\
\ & \ & . & \ \\
0 & 0 & ... &...& A_{N-1} & B_{N-1} & (-I)
\end{bmatrix} \\
d &= \begin{bmatrix}
-A_1 x_1 \\
0 \\
. \\
0
\end{bmatrix}
\end{align}\tag{7}
Cd=B10 0(−I)A 0...B.......(−I) .........AN−1......BN−100(−I)=−A1x10.0(7)
则整个LQR问题可以变成一个带有等式约束的QP标准问题
minz12zTHz ∋Cz=d(8)
\begin{align}
&\min_{z} \frac{1}{2} z^T H z \\
\ &\ni C z = d
\end{align}\tag{8}
zmin21zTHz∋Cz=d(8)
该问题的KKT条件为：
∇zL=Hz+CTλ=0∇λL=Cz−d=0(9)
\begin{align}
\nabla_z L &= H z + C^T \lambda = 0 \\
\nabla_{\lambda} L &= C z - d = 0
\end{align}\tag{9}
∇zL∇λL=Hz+CTλ=0=Cz−d=0(9)
可以解析地写出该二次问题的解（不需要迭代，就类似一个二次函数求根问题，导数为0只有一个点，这个点对于一个凸问题来说，一定是个全局最小值点）
[HCTC0][zλ]=[0d](10)
\begin{align}
\begin{bmatrix}
H & C^T \\
C & 0
\end{bmatrix}
\begin{bmatrix}
z \\
\lambda
\end{bmatrix}
&=
\begin{bmatrix}
0 \\
d
\end{bmatrix}
\end{align}\tag{10}
[HCCT0][zλ]=[0d](10)
案例分析
同样的，我们使用QP来解同样的LQR问题，在取得同样的结果的情况下，QP花了0.4ms，并且获得了一样的最终cost。
H = blockdiag(R, kron(I(N-2), blockdiag(Q,R)), Qn);#Kronecker积，与I相乘相当于复制那么多份
# Constraints
C = kron(I(N-1), [B -I(2)])
for k = 1:N-2
C[(k*n).+(1:n), (k*(n+m)-n).+(1:n)] .= A
end
d = [-A*x0; zeros(size(C,1)-n)];
# Solve the linear system
y = [H C'; C zeros(size(C,1),size(C,1))]\[zeros(size(H,1)); d]
相比于shooting法，用QP法或者Riccati Recursion都不需要一个初始的控制率u
Riccati Recursion
将LQR问题转化成QP问题之后，问题变成了求线性方程(10)的解，而由于方程10所表示的KKT系统的结构特殊，并且是稀疏的，我们将其展开，推导更为高效的求解方法。
首先，将(10)展开有（考虑N=4），
[R .BT Q .−IAT R .BT Q .−IAT R.BT QN.−I..........B−I .000 AB−I .000 AB−I.000][u1x2u2x3u3x4λ2λ3λ4]=[000000−Ax100](11)
\begin{align}
\begin{bmatrix}
R & \ & \ & \ & \ & & . & B^T & & \\
\ & Q & \ & \ & \ & & . & -I & A^T & \\
\ & \ & R & \ & \ & & . & & B^T & \\
\ & \ & \ & Q & \ & & . & & -I & A^T \\
\ & \ & \ & \ & R & & . & & & B^T \\
\ & \ & \ & \ & \ & Q_N & . & & & -I \\
. & . & . & . & . & . & . & . & . & . \\
B & -I & \ & \ & \ & \ & . & 0 & 0 & 0 \\
\ & A & B & -I & \ & \ & . & 0 & 0 & 0 \\
\ & \ & \ & A & B & -I & . & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
u_1 \\
x_2 \\
u_2 \\
x_3 \\
u_3 \\
x_4 \\
\lambda_2 \\
\lambda_3 \\
\lambda_4
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
-A x_1 \\
0 \\
0
\end{bmatrix}
\end{align}\tag{11}
R .B Q .−IA R . B Q . −IA R . BQN. −I..........BT−I.000ATBT−I.000ATBT−I.000u1x2u2x3u3x4λ2λ3λ4=000000−Ax100(11)
考虑左上块的最后一行，将它单独写出来，
QNx4−λ4=0 ⟹ λ4=QNx4(12)
\begin{align}
Q_N x_4 - \lambda_4 &= 0
\implies \lambda_4 = Q_N x_4
\end{align}\tag{12}
QNx4−λ4=0⟹λ4=QNx4(12)
再把左上块的倒数第二行写出，
Ru3+BTλ4=Ru3+BTQNx4=0(13)
\begin{align}
R u_3 + B^T \lambda_4 &= R u_3 + B^T Q_N x_4 = 0
\end{align}\tag{13}
Ru3+BTλ4=Ru3+BTQNx4=0(13)
将系统动力学代入，消掉x4x_4x4，
Ru3+BTQN(Ax3+Bu3)=0 ⟹ u3=−(R+BTQNB)−1BTQNAx3(14)
\begin{align}
R u_3 + B^T Q_N (A x_3 + B u_3) &= 0
\implies u_3 = - (R + B^T Q_N B )^{-1} B^T Q_N A x_3
\end{align}\tag{14}
Ru3+BTQN(Ax3+Bu3)=0⟹u3=−(R+BTQNB)−1BTQNAx3(14)
定义x3x_3x3前面那一大块叫做K3=(R+BTQNB)−1BTQNAK_3=(R + B^T Q_N B )^{-1} B^T Q_N AK3=(R+BTQNB)−1BTQNA.
再把左上块的倒数第三行写出,
Qx3−λ3+ATλ4=0(15)
\begin{align}
Q x_3 - \lambda_3 + A^T \lambda_4 = 0
\end{align}\tag{15}
Qx3−λ3+ATλ4=0(15)
要消掉λ4\lambda_4λ4获得λ3\lambda_3λ3的表达式，先把系统方程代入，再代入(14)得到的反馈控制率，
Qx3−λ3+ATQNx4=0 ⟹ Qx3−λ3+ATQN(Ax3+Bu3)=0 ⟹ Qx3−λ3+ATQN(A−BK)x3=0 ⟹ λ3=(Q+ATQN(A−BK))x3(16)
\begin{align}
Q x_3 - \lambda_3 + A^T Q_N x_4 &= 0 \\
\implies Q x_3 - \lambda_3 + A^T Q_N (A x_3 + B u_3) &= 0 \\
\implies Q x_3 - \lambda_3 + A^T Q_N (A - B K) x_3 &= 0 \\
\implies \lambda_3 = (Q + A^T Q_N (A- BK)) x_3
\end{align}\tag{16}
Qx3−λ3+ATQNx4⟹Qx3−λ3+ATQN(Ax3+Bu3)⟹Qx3−λ3+ATQN(A−BK)x3⟹λ3=(Q+ATQN(A−BK))x3=0=0=0(16)
最后，定义P3=(Q+ATQN(A−BK))P_3 = (Q + A^T Q_N (A- BK))P3=(Q+ATQN(A−BK)),得到整个系统的Riccati递归方程
PN=QNKn=(R+BTPn+1B)−1BTPn+1APn=Q+ATPn+1(A−BKn)(17)
\begin{align}
P_N &= Q_N \\
K_n &= (R + B^T P_{n+1} B)^{-1} B^T P_{n+1} A \\
P_n &= Q + A^T P_{n+1} (A - BK_n)
\end{align}\tag{17}
PNKnPn=QN=(R+BTPn+1B)−1BTPn+1A=Q+ATPn+1(A−BKn)(17)
结合(14)(16)(17)三条式子，Riccati recursion的流程可以如此解读：先从terminal cost开始反向迭代，求出系统所有的Kn PnK_n \ P_nKn Pn，从表达式可以看出，这几个值只跟系统的问题定义有关（状态方程和Q R），与初始状态无关。而(14)(16)的值都是与xnx_nxn直接相关的（un=−Knxn λn=Pnxnu_n=-K_nx_n \ \lambda_n=P_nx_nun=−Knxn λn=Pnxn），而xnx_nxn是由x1x_1x1rollout得到的。
因此，在得到LQR系统所有的Kn PnK_n \ P_nKn Pn后，对于任意一个不同的初始状态x1x_1x1,均可以由(14)得到的反馈控制率代入，即可得到最优控制的结果。这相比Shooting法和QP法是很有优势的。
- 通过Riccati方程解LQR的方式的时间复杂度是O(N(n+m)3)\mathcal{O} (N (n+m)^3)O(N(n+m)3)(NNN是离散点数，n mn \ mn m是状态和输入维度)，因为我们只需要对小矩阵求逆，而通过QP式子(10)解LQR问题的时间复杂度是O(N3(n+m)3)\mathcal{O} (N^3 (n+m)^3)O(N3(n+m)3)，因为要对一个很大的矩阵求逆（所以大部分时候要想QP或者SQP快，就得利用矩阵的稀疏特性，在商业求解器中如SNOPT就是如此做的）
- 更重要的是，这种方式可以得到一个最优反馈控制率
案例分析
同样地，使用Riccati迭代来求解LQR问题。有点奇怪的是，在我的电脑中，实际上Riccati的方式运行地比QP慢，可能是julia自带的矩阵求逆有做了优化。
使用迭代好的反馈控制率KnK_nKn,
(1)我们尝试从一个任意的起始状态出发看看控制率能否使系统收敛
(2)尝试在系统方程中加入噪声或不确定性
结果如下，可以看出，通过Riccati方式解LQR得到的反馈控制率即使在有噪声或者其他状态启动，均能使系统最终收敛到平衡点，这是非常好的性质。
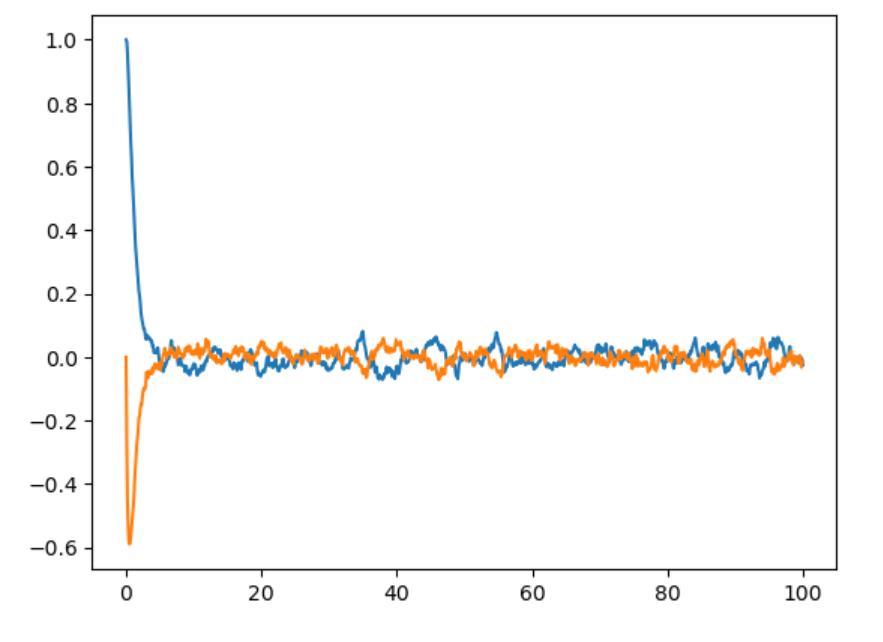
Riccati控制率（加系统噪声） |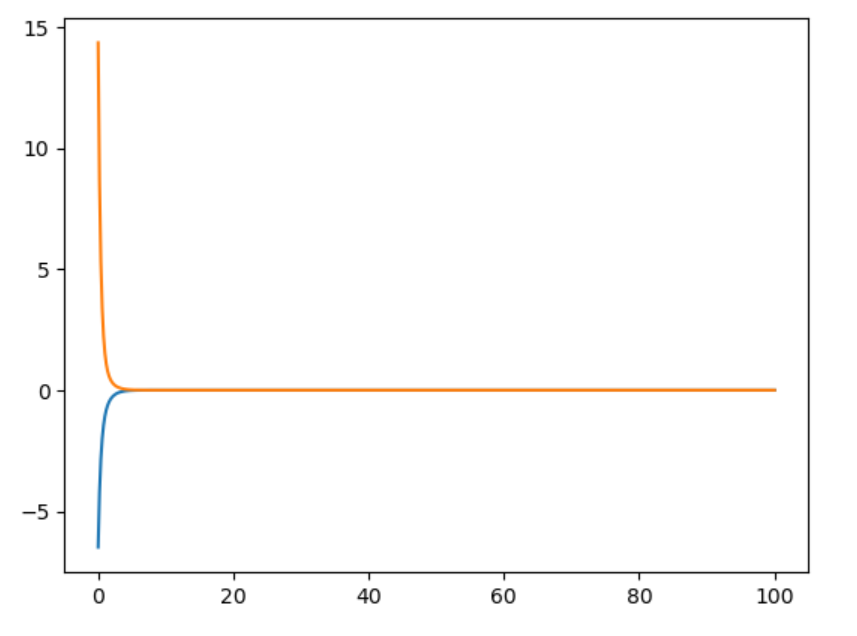 
Riccati控制率（任意起始位置） |
再分析Riccati收敛后得到的控制率KnK_nKn 每一步的值，可以发现，K的值很快就收敛到了一个常值，而这个常值，也对应着无限时域LQR所得到的最优反馈矩阵KKK。我们使用Julia自带的dlqr函数对本系统进行求解，得到反馈矩阵的值为[2.5857,3.4434]，与图中的收敛值一样。因此，一般在使系统稳定时（stablization problem），使用一个常值的KKK（当作infinite horizon LQR）.
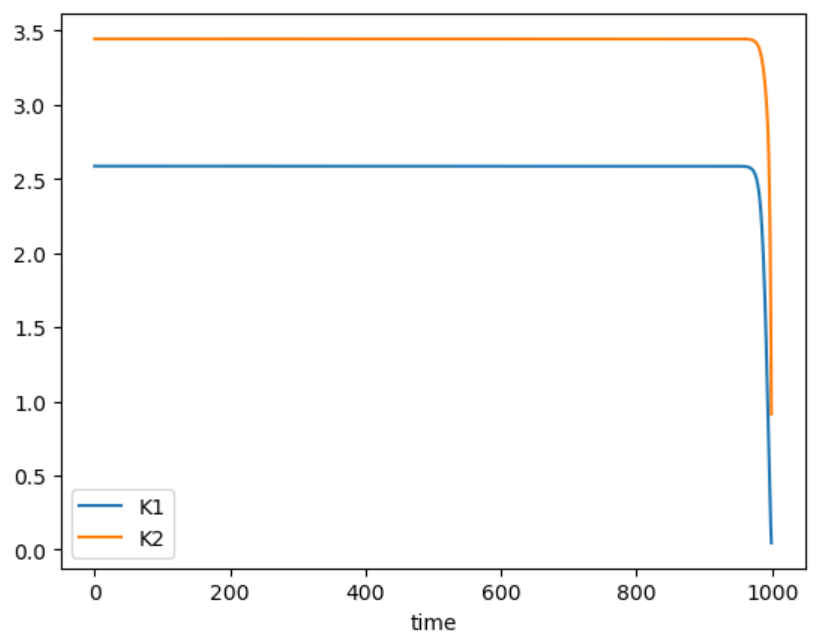
Riccati 控制率K_n矩阵值 |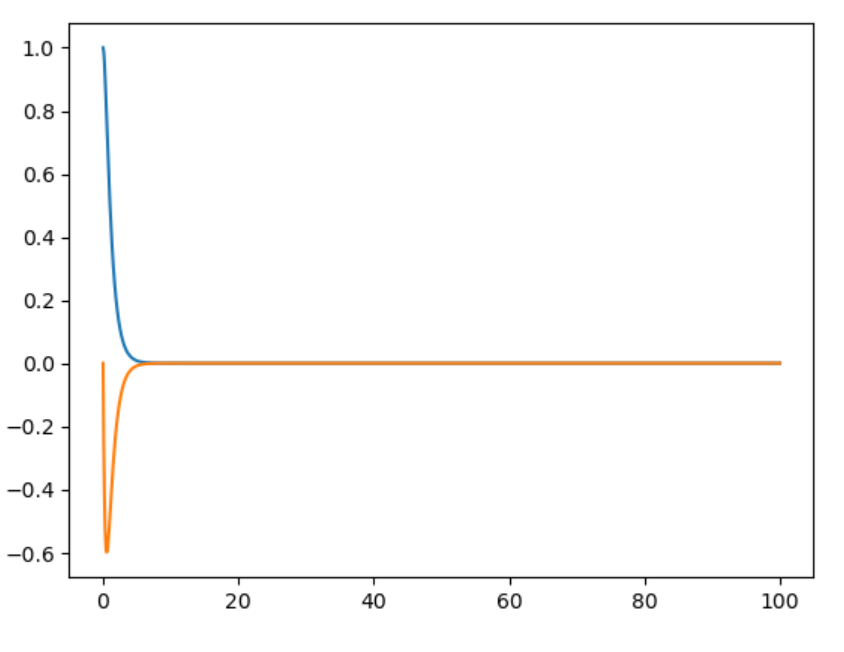 
常值K矩阵控制结果 |
P = zeros(n,n,N)
K = zeros(m,n,N-1)
P[:,:,N] .= Qn
#Backward Riccati recursion
for k = (N-1):-1:1
K[:,:,k] .= (R + B'*P[:,:,k+1]*B)\(B'*P[:,:,k+1]*A)
P[:,:,k] .= Q + A'*P[:,:,k+1]*(A-B*K[:,:,k])
end
#Forward rollout starting at x0
xhist = zeros(n,N)
xhist[:,1] = x0 # randn(2)*10
uhist = zeros(m,N-1)
for k = 1:(N-1)
uhist[:,k] .= -K[:,:,k]*xhist[:,k] #根据得到的反馈控制率求u
xhist[:,k+1] .= A*xhist[:,k] + B*uhist[k] + 0.01*randn(2) #can add noise to dynamics
end
无限时域LQR
从案例分析中看出，对于一个有限时域N的LQR系统来说，矩阵KKK在backward pass反向迭代的过程中，经过一段时间就很快收敛到常值了。因此，
- 对于一个无限时域的LQR系统，求出来的KKK会是一个常数矩阵
- 对于stabilization问题，一般我们直接使用这个常值矩阵KKK,假如在MATLAB或者Julia中调用LQR的函数，返回的就是一个最优反馈控制率KKK（在本节中，实际是一个最优的PD控制器）
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
