深度学习策略调研

已于 2022-09-19 15:58:54 修改
阅读量922 收藏 4
点赞数 2
于 2021-01-05 10:47:57 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_37534839/article/details/110816993
版权

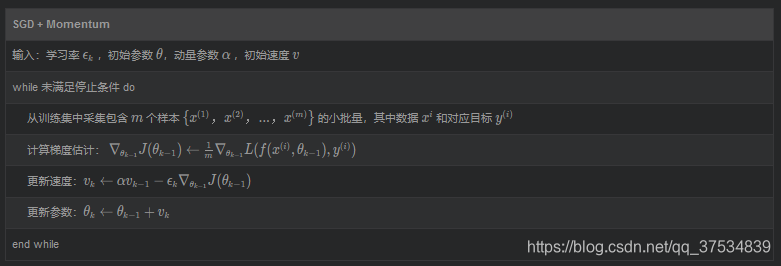
学习器

SGD

https://blog.csdn.net/kuweicai/article/details/102997831
在这里插入图片描述

学习策略

ReduceLROnPlateau

当一个指标停止改进时降低学习率。

  • optimizer
  • mode (str): One of min, max
  • factor (float): Factor by which the learning rate will be reduced
  • patience (int): Number of epochs with no improvement after which learning rate will be reduced.
  • cooldown (int): Number of epochs to wait before resuming normal operation after lr has been reduced.
        >>> optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9, weight_decay=5e-4)
        >>> scheduler = ReduceLROnPlateau(optimizer,mode='max', factor=0.1, patience=4, cooldown=0)
        >>> for epoch in range(10):
        >>>     train(...)
        >>>     val_loss = validate(...)
        >>>     scheduler.step(val_loss)

CyclicLR

https://arxiv.org/abs/1506.01186
https://arxiv.org/pdf/1708.07120.pdf
https://arxiv.org/pdf/1908.06477.pdf
在这里插入图片描述

  • base_lr (float or list) : lower boundary
  • max_lr (float or list) : upper boundary
  • step_size_up (int) – Number of training iterations in the increasing half of a cycle. Default: 2000 , stepsize equal to 2−10 times epoch
  • step_size_down (int) – Number of training iterations in the decreasing half of a cycle. If step_size_down is None, it is set to step_size_up. Default: None
  • cycle_momentum (bool) – If True, momentum is cycled inversely to learning rate between ‘base_momentum’ and ‘max_momentum’. Default: True
  • base_momentum (float or list) – Lower momentum boundaries Default: 0.8
  • max_momentum (float or list) – Upper momentum boundaries Default: 0.9
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
>>> scheduler = torch.optim.lr_scheduler.CyclicLR(optimizer, base_lr=0.0001, max_lr=0.01，step_size_up=2000，step_size_down=None,cycle_momentum=True,base_momentum=0.8,max_momentum=0.9)
>>> data_loader = torch.utils.data.DataLoader(...)
>>> for epoch in range(10):
>>>     for batch in data_loader:
>>>         train_batch(...)
>>>         scheduler.step()

OneCycleLR

https://arxiv.org/pdf/1708.07120.pdf

  • max_lr: upper boundary
  • total_steps (int) – The total number of steps in the cycle. Note that if a value is not provided here, then it must be inferred by providing a value for epochs and steps_per_epoch. Default: None
  • pct_start (float) – The percentage of the cycle (in number of steps) spent increasing the learning rate. Default: 0.3
  • cycle_momentum (bool) – If True, momentum is cycled inversely to learning rate between ‘base_momentum’ and ‘max_momentum’. Default: True
  • base_momentum (float or list) – Lower momentum boundaries Default: 0.85
  • max_momentum (float or list) – Upper momentum boundaries Default: 0.95
  • div_factor (float) – Determines the initial learning rate via initial_lr = max_lr/div_factor Default: 25
  • final_div_factor (float) – Determines the minimum learning rate via min_lr = initial_lr/final_div_factor Default: 1e4
>>> data_loader = torch.utils.data.DataLoader(...)
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
>>> scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr=0.01, total_steps = 782*100,pct_start=0.3,cycle_momentum=True,base_momentum=0.85,max_momentum=0.95,div_factor=25,final_div_factor=1e4)
>>> for epoch in range(10):
>>>     for batch in data_loader:
>>>         train_batch(...)
>>>         scheduler.step()

CosineAnnealingWarmRestarts

SGDR
https://arxiv.org/pdf/1608.03983.pdf

  • T_0 (int) – Number of iterations for the first restart.
    第一次循环iters

  • T_mult (int, optional) – A factor increases TiT_{i}Ti​ after a restart. Default: 1.
    每个循环结束后对于循环iters*T_mult，增长循环iters

  • eta_min (float, optional) – Minimum learning rate. Default: 0.

>>> scheduler = CosineAnnealingWarmRestarts(optimizer, T_0=2000, T_mult=1)
>>> iters = len(dataloader)
>>> for epoch in range(20):
>>>     for i, sample in enumerate(dataloader):
>>>         inputs, labels = sample['inputs'], sample['labels']
>>>         optimizer.zero_grad()
>>>         outputs = net(inputs)
>>>         loss = criterion(outputs, labels)
>>>         loss.backward()
>>>         optimizer.step()
>>>         scheduler.step(epoch + i / iters)

Stochastic Weight Averaging

Averaging Weights Leads to Wider Optima and Better Generalization
https://arxiv.org/pdf/1803.05407.pdf

In the example below, swa_model is the SWA model that accumulates the averages of the weights. We train the model for a total of 300 epochs and we switch to the SWA learning rate schedule and start to collect SWA averages of the parameters at epoch 160

>>> loader, optimizer, model, loss_fn = ...
>>> swa_model = torch.optim.swa_utils.AveragedModel(model)
>>> scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=300)
>>> swa_start = 160
>>> swa_scheduler = SWALR(optimizer, swa_lr=0.05)
>>>
>>> for epoch in range(300):
>>>       for input, target in loader:
>>>           optimizer.zero_grad()
>>>           loss_fn(model(input), target).backward()
>>>           optimizer.step()
>>>       if i > swa_start:
>>>           swa_model.update_parameters(model)
>>>           swa_scheduler.step()
>>>       else:
>>>           scheduler.step()
>>>
>>> # Update bn statistics for the swa_model at the end
>>> torch.optim.swa_utils.update_bn(loader, swa_model)
>>> # Use swa_model to make predictions on test data
>>> preds = swa_model(test_input)

def moving_average(net1, net2, alpha=1):
    for param1, param2 in zip(net1.parameters(), net2.parameters()):
        param1.data *= (1.0 - alpha)
        param1.data += param2.data * alpha

总结

分类

纯衰减学习率(FixdLR,ReduceLROnPlateau)
循环学习率(CyclicLR,OneCycleLR)
SWA（Stochastic Weight Averaging）

训练策略需要的超参数超参数的数量详细的训练策略
FixdLR总的iters（epochs）,初始的学习率，衰减系数，步长4从初始学习率开始，每步长次epoch，学习率乘以衰减系数
ReduceLROnPlateau总的iters（epochs），初始的学习率，patience，衰减系数，一个验证集指标，最低学习率6从初始学习率开始根据验证集的指标连续patience不增长（衰减），学习率乘以衰减系数
CyclicLR总的iters（epochs），最高学习率，最低学习率，循环的步长（一般为2-10epoch）4在总的iters内循环步长，每个步长内进行一次学习策略变化
OneCycleLR（Warmup）总的iters（epochs），最高学习率，warmup阶段（一般为0.3），初始学习率（一般为最高学习率/25），最终学习率 (一般为最高学习率/10000)5总的iters先进行warmup提高学习率，再下降学习率
SWA基础学习策略，进行swa的epoch数量，swa的更新率，swa后学习率的衰减epochn+3在基础学习策略后进行swa

FixdLR
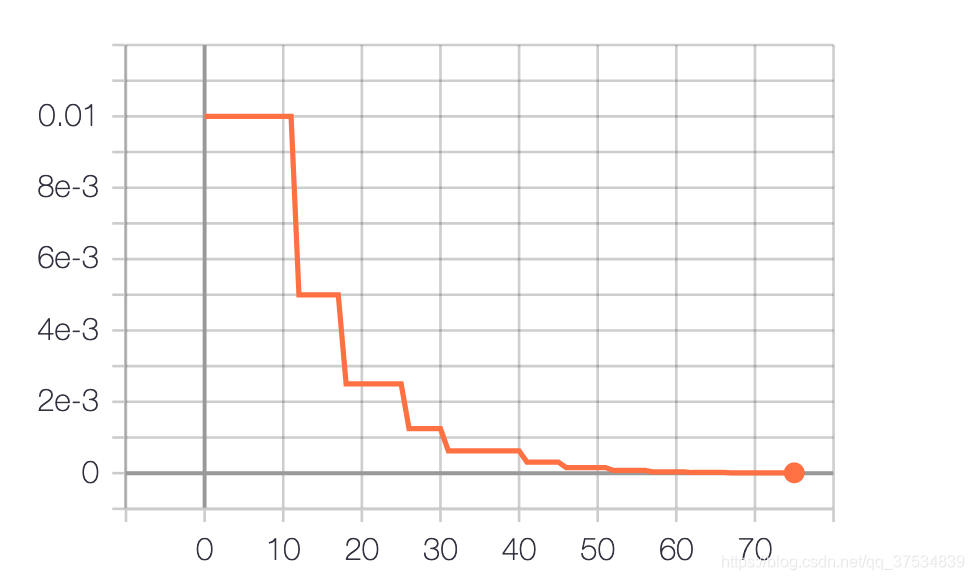
在这里插入图片描述ReduceLROnPlateau
在这里插入图片描述
CyclicLR
在这里插入图片描述

OneCycleLR（Warmup）
在这里插入图片描述
SWA

在这里插入图片描述

实验

实验设置：
基础的学习器：optimizer = optim.SGD(net.parameters(),lr=0.01,momentum=0.9,weight_decay=5e-4)optim.SGD(net.parameters(),lr=0.01,momentum=0.9,weight_decay=5e-4)
数据集：cifer10（训练集50000，测试集10000，10分类）
网络模型：双流efficient_b0的backbone，拼接featuremap，avgpool，fc。
batchsize=64

训练策略具体的超参数设置验证集最高指标run
FixdLR初始学习率0.01，100个epoch，每30个epoch衰减为原先0.1倍86.191
ReduceLROnPlateau初始学习率0.01，100个epoch，每验证集上准确率连续4次不增长，衰减原先0.5倍，最低1e-5avg(85.76,85.16)=85.462
ReduceLROnPlateau初始学习率0.01，100个epoch，每验证集上准确率连续4次不增长，衰减原先0.1倍，最低1e-586.471
OneCycleLR（Warmup）100个epoch，最高学习率0.01，前30个epoch为warmup阶段，初始学习率（一般为最高学习率/25），最终学习率 (一般为最高学习率/10000)avg(86.84,86.84)=86.842
CycleLR(triangle)100个epoch, 最高学习率0.01，最低学习率1e-5，每5.12个epoch进行一次循环，包括2.56个epoch线性从最低学习率到最高和2.56个epoch从最高学习率到最低学习率avg(86.61,86.44)=86.532
CycleLR(cos)100个epoch, 最高学习率0.01，最低学习率1e-5，每6个epoch进行一次循环，包括3个epoch线性从最低学习率到最高和3个epoch从最高学习率到最低学习率86.401
SWA(FixdLR)前80epoch维持0.01学习率，从第80到110epoch从0.01线性衰减到1e-5，最后10epoch维持1e-586.381
SWA(CosineAnnealingLR)前80epoch使用CosineAnnealingLR学习策略，从第80到110epoch从0.01线性衰减到1e-5，最后10epoch维持1e-587.021
SWA(FixdLR)初始学习率0.01，前80epoch使用FixdLR学习策略,每35个epoch衰减为原先0.1，从第80到110epoch从1e-4线性衰减到1e-5，最后10epoch维持1e-585.991

分析

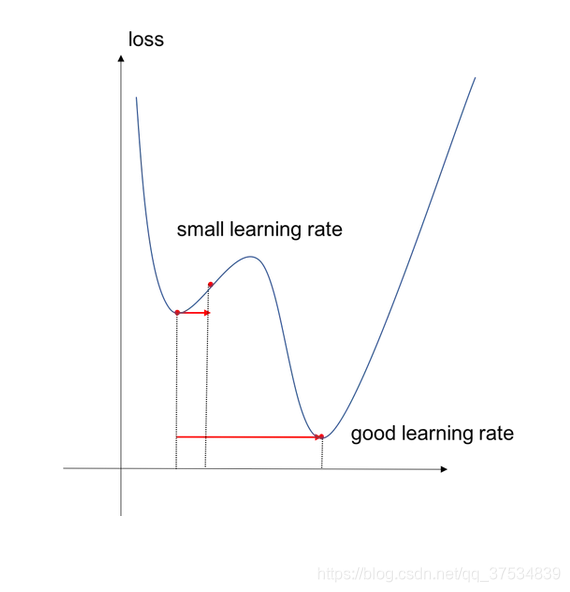
1.CLR的有效的原因？
衰减式的学习策略可能到达一个鞍点并且无法走出，增长的学习率有助于快速走出鞍点。
最佳的学习率在bounds之间，相比于固定的学习率，一个循环的结果更接近最佳的学习率。大学习率与小学习率的trade-off
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
CCA分析*
CCA: 维持仿射变换不变的，快速比较两个网络层representation相似度的一种工具（计算方法）
google brain 2017 NIPS上提出

0->35->65->100：浅层先收敛，深层后收敛
在这里插入图片描述
SGRD，restart从高处到低处，实现，并没有改变浅层的参数，改变的是深层的参数，完成一次倾向于跨越障碍的轨迹。
在这里插入图片描述

对于蒸馏的解释
在这里插入图片描述

2.warm up的有效性原因？
最初在resnet的论文中出现，使用warm up的原因是：初始学习率太大以至于网络无法收敛，因此从小的一个学习率warm up网络。提供全连接层的稳定性。

好的回答：

  • 在训练的开始阶段，模型权重迅速改变mini-batch size较小。

  • 样本方差较大。
    第一种情况很好理解，可以认为，刚开始模型对数据的“分布”理解为零，或者是说“均匀分布”（当然这取决于你的初始化）；在第一轮训练的时候，每个数据点对模型来说都是新的，模型会很快地进行数据分布修正，如果这时候学习率就很大，极有可能导致开始的时候就对该数据“过拟合”，后面要通过多轮训练才能拉回来，浪费时间。当训练了一段时间（比如两轮、三轮）后，模型已经对每个数据点看过几遍了，或者说对当前的batch而言有了一些正确的先验，较大的学习率就不那么容易会使模型学偏，所以可以适当调大学习率。这个过程就可以看做是warmup。那么为什么之后还要decay呢？当模型训到一定阶段后（比如十个epoch），模型的分布就已经比较固定了，或者说能学到的新东西就比较少了。如果还沿用较大的学习率，就会破坏这种稳定性，用我们通常的话说，就是已经接近loss的local optimal了，为了靠近这个point，我们就要慢慢来。第二种情况其实和第一种情况是紧密联系的。在训练的过程中，如果有mini-batch内的数据分布方差特别大，这就会导致模型学习剧烈波动，使其学得的权重很不稳定，这在训练初期最为明显，最后期较为缓解（所以我们要对数据进行scale也是这个道理）。

  • 有助于减缓模型在初始阶段对mini-batch的提前过拟合现象

  • 保持分布的平稳有助于保持模型深层的稳定性

作者：香侬科技
链接：https://www.zhihu.com/question/338066667/answer/771252708
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3.SWA有效的原因？
在这里插入图片描述减少方差，----->在误差可控的范围内，不同模型的差异越大越好。循环余弦策略好于固定策略

4.如何找到一个好的初始学习率？
LR test （网格搜索）
在这里插入图片描述

一切皆是映射：利用深度学习提升个性化营销策略
AI天才研究院
06-22 382
一切皆是映射：利用深度学习提升个性化营销策略 1.背景介绍 在当今数字化时代，个性化营销已经成为企业获取竞争优势的关键手段。传统的营销策略往往依赖于广泛的市场调研和经验判断，然而，这种方法在面对海量数据和复杂的用户行为时显得力不从心。深度学习作为人工智能的一个重要分支，凭借其强大
深度网络学习调研报告
阿黄啦啦
12-10 1万+
深度网络学习调研报告   目  录 1.前言............................................... 3 1.1课题研究的背景及意义.......................... 3 1.2国内外研究的现状.............................. 3 1.3本报告的基本内容.
深度学习调研报告
05-16
神经网络的学习与研究在近十年是一个很热门的研究课题，而最终这些研究成果部分可以体现在我们的日常生活中，神经网络特有的非线性适应性信息处理能力，克服了传统人工智能方法对于直觉的缺陷，使之在神经专家系统、模式识别、智能控制、组合优化、预测等领域得到成功应用。神经网络与其它传统方法相结，将推动人工智能和信息处理技术不断发展。近年来，神经网络在模拟人类的认知的道路上更加深入发展，并与模糊系统、遗传算法、进化机制等结合，形成计算智能，成为人工智能的一个重要方向。虽然神经网络具有这么多的优点与可实用性，但是浅层神经网络在有限样本和计算单元情况下对复杂函数的表示能力有限，针对复杂分类问题其泛化能力受限，已经适应不了高速科技与信息时代的发展所引发的一系列深层次问题，故而引发人们对深层网络的构建、学习与发展
深度学习工具调研
爱无止尽的博客
02-01 511
作者：Vamei 出处：http://www.cnblogs.com/vamei 严禁任何形式转载。   深度学习（Deep Learning）是机器学习的一个进展迅速的分支。Google下围棋的AlphaGo就采用了深度学习算法，从而让机器学习算法广受关注。这里是我对深度学习常用库的一个调研总结。   基于Python的常用方案： Theano + Pylearn2: 大部分基于P
深度学习简单调研
jjhlc的博客
11-23 1775
码隆科技---零售 http://www.malongtech.cn/ 诺亦腾科技---VR Noitom诺亦腾官网 | 动作捕捉及商用虚拟现实整体解决方案 图漾科技---物流、机器人引导、客流检测 图漾科技丨3D相机 – 专注于3D机器视觉的创新科技 速感科技 http://www.qfeeltech.com/page/ 图灵机器人---语音识别 图灵机器人-智能好用的聊天机器人 蓦然认知---多种场景的AI助理 北京蓦然认知科技有限公司 ...
深度学习书籍调研
微电子学与固体电子学-俞驰
02-11 325
注意kaggle的图像比赛其实是pytorch方案居多，如果做图像不要忽略torch。 下面是三个体系,任选其中一种体系即可. --------------Tensorflow体系---------------------------- TensorFlow深度学习 深度学习与TensorFlow实战 TensorFlow实战Google深度学习框架(第2版) 深度学习原理-tensorf...
笔记-深度学习场景调研
ZSY的大后台
06-29 697
深度学习的大潮如火如荼，但深度学习并非所有问题的最好答案。那么哪些方向已经较为成熟应用了深度学习并取得了较好效果呢，通过了解深度学习如何解决不同的问题，从而更深入理解深度学习算法的特点与适用性，做了相关调研，附上链接如下： 深度学习在图像领域的应用，图像分类、图像识别、语义分割、视频检测…这是深度学习最初放光的领域，也是当前研究的最热点，不同类型的网络层出不穷，很少的一部分沉淀下来成为了经典。理...
高中生数学学科“深度学习”的策略研究.pdf
08-18
在探讨高中生数学深度学习策略的研究中，主要目的是通过提高学生的深度学习能力来优化数学教学效果，并为学生数学的可持续发展奠定基础。此研究首先指出高中数学相比初中数学，在难度和深度上有显著提高，而学生课余...
基于省级统一在线平台的深度学习策略.pdf
08-18
3. 深度学习的促进策略：深度学习需要适当的动机情境，高层次的学习者活动，以及与教师和同伴的交互。为此，教育项目如安徽继续教育网络园区管理中心的平台提供了丰富的在线学习支持服务，促进了深度学习的发生。 4...
基于深度学习的小波转化的数字水印去除算法
05-28
【标题】"基于深度学习的小波转化的数字水印去除算法"主要涉及到现代信息技术中的数字图像处理、水印技术和深度学习应用。数字水印是一种在数字媒体中嵌入隐藏信息的技术，通常用于版权保护和防伪。而深度学习是人工...
网络学习空间中大学生深度学习现状与提升策略——基于对H大学教育技术学专业学生的调研.pdf
08-19
此外，调研还显示性别和户籍对深度学习的影响并不显著，而信息素养的水平与深度学习的程度呈现正相关。也就是说，信息素养较高的学生更倾向于进行深度学习。 为了提升大学生在网络学习空间中的深度学习能力，高校...
深度学习-策略学习
perfect_god的博客
07-30 514
J（θ）表示以S为随机变量对V函数进行期望，得到只和θ有关的平均状态价值函数，也就是可以利用J（θ）得到以θ为随机变量，与s无关，找到最好的θ参数，得到与s无关时最大的J（θ）。可以把Qπ挪到右边是因为这里假设Qπ与θ无关，而实际其实是有些关联的，所以这里不太严谨，挪到右边是为了让我们学明白点，好理解点。第二种在连续的时候用，但是由于做积分不太可能，因为近似出的π函数太复杂了，所以用蒙特卡洛近似近似出该积分。如果a离散，则可以直接用，但是一般不行，所以一般用蒙特卡洛近似。如何令策略网络越来越好？...
论文笔记 | 基于深度学习的细粒度物体分类综述
热门推荐
kangdk 视其所以，观其所由，察其所安。
04-19 1万+
节选整理自：A Survey on Deep Learning-based Fine-grained Object Classification and Semantic Segmentation 细粒度分类综述 细粒度分类：同一类中不同子类物体间的分类。 难点：受视角、背景、遮挡等因素影响较大，类内差异较大、类间差异较小。 基于深度学习的物体分类可以大致分为4类： 使用通用DCN...
【模型压缩方法总览】深度学习调研
云端筑梦师
09-21 1772
模型压缩原因 论文Predicting parameters in deep learning提出，其实在很多深度的神经网络中存在着显著的冗余。仅仅使用很少一部分（5%）权值就足以预测剩余的权值。该论文还提出这些剩下的权值甚至可以直接不用被学习。也就是说，仅仅训练一小部分原来的权值参数就有可能达到和原来网络相近甚至超过原来网络的性能（可以看作一种正则化）。 Krizhevsky在2014年的文章中...
【tips-AI】提高模型训练的Pytorch技巧
qq_39448789的博客
12-06 1810
学习率lr很大程度上影响收敛速度和泛化性能。收敛速度很好理解，对泛化性能的影响却不是很直观。泛化性指模型经过训练后，应用到新数据并做出准确预测的能力。lr影响收敛，即模型训练不恰当(过拟合/欠拟合)，准确率P和召回率R有所下降，影响模型的输出，即模型泛化性能差。话回lr，相比于固定学习率，周期性学习率策略被证明是更有效的训练方式，如fastai中的[one cycle学习率策略](https://sgugger.github.io/the-1cycle-policy.html)。从最小lr变成最大。
常用lr_scheduler总结
leo0308的博客
06-13 7467
学习率网络训练中最重要的超参数之一， 通过学习率可以控制模型训练的速度。 因此， 一个好的学习率设置是非常重要的。 本文主要总结常用的学习率， 以及其用法。
【pytorch 优化器】ReduceLROnPlateau详解
devil_son1234的博客
02-21 1万+
【pytorch 优化器】ReduceLROnPlateau详解
关于yolov7的遗传算法进化训练
い天然呆的博客
07-16 1748
据网上消息YOLOv7相同体量下比YOLOv5精度更高，速度快120%(FPS)，比YOLOX快180%(FPS)，比Dual-Swin-T快1200%(FPS)，比ConvNext快550%(FPS)，比SWIN-L快500%(FPS)。最近yolov7刚出来，打算试一波，测测速度以及精度，经过对部分代码的研读，发现大部分还是延续了yolov5的风格，加之yolov6的部分内容以及一些才开源的sota的算法。所有的训练方式以及测试方式和配置文件大体都跟yolov5类似。修改完之后就可以进行遗传进化了。..
torch.optim.lr_scheduler.OneCycleLR
最新发布
m0_49133355的博客
07-17 791
torch.optim.lr_scheduler.OneCycleLR 是 PyTorch 中的一个学习率调度器，它根据 “1cycle” 策略在训练期间调整学习率，可以提高训练性能和收敛性。在这里，它设置为 0.4，表示学习率将在前 40% 的训练步骤中增加，后 60% 的训练步骤中减少。在这种情况下，它设置为 init_lr*10，其中 init_lr 是提供给优化器的初始学习率。在这里，它设置为 10。这个学习率调度器将在训练过程中根据指定的参数动态调整学习率和动量，从而帮助模型更好地收敛。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值