视觉SLAM理论到实践系列
视觉SLAM理论到实践系列(二)——三维物体的刚体运动(1)
视觉SLAM理论到实践系列(二)——三维物体的刚体运动(2)
下面是《视觉SLAM十四讲》学习笔记的系列记录的总链接,本人发表这个系列的文章链接均收录于此
视觉SLAM理论到实践系列文章链接
文章目录
前言
高翔博士的《视觉SLAM14讲》学习笔记的系列记录
视觉SLAM理论到实践系列(二)——三维物体的刚体运动(1)
点与坐标系
2D的情况:用两个坐标加旋转角表达
3D 的情况?
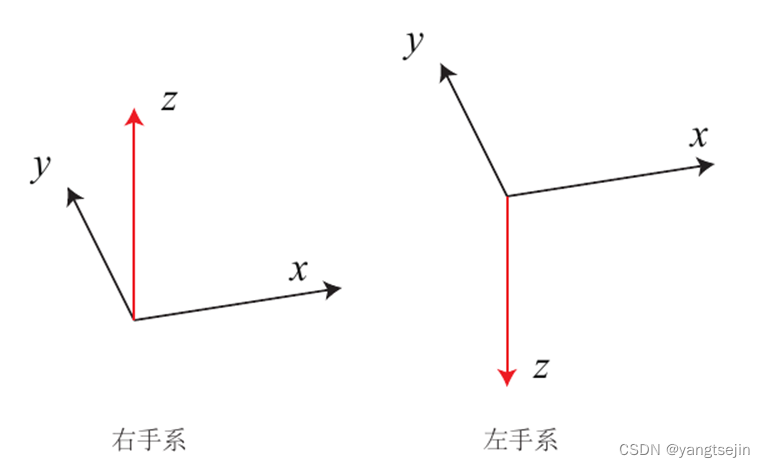
-
向量的运算可由坐标运算表达
-
加法和减法
-
内积
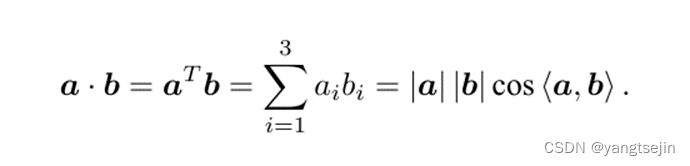
-
外积
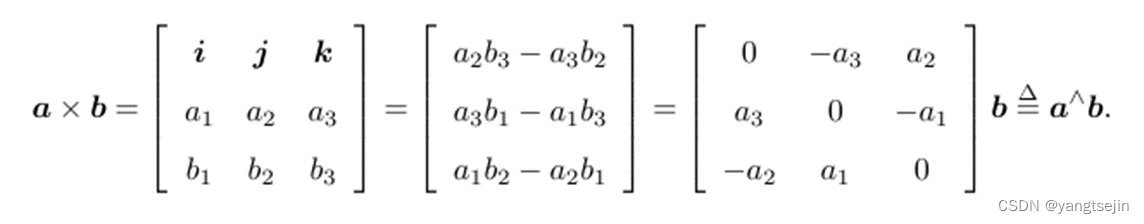
注意
这样就把
a
×
b
a \times b
a×b写成了矩阵与向量的乘法
a
∧
b
a^{\wedge}b
a∧b,把它变成了线性运算。这个符号将在后文经常用到,请记住它,
并且此符号是一个一一映射,意味着任意向量都对应着唯一的一个反对称矩阵,反之亦然:
a
∧
=
[
0
−
a
3
a
2
a
3
0
−
a
1
−
a
2
a
1
0
]
,
a^{\wedge}= \begin{bmatrix} 0&-a_3&a_2\\ a_3&0&-a_1\\ -a_2&a_1&0 \end{bmatrix},
a∧=
0a3−a2−a30a1a2−a10
,
这个符号本质上是叉乘
反对称矩阵的性质
参考:
1.反对称矩阵的基本性质
[
a
]
∧
=
−
[
a
]
∧
T
[\boldsymbol{a}]^{\wedge}=-[\boldsymbol{a}]^{\wedge T}
[a]∧=−[a]∧T
2.叉乘的基本性质,叉乘顺序互换,叉乘结果大小不变,方向相反
[
a
]
∧
b
=
−
[
b
]
∧
a
[\boldsymbol{a}]^{\wedge}\boldsymbol{b}=-[\boldsymbol{b}]^{\wedge}\boldsymbol{a}
[a]∧b=−[b]∧a
3.叉乘的基本性质,向量与自己叉乘等于零向量
[
a
]
∧
a
=
0
[a]^{\wedge}a=0
[a]∧a=0
4.叉乘的基本性质,向量叉乘的结果同时垂直于叉乘的两个向量
b
T
[
a
]
∧
b
=
0
b^T[a]^\wedge\boldsymbol{b}=0
bT[a]∧b=0
5.混合积公式,标量三重积,
a
⋅
(
b
×
c
)
=
b
⋅
(
c
×
a
)
=
c
⋅
(
a
×
b
)
a
T
[
b
]
∧
c
=
b
T
[
c
]
∧
a
=
c
T
[
a
]
∧
b
\begin{aligned}&\boldsymbol{a}\cdot(\boldsymbol{b}\times\boldsymbol{c})=\boldsymbol{b}\cdot(\boldsymbol{c}\times\boldsymbol{a})=\boldsymbol{c}\cdot(\boldsymbol{a}\times\boldsymbol{b})\\\\ &\boldsymbol{a}^T[\boldsymbol{b}]^\wedge\boldsymbol{c}=\boldsymbol{b}^T[\boldsymbol{c}]^\wedge\boldsymbol{a}=\boldsymbol{c}^T[\boldsymbol{a}]^\wedge\boldsymbol{b}\end{aligned}
a⋅(b×c)=b⋅(c×a)=c⋅(a×b)aT[b]∧c=bT[c]∧a=cT[a]∧b
6.向量三重积,
a
×
(
b
×
c
)
=
b
(
a
⋅
c
)
−
c
(
a
⋅
b
)
a\times(b\times c)=b(a\cdot c)-c(a\cdot b)
a×(b×c)=b(a⋅c)−c(a⋅b)
写成矩阵相乘形式有
[
a
]
∧
[
b
]
∧
c
=
b
(
a
T
c
)
−
(
a
T
b
)
c
=
(
b
a
T
)
c
−
(
a
T
b
)
c
=
(
b
a
T
−
a
T
b
I
3
)
c
[\boldsymbol{a}]^\wedge[\boldsymbol{b}]^\wedge\boldsymbol{c}=\boldsymbol{b}\left(\boldsymbol{a}^T\boldsymbol{c}\right)-\left(\boldsymbol{a}^T\boldsymbol{b}\right)\boldsymbol{c}=\left(\boldsymbol{b}\boldsymbol{a}^T\right)\boldsymbol{c}-\left(\boldsymbol{a}^T\boldsymbol{b}\right)\boldsymbol{c}=\left(\boldsymbol{b}\boldsymbol{a}^T-\boldsymbol{a}^T\boldsymbol{b}I_3\right)\boldsymbol{c}
[a]∧[b]∧c=b(aTc)−(aTb)c=(baT)c−(aTb)c=(baT−aTbI3)c
由于对于任意的三维向量
c
c
c 都成立,所以有
[
a
]
∧
[
b
]
∧
=
b
a
T
−
a
T
b
I
3
[\boldsymbol{a}]^{\wedge}[\boldsymbol{b}]^{\wedge}=\boldsymbol{b}\boldsymbol{a}^{T}-\boldsymbol{a}^{T}\boldsymbol{b}I_{3}
[a]∧[b]∧=baT−aTbI3
7.二次幂公式,性质6的一个特例
[
a
]
∧
[
a
]
∧
=
a
a
T
−
a
T
a
I
3
⇒
[
a
]
∧
2
=
a
a
T
−
∥
a
∥
2
2
I
3
[\boldsymbol{a}]^{\wedge}[\boldsymbol{a}]^{\wedge}=\boldsymbol{a}\boldsymbol{a}^T-\boldsymbol{a}^T\boldsymbol{a}I_3\Rightarrow[\boldsymbol{a}]^{\wedge^2}=\boldsymbol{a}\boldsymbol{a}^T-\|\boldsymbol{a}\|_2^2I_3
[a]∧[a]∧=aaT−aTaI3⇒[a]∧2=aaT−∥a∥22I3
8.三次幂公式和特征值,在性质7上两边各左乘一个
[
a
]
∧
[\boldsymbol{a}]^{\wedge}
[a]∧,可以得到
[
a
]
∧
[\boldsymbol{a}]^{\wedge}
[a]∧ 的零化多项式。
[
a
]
∧
3
=
−
∥
a
∥
2
2
[
a
]
∧
λ
3
+
∥
a
∥
2
2
λ
=
0
\begin{aligned}&[\boldsymbol{a}]^{\wedge^3}=-\|\boldsymbol{a}\|_2^2[\boldsymbol{a}]^{\wedge}\\\\ &\lambda^3+\|\boldsymbol{a}\|_2^2\lambda=0\end{aligned}
[a]∧3=−∥a∥22[a]∧λ3+∥a∥22λ=0
因此可以得到
[
a
]
∧
[\boldsymbol{a}]^{\wedge}
[a]∧ 的特征值为
λ
1
=
0
\lambda_1=0
λ1=0,以及
λ
2
、
3
=
i
∥
a
∥
2
\lambda_{2、3}=i\|a\|^2
λ2、3=i∥a∥2,反对称矩阵的特征值有一个是0,另外两个是相等的虚数。特征值0对应的特征向量为
a
\boldsymbol{a}
a,因为有
[
a
]
∧
a
=
0
a
[\boldsymbol{a}]^{\wedge}\boldsymbol{a}=\boldsymbol{0}\boldsymbol{a}
[a]∧a=0a
如果 ∥ a ∥ = 1 \|\boldsymbol{a}\|=1 ∥a∥=1,则有
[ a ] ∧ [ a ] ∧ = a a T − I [ a ] ∧ 3 = − [ a ] ∧ [\boldsymbol{a}]^{\wedge}[\boldsymbol{a}]^{\wedge}=\boldsymbol{a}\boldsymbol{a}^T-I \\ [\boldsymbol{a}]^{\wedge^3}=-[\boldsymbol{a}]^{\wedge} [a]∧[a]∧=aaT−I[a]∧3=−[a]∧
9.当a不为零向量时
R
a
n
k
(
[
a
]
∧
)
=
2
Rank([\boldsymbol{a}]^\wedge)=2
Rank([a]∧)=2
10.零空间
由性质3、性质8和性质9可知,
R
a
n
k
(
[
a
]
∧
)
=
2
Rank([\boldsymbol{a}]^\wedge)=2
Rank([a]∧)=2,
[
a
]
∧
[\boldsymbol{a}]^{\wedge}
[a]∧必有一维零空间,且
a
\boldsymbol{a}
a 是其中一个解,于是
N
u
l
l
(
[
a
]
∧
)
=
S
p
a
n
(
a
)
Null\left([\boldsymbol{a}]^{\wedge}\right)=Span\left(\boldsymbol{a}\right)
Null([a]∧)=Span(a)
11.旋转矩阵的伴随性质,当
U
U
U 是一个旋转矩阵,有
[
U
a
]
∧
=
U
[
a
]
∧
U
T
[\boldsymbol{Ua}]^{\wedge}=\boldsymbol{U}[\boldsymbol{a}]^{\wedge}\boldsymbol{U}^{T}
[Ua]∧=U[a]∧UT
12.三阶反对称矩阵可以分解为
S
=
[
a
]
∧
=
k
U
Z
U
T
S=[\boldsymbol{a}]^{\wedge}=k\boldsymbol{UZ}\boldsymbol{U}^{T}
S=[a]∧=kUZUT
S
S
S 为反对称矩阵,
k
k
k 为常数,
U
U
U 为正交矩阵,
Z
=
[
0
1
0
−
1
0
0
0
0
0
]
\left.Z=\left[\begin{array}{ccc}0&1&0\\-1&0&0\\0&0&0\end{array}\right.\right]
Z=
0−10100000
旋转矩阵
考虑一次旋转
-
坐标系 ( e 1 , e 2 , e 3 ) (e_1,e_2,e_3) (e1,e2,e3) 发生了旋转,变成 ( e 1 ′ , e 2 ′ , e 3 ′ ) (e_1^{'},e_2^{'},e_3^{'}) (e1′,e2′,e3′)
-
向量 a a a 不动,那么它的坐标如何变化?
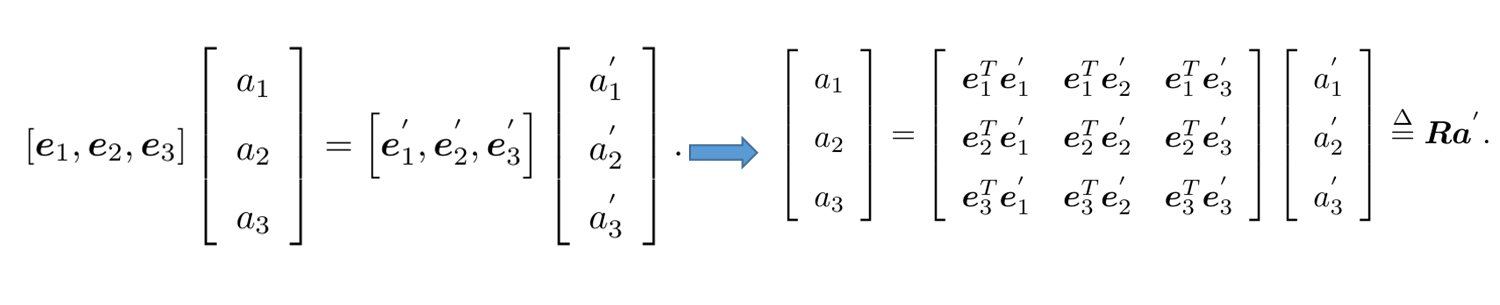
R 称为旋转矩阵
可以验证:
- R是一个正交矩阵;
- R的行列式为+1。
满足这两个性质的矩阵称为旋转矩阵
S
O
(
n
)
=
{
R
∈
R
n
×
n
∣
R
R
T
=
I
,
det
(
R
)
=
1
}
SO(n)=\{\boldsymbol{R}\in\mathbb{R}^{n\times n}|\boldsymbol{RR}^T=\boldsymbol{I},\det(\boldsymbol{R})=1\}
SO(n)={R∈Rn×n∣RRT=I,det(R)=1}
S
O
(
n
)
SO(n)
SO(n) 是Special Orthogonal Group 特殊正交群
这个集合由维空间的旋转矩阵组成,特别地, S O ( 3 ) SO(3) SO(3) 就是指三维空间的旋转。通过旋转矩阵,我们可以直接谈论两个坐标系之间的旋转变换,而不用再从基开始谈起。
注意
[
a
1
a
2
a
3
]
=
[
e
1
T
e
1
′
e
1
T
e
2
′
e
1
T
e
3
′
e
2
T
e
1
′
e
2
T
e
2
′
e
2
T
e
3
′
e
3
T
e
1
′
e
3
T
e
2
′
e
3
T
e
3
′
]
[
a
1
′
a
2
′
a
3
′
]
≜
R
a
′
\left[\begin{array}{c}a_1\\ a_2\\ a_3\end{array}\right]=\left[\begin{array}{ccc}e_1^T e_1^{'}&e_1^T e_2^{'}&e_1^T e_3^{'}\\ e_2^T e_1^{'}&e_2^T e_2^{'}&e_2^T e_3^{'}\\ e_3^T e_1^{'}&e_3^T e_2^{'}&e_3^T e_3^{'}\end{array}\right]\left[\begin{array}{c}a_1^{'}\\ a_2^{'}\\ a_3^{'}\end{array}\right]\triangleq\boldsymbol{Ra^{'}}
a1a2a3
=
e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′
a1′a2′a3′
≜Ra′
于是,2到1的旋可表达为:
a
1
=
R
12
a
2
a_1=R_{12}a_2
a1=R12a2
反之:
a
2
=
R
21
a
1
a_2=R_{21}a_1
a2=R21a1
矩阵关系:
R
21
=
R
12
−
1
=
R
12
T
R_{21}=R_{12}^{-1}=R_{12}^T
R21=R12−1=R12T
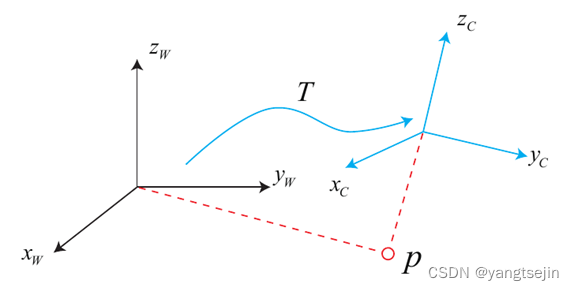
旋转加平移
a
′
=
R
a
+
t
a^{'}=Ra+t
a′=Ra+t
其中,
t
t
t 称为平移向量。相比于旋转,平移部分只需把平移向量加到旋转之后的坐标上,非常简单。通过上式,我们用一个旋转矩阵R和一个平移向量t完整地描述了一个欧氏空间的坐标变换关系。实际当中,我们会定义坐标系1、坐标系2,那么向量a在两个坐标系下的坐标为
a
1
,
a
2
a1,a2
a1,a2 ,它们之间的关系应该是:
a
1
=
R
12
a
2
+
t
12
\boldsymbol{a}_1=R_{12}\boldsymbol{a}_2+t_{12}
a1=R12a2+t12
这里的 R 12 R_{12} R12是指 把坐标系2的向量变换到坐标系1 中。由于向量乘在这个矩阵的右边,它的下标是 从右读到左 的。这也是SLAM 14讲中的习惯写法。
坐标变换很容易搞混,特别是存在多个坐标系的情况下。同理,如果我们要表达“从1到2的旋转矩阵”时,就写成 R 21 R_{21} R21。
关于平移
t
12
t_{12}
t12,它实际对应的是坐标系1原点指向坐标系2原点的向量,在坐标系1下取的坐标,所以建议读者把它记作“从1到2的向量”。但是反过来的
t
21
t_{21}
t21,即从2指向1的向
量在坐标系2下的坐标,却并不等于
−
t
12
-t_{12}
−t12,而是和两个系的旋转还有关系1。所以,当初学者问“我的坐标在哪里”这样的问题时,我们需要清楚地说明这句话的含义。这里“我的坐标”实际上指从世界坐标系指向自己坐标系原点的向量,在世界坐标系下取到的坐标。对应到数学符号上,应该是
t
W
C
t_{WC}
tWC 的取值。同理,它也不是
t
C
W
t_{CW}
tCW。
- 两个坐标系间的运动可用R,t完全描述
- 欧拉定理(Euler’s rotation theorem):刚体在三维空间里的一般运动,可分解为刚体上方某一点的平移,以及绕经过此点的旋转轴的转动。
旋转矩阵左右乘的意义
参考:
可能大家都听到过,左乘旋转矩阵绕固定坐标系旋转,右乘旋转矩阵绕自身坐标系旋转。
单纯记这句话很容易让人产生误解!
首先,这里的左右乘指的并不是某一向量左乘或者右乘旋转矩阵,而是多个旋转矩阵的组合方式是左乘还是右乘。
其次,这句话还遗漏了一个相当重要的信息,绕固定坐标系旋转讨论的是向量的旋转,绕自身坐标系旋转讨论的是坐标变换!这是完全不一样的两种功能,例如我想研究向量的旋转,我可以也只可以将其视为向量绕固定坐标系的旋转。往下看。
1.旋转矩阵左乘
我想要一个向量 p 0 p_0 p0 先绕 x x x 轴转 α \alpha α 度,再绕 y y y 轴转 β \beta β 度,最后绕 z z z 轴转 γ \gamma γ 度,求旋转后向量的位置。
可见这是一个旋转矩阵组合的问题,之前讨论过,向量绕某一坐标轴旋转在数学上展现为向量左乘旋转矩阵,我们按照题意,
当然是先让它绕
x
x
x轴旋转:
p
1
→
=
M
x
(
α
)
×
p
0
→
\overrightarrow{p_1}=M_x(\alpha){\times}\overrightarrow{p_0}
p1=Mx(α)×p0
再绕
y
y
y 轴旋转:
p
2
→
=
M
y
(
β
)
×
p
1
→
\overrightarrow{p_{2}}=M_{y}(\beta)\times\overrightarrow{p_{1}}
p2=My(β)×p1
再绕
z
z
z 轴旋转,那么
p
3
p_3
p3 即为所求向量:
p
3
→
=
M
z
(
γ
)
×
p
2
→
\overrightarrow{p_{3}}=M_{z}(\gamma)\times\overrightarrow{p_{2}}
p3=Mz(γ)×p2
连起来就是:
p
3
→
=
M
z
(
γ
)
×
M
y
(
β
)
×
M
x
(
α
)
×
p
0
→
\overrightarrow{p_3}=M_z(\gamma)\times M_y(\beta)\times M_x(\alpha)\times\overrightarrow{p_0}
p3=Mz(γ)×My(β)×Mx(α)×p0
总的旋转矩阵
R
=
M
z
(
γ
)
×
M
y
(
β
)
×
M
x
(
α
)
R=M_z(\gamma)\times M_y(\beta)\times M_x(\alpha)
R=Mz(γ)×My(β)×Mx(α)
重点来了,让向量 p 0 p0 p0 先后绕 x x x、 y y y、 z z z 轴旋转,其总的旋转矩 R R R 为绕 x x x 轴旋转的矩阵左乘绕 y y y 轴旋转的矩阵再左乘绕 z z z 轴旋转的矩阵。
由此才引入的那句话,左乘绕固定坐标系旋转,现在我们来改一下,应该这么说 :讨论向量旋转问题时,认为向量绕固定坐标轴旋转,旋转矩阵按旋转次序依次左乘,得到最终的旋转矩阵R。
2.旋转矩阵右乘
右乘讨论的就是坐标变换了,来看问题:已知在 C C C 坐标系下表示的向量 p C p_C pC,我想求 p C p_C pC 在原始坐标系0下的表示 p 0 p_0 p0,已知 C C C 坐标系由原始坐标系0绕轴 X 0 X_0 X0 旋转 α \alpha α 度成为坐标系 A A A,再绕轴 Y A Y_A YA旋转成为坐标系 B B B,再绕轴 Z B Z_B ZB旋转成为坐标系 C C C。

再复习一遍, p p p 点在 B B B 坐标系下的坐标,乘以旋转矩阵,得到的是在 A A A 坐标系下的坐标,而 B B B 坐标系是由 A A A 坐标系转了 α \alpha α 角转过去的,可以发现,这是一种“退回”效果,也就是 p p p 点在旋转后的坐标系下的坐标左乘旋转矩阵后,会变为旋转前坐标系下的坐标,这种效果表明旋转后的坐标系一定是绕旋转前坐标系的某一轴转过去的,对于旋转前的坐标系,可以理解为绕自身坐标系的坐标轴旋转后成了旋转后的坐标系。
换句话说,因为你退回来得到的是前坐标系下的坐标,你转过去也必须是绕前坐标系中的坐标轴转过去的,故我们称之为绕自身坐标系旋转(感觉绕的话就多读两遍)这里一定要懂。
再回过来看,咱不是已知 p C p_C pC 求 p 0 p_0 p0 吗,那咱们就一步一步往回退,退到坐标系0为止: 首先由坐标系 C C C 退回到坐标系 B B B,(应该说 p p p 向量在 C C C 系中的表示变换为在 B B B 系中的表示) :
p
B
→
=
M
Z
(
γ
)
×
p
C
→
\overrightarrow{p_{B}}=M_{Z}(\gamma)\times\overrightarrow{p_{C}}
pB=MZ(γ)×pC
再由坐标系
B
B
B 退回到坐标系
A
A
A:
p
A
→
=
M
Y
(
β
)
×
p
B
→
\overrightarrow{p_A}=M_Y(\beta)\times\overrightarrow{p_B}
pA=MY(β)×pB
再由坐标系
A
A
A 退回到坐标系0:
p
0
→
=
M
X
(
α
)
×
p
A
→
\overrightarrow{p_0}=M_X(\alpha){\times}\overrightarrow{p_A}
p0=MX(α)×pA
连起来为:
p
0
→
=
M
X
(
α
)
×
M
Y
(
β
)
×
M
Z
(
γ
)
×
p
C
→
\overrightarrow{p_{0}}=M_{X}(\alpha)\times M_{Y}(\beta)\times M_{Z}(\gamma)\times\overrightarrow{p_{C}}
p0=MX(α)×MY(β)×MZ(γ)×pC
总的旋转矩阵
R
R
R 为:
R
=
M
X
(
α
)
×
M
Y
(
β
)
×
M
Z
(
γ
)
R=M_X(\alpha){\times}M_Y(\beta){\times}M_Z(\gamma)
R=MX(α)×MY(β)×MZ(γ)
之前说过坐标系
C
C
C 是由坐标系0经过绕轴
X
0
X_0
X0 变为坐标系
A
A
A,再绕轴
Y
A
Y_A
YA 变为坐标系
B
B
B,再绕轴
Z
B
Z_B
ZB 旋转才得到的,为了使其退回去,看看旋转矩阵
R
R
R 的写法,是不是绕
x
x
x 轴旋转矩阵右乘
y
y
y 轴旋转旋转右乘
z
z
z 轴旋转矩阵?这就是我们所说的绕自身坐标轴旋转要右乘旋转矩阵。
补充
参考:
二维旋转矩阵
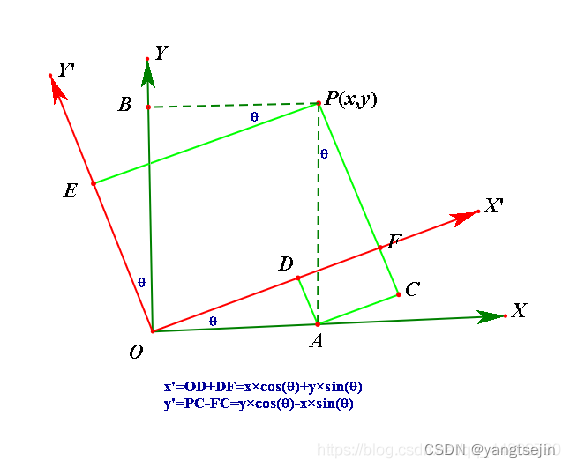
M ( θ ) = [ cos θ − sin θ sin θ cos θ ] = cos θ [ 1 0 0 1 ] + sin θ [ 0 − 1 1 0 ] = exp ( θ [ 0 − 1 1 0 ] ) M(\theta)=\begin{bmatrix}\cos\theta&&-\sin\theta\\\sin\theta&&\cos\theta\end{bmatrix}=\cos\theta\begin{bmatrix}1&&0\\0&&1\end{bmatrix}+\sin\theta\begin{bmatrix}0&&-1\\1&&0\end{bmatrix}=\exp\left(\theta\begin{bmatrix}0&&-1\\1&&0\end{bmatrix}\right) M(θ)=[cosθsinθ−sinθcosθ]=cosθ[1001]+sinθ[01−10]=exp(θ[01−10])
x ′ = cos θ ⋅ x − sin θ ⋅ y y ′ = sin θ ⋅ x + cos θ ⋅ y ⇒ [ x ′ y ′ ] = [ cos θ − sin θ sin θ cos θ ] [ x y ] \begin{gathered} x^{\prime} =\cos\theta\cdot x-\sin\theta\cdot y \\ y^{\prime} =\sin\theta\cdot x+\cos\theta\cdot y \\ \Rightarrow\left[\begin{array}{c}x'\\y'\end{array}\right] =\left[\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right] \end{gathered} x′=cosθ⋅x−sinθ⋅yy′=sinθ⋅x+cosθ⋅y⇒[x′y′]=[cosθsinθ−sinθcosθ][xy]
因此二维坐标系下逆时针旋转矩阵
R
\boldsymbol{R}
R 为:
R
=
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
R=\left[\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right]
R=[cosθsinθ−sinθcosθ]
对于单位矩阵,绕哪个轴旋转,哪一列不用变,然后将二维旋转矩阵替换对应的4个位置,注意,绕Y的旋转矩阵看起来与另外两个不同,它的 − sin β -\sin\beta −sinβ 是在左下
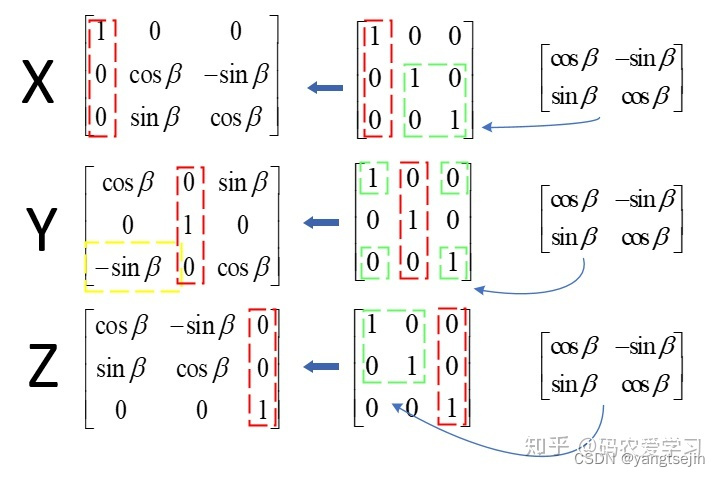
变换矩阵与齐次坐标
旋转加平移在表达复合情况下有不便之处:

这样的形式在变换多次之后会显得很啰嗦。因此,我们引入齐次坐标和变换矩阵
[
a
′
1
]
=
[
R
t
0
T
1
]
[
a
1
]
≜
T
[
a
1
]
{\left[\begin{array}{l}{a^{'}}\\ {1}\\ \end{array}\right]}={\left[\begin{array}{l l}{R}&{t}\\ {0^{T}}&{1}\\ \end{array}\right]}{\left[\begin{array}{l}{a}\\ {1}\\ \end{array}\right]}\triangleq{\boldsymbol{T}}{\left[\begin{array}{l}{a}\\ {1}\\ \end{array}\right]}
[a′1]=[R0Tt1][a1]≜T[a1]
这是一个数学技巧:我们在一个三维向量的末尾添加1,将其变成了四维向量,称为齐次坐标(Homogeneous)。对于这个四维向量,我们可以把旋转和平移写在一个矩阵里,使得整个关系变成线性关系。该式中,矩阵T称为变换矩阵(Transform Matrix)
我们暂时用
a
~
\tilde{a}
a~ 表示
a
a
a 的齐次坐标,即
a
~
=
[
a
1
]
\tilde{a}=\left[\begin{array}{l}{a}\\ {1}\\ \end{array}\right]
a~=[a1]
乘任意非零常数时仍表达同一坐标
a ~ = [ a 1 ] = k [ a 1 ] \tilde{a}= \left[\begin{matrix}a\\1 \end{matrix} \right]= k \left[ \begin{matrix} a\\ 1 \end{matrix} \right] a~=[a1]=k[a1]
那么依靠齐次坐标和变换矩阵,两次变换的叠加就可以有很好的形式:
b
~
=
T
1
a
~
,
c
~
=
T
2
b
~
⇒
c
~
=
T
2
T
1
a
~
\tilde{b}=T_1\tilde{a}, \tilde{c}=T_2\tilde{b}\quad \Rightarrow \quad \tilde{c}=T_2T_1\tilde{a}
b~=T1a~,c~=T2b~⇒c~=T2T1a~
关于变换矩阵T,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左下角为0向量,右下角为1。这种矩阵的集合又称为特殊欧氏群(Special Euclidean Group):
SE
(
3
)
=
{
T
=
[
R
t
0
T
1
]
∈
R
4
×
4
∣
R
∈
SO
(
3
)
,
t
∈
R
3
}
.
\operatorname{SE}(3)=\left\{\boldsymbol{T}=\begin{bmatrix}R&t\\ 0^T&1\end{bmatrix}\in\mathbb{R}^{4\times4}|R\in\operatorname{SO}(3),t\in\mathbb{R}^3\right\}.
SE(3)={T=[R0Tt1]∈R4×4∣R∈SO(3),t∈R3}.
与
S
O
(
3
)
SO(3)
SO(3) 一样,求解该矩阵的逆表示一个反向的变换:
T
−
1
=
[
R
T
−
R
T
t
0
T
1
]
T^{-1}=\begin{bmatrix}R^{T}&-R^{T}t\\ 0^{T}&1\end{bmatrix}
T−1=[RT0T−RTt1]
同样,我们用
T
12
T_{12}
T12 这样的写法来表示从2到1的变换。并且,为了保持符号的简洁,在不引起歧义的情况下,以后不刻意区别齐次坐标与普通坐标的符号,默认使用的是符合运算法则的那一种。
例如,当我们写 T a Ta Ta 时,使用的是齐次坐标(不然没法计算)。而写 R a Ra Ra 时,使用的是非齐次坐标。如果写在一个等式中,就假设齐次坐标到普通坐标的转换是已经做好了的一因为齐次坐标和非齐次坐标之间的转换事实上非常容易,而在C++程序中你可以使用运算符重载来完成这个功能,保证在程序中看到的运算是统一的。
旋转向量和欧拉角
旋转向量
除了旋转矩阵/变换矩阵之外,还存在其他的表示方式
旋转矩阵 R 有九个元素,但仅有三个自由度
能否以更少的元素表达旋转?
我们重新回到理论部分。有了旋转矩阵来描述旋转,有了变换矩阵描述一个6自由度的三维
刚体运动,是不是已经足够了呢?矩阵表示方式至少有以下两个缺点:
-
S
O
(
3
)
SO(3)
SO(3)的旋转矩阵有9个量,但一次旋转只有3个自由度。因此这种表达方式是冗余的。
同理,变换矩阵用16个量表达了6自由度的变换。那么,是否有更紧凑的表示呢? - 旋转矩阵自身带有约束:它必须是个正交矩阵,且行列式为1。变换矩阵也是如此(指自身带有约束,因为变换矩阵不是正交阵)。当想估计或优化一个旋转矩阵或变换矩阵时,这些约束会使得求解变得更困难。
因此,我们希望有一种方式能够紧凑地描述旋转和平移。例如,用一个三维向量表达旋转,用一个六维向量表达变换,可行吗?事实上,任意旋转都可以用一个旋转轴和一个旋转角来刻画。
于是,我们可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量称为旋转向量(或轴角/角轴,Axis-Angle),只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的变量维数正好是六维。
考虑某个用
R
R
R 表示的旋转。如果用旋转向量来描述,假设旋转轴为一个单位长度的向量
n
n
n,角度为
θ
\theta
θ,那么向量
θ
n
\theta n
θn 也可以描述这个旋转。于是,我们要问,两种表达方式之间有什么联系吗?事实上推导它们的转换关系并不难。从旋转向量到旋转矩阵的转换过程由罗德里格斯公式(Rodrigues’s Formula)表明2:
R
=
cos
θ
I
+
(
1
−
cos
θ
)
n
n
T
+
sin
θ
n
∧
.
R=\cos\theta I+(1-\cos\theta){nn}^\text{T}+\sin\theta{n}^\wedge.
R=cosθI+(1−cosθ)nnT+sinθn∧.
符号
∧
\wedge
∧ 是向量到反对称矩阵的转换符,见 转换符。
反之,我们也可以计算从一个旋转矩阵到旋转向量的转换。对于转角
θ
\theta
θ,取两边的迹,有
t
r
(
R
)
=
cos
θ
t
r
(
I
)
+
(
1
−
cos
θ
)
t
r
(
n
n
T
)
+
sin
θ
t
r
(
n
Λ
)
=
3
cos
θ
+
(
1
−
cos
θ
)
=
1
+
2
cos
θ
\begin{aligned} t r\left(R\right)& =\cos\theta t r\left(I\right)+\left(1-\cos\theta\right)\mathrm{tr}\left(n n^{T}\right)+\sin\theta\mathrm{tr}\left(n^{\Lambda}\right) \\ &=3\cos\theta+\left(1-\cos\theta\right) \\ &=1+2\cos\theta \end{aligned}
tr(R)=cosθtr(I)+(1−cosθ)tr(nnT)+sinθtr(nΛ)=3cosθ+(1−cosθ)=1+2cosθ
因此
θ
=
arccos
tr
(
R
)
−
1
2
.
\theta=\operatorname{arccos}{\frac{\operatorname{tr}(R)-1}{2}}.
θ=arccos2tr(R)−1.
关于转轴,旋转轴上的向量在旋转后不发生改变,说明:
R
n
=
n
Rn=n
Rn=n
因此,转轴是矩阵R特征值1对应的特征向量。求解此方程,再归一化,就得到了旋转轴。
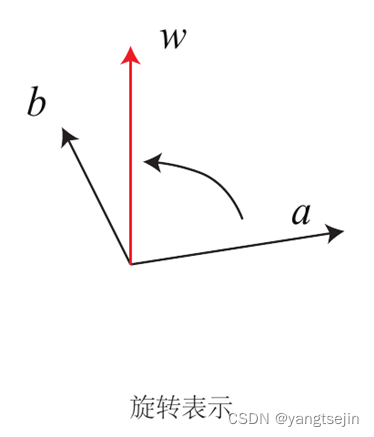
旋转向量
- 方向为旋转轴,长度为转过的角度
- 称为角轴/轴角(Angle Axis)或旋转向量(Rotation Vector)
欧拉角
欧拉角(Euler Angles)
- 将旋转分解为三个方向上的转动
- 例,按Z-Y-X顺序转动
- 轴可以是定轴或动轴,顺序亦可不同
- 常见的有:yaw-pitch-roll,东北天
- 不同领域的习惯有所不同
假设一个刚体的前方(朝向我们的方向)为X轴,右侧为Y轴,上方为Z轴,如下图所示。那么,ZYX转角相当于把任意旋转分解成以下3个轴上的转角:
- 绕物体的Z轴旋转,得到偏航角yaw;
- 绕旋转之后的Y轴旋转,得到俯仰角pitch;
- 绕旋转之后的X轴旋转,得到滚转角roll。
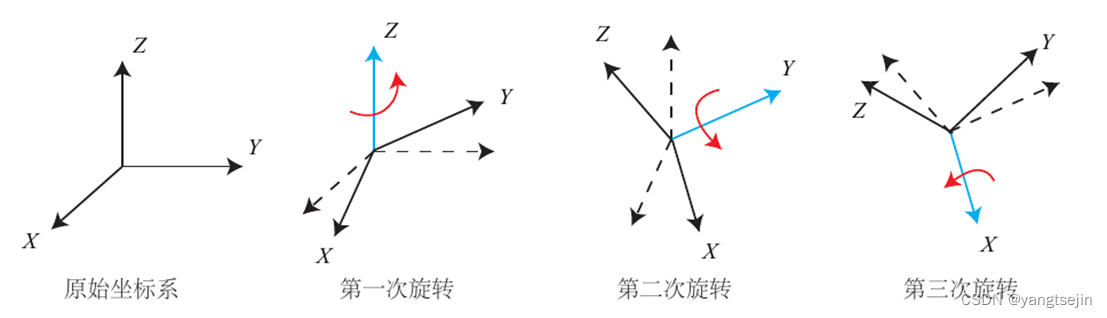
欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock):在俯仰角为±90°时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由3次旋转变成了2次旋转)。这被称为奇异性问题,在其他形式的欧拉角中也同样存在。
理论上可以证明,只要想用3个实数来表达三维旋转,都会不可避免地碰到奇异性问题3。由于这种原理,欧拉角不适用于插值和迭代,往往只用于人机交互中。我们也很少在SLAM程序中直接使用欧拉角表达姿态,同样不会在滤波或优化中使用欧拉角表达旋转(因为它具有奇异性)。
不过,若你想验证自己的算法是否有错,转换成欧拉角能够帮你快速分辨结果是否正确。在某些主体主要为2D运动的场合(例如扫地机、自动驾驶车辆),我们也可以把旋转分解成三个欧拉角,然后把其中一个(例如偏
航角)拿出来作为定位信息输出。
万向锁(Gimbal Lock)
- 欧拉角的奇异性问题
- 在特定值时,旋转自由度减1;
- Yaw-pitch-roll顺序下,当pitch为90度时,存在奇异性
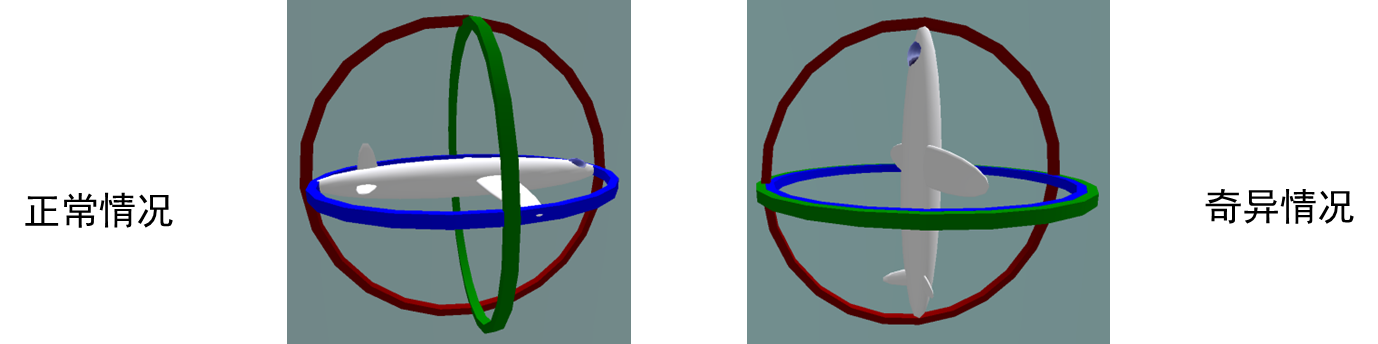
先转的轴会带动后转的轴运动,所以你每次旋转都必须基于初始状态,而不能在一个旋转结果上叠加旋转,否则就会出现被死锁的风险
避免死锁的方法:第二次转动的轴的角度不为90度即可
四元数
参考:
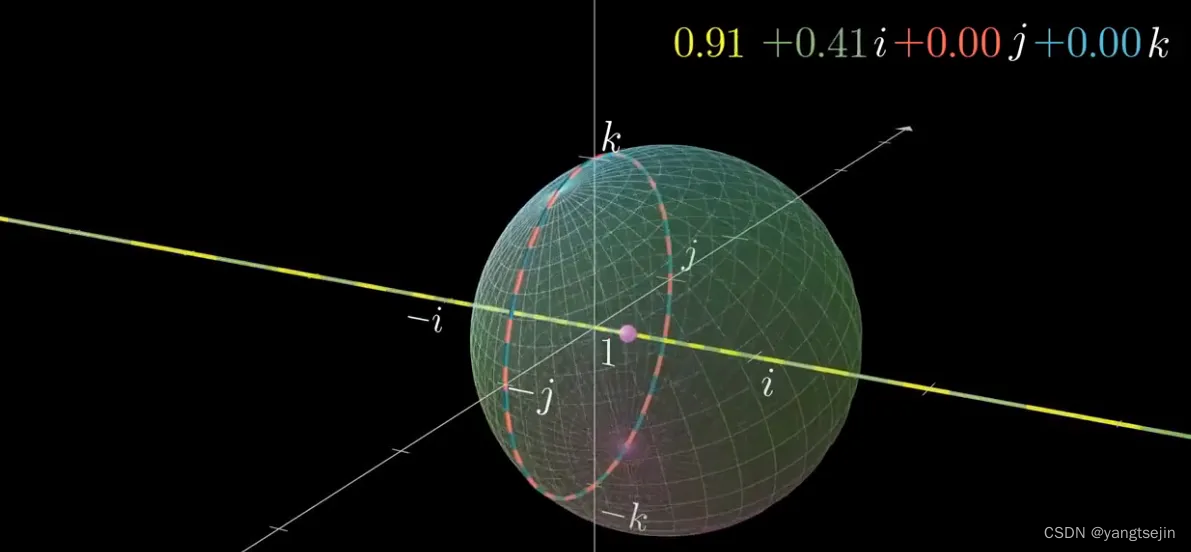
更详细的解释,请看https://eater.net/quaternions
https://github.com/CatOnly/CrashNote/tree/master/LinearAlgebra([LinearAlgebra](books and docs\CrashNotes-master\LinearAlgebra))
四元数定义
旋转矩阵用9个量描述3自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但具有奇异性。
事实上,我们找不到不带奇异性的三维向量描述方式。这有点类似于用两个坐标表示地球表面(如经度和纬度),将必定存在奇异性(纬度为±90°时经度无意义)。
我们用复数集C表示复平面上的向量,而复数的乘法则表示复平面上的旋转:例如,乘上复数i相当于逆时针把一个复向量旋转90°。
类似地,在表达三维空间旋转时,也有一种类似于复数的代数:四元数(Quaternion)。四元数是Hamilton找到的一种扩展的复数。它既是紧凑的,也没有奇异性。如果说缺点,四元数不够直观,其运算稍复杂些。
把四元数与复数类比可以帮助你更快地理解四元数。例如,当我们想要将复平面的向量旋转
θ
\theta
θ 角时,可以给这个复向量乘以
e
i
θ
e^{i\theta}
eiθ。这是极坐标表示的复数,它也可以写成普通的形式,只要使用欧拉公式即可:
e
i
θ
=
cos
θ
+
i
sin
θ
.
\mathrm{e}^{i\theta}=\cos\theta+i\sin\theta.
eiθ=cosθ+isinθ.
这正是一个单位长度的复数。所以,在二维情况下,旋转可以由单位复数来描述。
z
=
x
+
i
y
=
ρ
e
i
θ
z=x+iy=\rho e^{i\theta}
z=x+iy=ρeiθ
乘
i
i
i 即转90度,乘
−
i
-i
−i 转 -90度
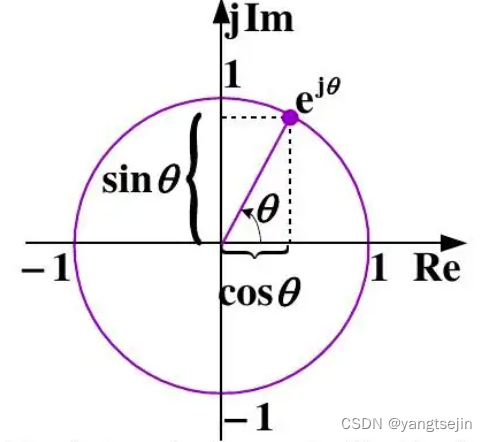
类似地,我们会看到,三维旋转可以由单位四元数来描述。
一个四元数q拥有一个实部和三个虚部
q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
q=q_0+q_1i+q_2j+q_3k
q=q0+q1i+q2j+q3k
其中,
i
,
j
,
k
i,j,k
i,j,k为四元数的三个虚部。这三个虚部满足以下关系式:
{
i
2
=
j
2
=
k
2
=
−
1
j
=
k
,
ji
=
−
k
jk
=
i
,
kj
=
−
i
ki
=
j
,
ik
=
−
j
.
\begin{cases}\text{i}^2=j^2=k^2=-1\\ \text{j}=\text{k},\text{ji}=-\text{k}\\ \text{jk}=\text{i},\text{kj}=-i\\ \text{ki}=j,\text{ik}=-j\end{cases}.
⎩
⎨
⎧i2=j2=k2=−1j=k,ji=−kjk=i,kj=−iki=j,ik=−j.
如果把
i
,
j
,
k
i,j,k
i,j,k 看成三个坐标轴,那么它们与自己的乘法和复数一样,相互之间的乘法和外积一样,即类似于叉乘。
有时,也用一个标量和一个向量来表达四元数:
q
=
[
s
,
v
]
T
,
s
=
q
0
∈
R
,
v
=
[
q
1
,
q
2
,
q
3
]
T
∈
R
3
q=[s,v]^{\mathsf{T}},\quad s=q_0\in\mathbb{R},\quad v=[q_1,q_2,q_3]^{\mathsf{T}}\in\mathbb{R}^3
q=[s,v]T,s=q0∈R,v=[q1,q2,q3]T∈R3
这里,s称为四元数的实部,而v称为它的虚部。如果一个四元数的虚部为0,则称为实四元数;反之,若它的实部为0,则称为虚四元数。
四元数的运算
四元数和通常的复数一样,可以进行一系列的运算。常见的有四则运算、共轭、求逆、数乘等。
现有两个四元数
q
a
,
q
b
q_a,q_b
qa,qb,它们的向量表示为
[
s
a
,
v
a
]
T
,
[
s
b
,
v
b
]
T
[s_a,v_a]^T,[s_b,v_b]^T
[sa,va]T,[sb,vb]T,或者原始四元数表示为
q
a
=
s
a
+
z
a
i
+
y
a
j
+
z
a
k
,
q
b
=
s
b
+
x
0
i
+
y
b
j
+
z
0
k
q_a=s_a+z_a\mathrm{i}+y_a\mathrm{j}+z_a\mathrm{k},\quad q_b=s_b+\mathrm{x_0}\mathrm{i}+y_b\mathrm{j}+z_0\mathrm{k}
qa=sa+zai+yaj+zak,qb=sb+x0i+ybj+z0k
那么,其运算可表示如下。
(1)加法和减法
四元数
q
a
,
q
b
q_a,q_b
qa,qb 的加减运算为
q
a
±
q
b
=
[
s
a
±
s
b
,
v
a
±
v
b
]
T
q_a\pm q_b=\left[s_a\pm s_b,v_a\pm v_b\right]^T
qa±qb=[sa±sb,va±vb]T
(2)乘法
乘法是把
q
a
q_a
qa 的每一项与
q
b
q_b
qb 的每项相乘,最后相加,虚部要按照乘法公式进行。整理可得
q
a
q
b
=
y
a
y
b
−
x
a
x
b
−
y
a
y
b
−
z
a
z
b
+
(
s
a
x
b
+
x
a
s
b
+
y
a
z
b
−
z
a
y
b
)
i
+
(
s
a
y
b
−
x
a
z
b
+
y
a
s
b
+
z
a
x
b
)
j
+
(
s
a
z
b
+
x
a
y
b
−
y
a
x
b
+
z
a
s
b
)
k
\begin{aligned} q_a q_b=& y_{a}y_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b} \\ &+\left(s_a x_b+x_a s_b+y_a z_b-z_a y_b\right)i \\ &+\left(s_{a}y_{b}-x_{a}z_{b}+y_{a}s_{b}+z_{a}x_{b}\right)j \\ &+\left(s_{a}z_{b}+x_{a}y_{b}-y_{a}x_{b}+z_{a}s_{b}\right)k \end{aligned}
qaqb=yayb−xaxb−yayb−zazb+(saxb+xasb+yazb−zayb)i+(sayb−xazb+yasb+zaxb)j+(sazb+xayb−yaxb+zasb)k
虽然稍为复杂,但形式上是整齐有序的。如果写成向量形式并利用内外积运算,该表达会更加简洁:
q
a
q
b
=
[
s
a
s
b
−
v
a
T
v
b
,
s
a
v
b
+
s
b
v
a
+
v
a
×
v
b
]
T
q_{a}q_{b}=\left[s_{a}s_{b}-v_{a}^{\mathrm{T}}v_{b},s_{a}v_{b}+s_{b}v_{a}+v_{a}\times v_{b}\right]^{\mathrm{T}}
qaqb=[sasb−vaTvb,savb+sbva+va×vb]T
在该乘法定义下,两个实四元数乘积仍是实的,这与复数是一致的。然而,我们注意到由于最后一项外积的存在,四元数乘法通常是不可交换的,除非
v
a
v_a
va 和
v
b
v_b
vb 在
R
3
\mathbb{R}^3
R3 中共线,此时外积项为零。
四元数 q 1 q_1 q1 乘以 q 2 q_2 q2 ,会把 q 2 q_2 q2 以 q 1 q_1 q1 的大小放缩,然后再施加一种特殊的四维的旋转

(3)模长
四元数的模长定义为
∥
q
a
∥
=
s
a
2
+
x
a
2
+
y
a
2
+
z
a
2
\|q_a\|=\sqrt{s_a^2+x_a^2+y_a^2+z_a^2}
∥qa∥=sa2+xa2+ya2+za2
可以验证,两个四元数乘积的模即模的乘积。这使得单位四元数相乘后仍是单位四元数。
∥
q
a
q
b
∥
=
∥
q
a
∥
∥
q
b
∥
.
\|q_aq_b\|=\|q_a\|\|q_b\|.
∥qaqb∥=∥qa∥∥qb∥.
(4)共轭
四元数的共轭是把虚部取成相反数:
q
a
∗
=
s
a
−
x
a
i
−
y
k
j
−
z
a
k
=
[
s
k
,
−
ν
a
]
⊤
q_a^*=s_a-x_a i-y_k j-z_a k=[s_k,-\nu_a]^{\top}
qa∗=sa−xai−ykj−zak=[sk,−νa]⊤
四元数共轭与其本身相乘,会得到一个实四元数,其实部为模长的平方:
q
∗
q
=
q
q
∗
=
[
s
a
2
+
v
T
v
,
0
]
⊤
.
q^*q=qq^*=[s_a^2+v^\mathrm{T}v,0]^\top.
q∗q=qq∗=[sa2+vTv,0]⊤.
(5)逆
一个四元数的逆为
q
−
1
=
q
∗
∥
q
∥
2
.
q^{-1}=\frac{q^*}{\|q\|^2.}
q−1=∥q∥2.q∗
按此定义,四元数和自己的逆的乘积为实四元数1:
q
q
−
1
=
q
−
1
q
=
1.
qq^{-1}=q^{-1}q=1.
qq−1=q−1q=1.
如果
q
q
q 为单位四元数,其逆和共轭就是同一个量。同时,乘积的逆具有和矩阵相似的性质:
(
q
a
q
b
)
−
1
=
q
b
−
1
q
a
−
1
.
(q_{a}q_{b})^{-1}=q_{b}^{-1}q_{a}^{-1}.
(qaqb)−1=qb−1qa−1.
(6)数乘
和向量相似,四元数可以与数相乘:
k
q
=
[
k
s
,
k
v
]
T
\mathbf{k}q=[\mathbf{k}s,\mathbf{k}v]^{\mathsf{T}}
kq=[ks,kv]T
四元数到角轴:
q
=
[
cos
θ
2
,
n
x
sin
θ
2
,
n
y
sin
θ
2
,
n
z
sin
θ
2
]
T
q=\left[\cos\frac\theta2,n_x\sin\frac\theta2,n_y\sin\frac\theta2,n_z\sin\frac\theta2\right]^T
q=[cos2θ,nxsin2θ,nysin2θ,nzsin2θ]T
角轴到四元数:
{
θ
=
2
arccos
q
0
[
n
x
,
n
y
,
n
z
]
T
=
[
q
1
,
q
2
,
q
3
]
T
/
sin
θ
2
\begin{cases}\theta=2\arccos q_0\\ \left[n_x,n_y,n_z\right]^T=\left[q_1,q_2,q_3\right]^T/\sin\frac\theta2\end{cases}
{θ=2arccosq0[nx,ny,nz]T=[q1,q2,q3]T/sin2θ
用四元数表示旋转
我们可以用四元数表达对一个点的旋转。假设有一个空间三维点 p = [ x , y , z ] ∈ R 3 p=[x,y,z]∈\mathbb{R}^3 p=[x,y,z]∈R3 ,以及一个由单位四元数 q q q 指定的旋转。三维点 p p p 经过旋转之后变为 p ′ p' p′ 。如果使用矩阵描述,那么有 p ′ = R p p'=Rp p′=Rp 。而如果用四元数描述旋转,它们的关系又如何表达呢?
首先,把三维空间点用一个虚四元数来描述:
p
=
[
0
,
x
,
y
,
z
]
T
=
[
0
,
v
]
T
p=\left[0,x,y,z\right]^{T}=\left[0,v\right]^{T}
p=[0,x,y,z]T=[0,v]T
相当于把四元数的3个虚部与空间中的3个轴相对应。那么,旋转后的点p可表示为这样的乘积:
p
′
=
q
p
q
−
1
p^{\prime}=q p q^{-1}
p′=qpq−1
这里的乘法均为四元数乘法,结果也是四元数。最后把
p
′
p'
p′ 的虚部取出,即得旋转之后点的坐标。
并且,可以验证(留作习题),计算结果的实部为0,故为纯虚四元数。
使用
使用四元数
q
q
q 对点
p
p
p 进行变换,得到四维点
p
′
p'
p′ ,将后三维取出即为坐标
p
′
=
q
p
q
−
1
p^{\prime}=q p q^{-1}
p′=qpq−1
虽然数学实质如上所述,但是Eigen已经将四元数的旋转运算重载,平时只需要这么算就行了
p
′
=
q
∗
p
p'=q*p
p′=q∗p
补充
(1)四元数好用难理解,欧拉角难用好理解
(2)旋转左乘和右乘是有区别的,绝大多数人习惯左乘,不要给自己找事儿
(3)四种变换之间的转换
- 对同一旋转/姿态的不同描述方式是等价的
- 描述之间可以相互转化,但这不是重点
(4)关于位姿与旋转
有时候,我们用这些描述旋转的量来描述一个刚体的姿态,有时候我们又用旋转量来描述刚体在一段时间内的变化,要弄清楚这个很不容易
四元数到其他旋转的表示
任意单位四元数描述了一个旋转,该旋转也可用旋转矩阵或旋转向量描述。现在来考察四元数与旋转向量、旋转矩阵之间的转换关系。在此之前,我们要说,四元数乘法也可以写成一种矩阵的乘法。设 q = [ s , v ] T q=[s,v]^{\mathsf{T}} q=[s,v]T 那么,定义如下的符号 + + + 和 ⊕ ⊕ ⊕ 为
q + = [ s − v T v s I + v ∧ ] , q ⨁ = [ s − v T v s I − v ∧ ] q^+=\begin{bmatrix}s&-v^{\mathrm{T}}\\ v&sI+v^{\wedge}\end{bmatrix}, \quad q^{\bigoplus}=\begin{bmatrix}s&-v^{\mathrm{T}}\\ v&sI-v^{\wedge}\end{bmatrix} q+=[sv−vTsI+v∧],q⨁=[sv−vTsI−v∧]
这两个符号将四元数映射成为一个4×4的矩阵。于是四元数乘法可以写成矩阵的形式:
q 1 + q 2 = [ s 1 − v 1 T v 1 s 1 I + v 1 ∧ ] [ s 2 v 2 ] = [ − v 1 T v 2 + s 1 s 2 s 1 v 2 + s 2 v 1 + v 1 ∧ v 2 ] = q 1 q 2 q_1^+q_2=\begin{bmatrix}s_1&-v_1^T\\v_1&s_1I+v_1^{\wedge}\end{bmatrix}\begin{bmatrix}s_2\\v_2\end{bmatrix} =\begin{bmatrix}-v_1^T v_2+s_1s_2\\s_1v_2+s_2v_1+v_1^{\wedge}v_2\end{bmatrix}=q_1q_2 q1+q2=[s1v1−v1Ts1I+v1∧][s2v2]=[−v1Tv2+s1s2s1v2+s2v1+v1∧v2]=q1q2
同理亦可证:
q 1 q 2 = q 1 + q 2 = q 2 ⨁ q 1 . q_1q_2=q_1^+q_2=q_2^{\bigoplus}q_1. q1q2=q1+q2=q2⨁q1.
然后,考虑使用四元数对空间点进行旋转的问题。根据前面的说法,有
p ′ = q p q − 1 = q + p + q − 1 = q + q − 1 ⨁ p . \begin{aligned} p'&=q p q^{-1}=q^{+}p^{+}q^{-1} \\ &=q^{+}q^{-1^{\bigoplus}}p. \end{aligned} p′=qpq−1=q+p+q−1=q+q−1⨁p.
代入两个符号对应的矩阵,得
q + ( q − 1 ) ⨁ = [ s − v T v s I + v ∧ ] [ s v T − v s I + v ∧ ] = [ s 2 + v T v s v T − s v T + v T v ∧ s v T − s v T − v ∧ v v v T + s 2 I + 2 s v ∧ + ( v ∧ ) 2 ] = [ 1 0 0 T v v T + s 2 I + 2 s v ∧ + ( v ∧ ) 2 ] \begin{aligned} {q}^{+}\left({q}^{-1}\right)^{\bigoplus} &= \begin{bmatrix}s&-v^{T}\\ v&sI+v^{\wedge}\end{bmatrix} \begin{bmatrix} s&v^{T}\\ -v&sI+v^{\wedge} \end{bmatrix} \\ &= \begin{bmatrix} s^2+v^{T}v& sv^{T}-sv^{T}+v^{T}v^{\wedge}\\ sv^{T}-sv^{T}-v^{\wedge}v &v v^{T}+s^2I+2s v^{\wedge}+\left(v^{\wedge}\right)^2 \end{bmatrix} \\ &= \begin{bmatrix} 1&\textbf{0}\\ \textbf{0}^{T}&v v^{T}+s^2I+2s v^{\wedge}+\left(v^{\wedge}\right)^2 \end{bmatrix} \end{aligned} q+(q−1)⨁=[sv−vTsI+v∧][s−vvTsI+v∧]=[s2+vTvsvT−svT−v∧vsvT−svT+vTv∧vvT+s2I+2sv∧+(v∧)2]=[10T0vvT+s2I+2sv∧+(v∧)2]
因为 p p p 和 p ′ p' p′ 都是虚四元数,所以事实上该矩阵的右下角即给出了从四元数到旋转矩阵的变换关系:
R = v v T + s 2 I + 2 s v ∧ + ( v ∧ ) 2 R=v v^{\mathsf{T}}+s^2I+2s v^{\wedge}+\left(v^{\wedge}\right)^2 R=vvT+s2I+2sv∧+(v∧)2
为了得到四元数到旋转向量的转换公式,对上式两侧求迹,得
t r ( R ) = tr ( v v T + 3 s 2 + 2 s ⋅ 0 + tr ( ( v ∧ ) 2 ) = v 1 2 + v 2 2 + v 3 2 + 3 s 2 − 2 ( v 1 2 + v 2 2 + v 3 2 ) = ( 1 − s 2 ) + 3 s 2 − 2 ( 1 − s 2 ) = 4 s 2 − 1. \begin{aligned} t r\left(R\right)& =\operatorname{tr}(v v^{\mathsf{T}}+3s^{2}+2s\cdot0+\operatorname{tr}((v^{\wedge})^{2}) \\ &=v_1^2+v_2^2+v_3^2+3s^2-2(v_1^2+v_2^2+v_3^2) \\ &=(1-s^2)+3s^2-2(1-s^2) \\ &=4s^{2}-1. \end{aligned} tr(R)=tr(vvT+3s2+2s⋅0+tr((v∧)2)=v12+v22+v32+3s2−2(v12+v22+v32)=(1−s2)+3s2−2(1−s2)=4s2−1.
又由式 θ = arccos tr ( R ) − 1 2 \theta=\operatorname{arccos}{\frac{\operatorname{tr}(R)-1}{2}} θ=arccos2tr(R)−1 可得
θ = arccos tr ( R − 1 ) 2 = arccos ( 2 s 2 − 1 ) , \begin{gathered} \theta=\operatorname{arccos}{\frac{\operatorname{tr}(R-1)}{2}} \\ =\arccos(2s^2-1), \end{gathered} θ=arccos2tr(R−1)=arccos(2s2−1),
即
cos θ = 2 s 2 − 1 = 2 cos 2 θ 2 − 1 \cos\theta=2s^2-1=2\cos^2\frac\theta2-1 cosθ=2s2−1=2cos22θ−1
所以:
θ = 2 arccos s \theta=2\operatorname{arccos}s θ=2arccoss
至于旋转轴,如果在式
q + ( q − 1 ) ⨁ = [ s − v T v s I + v ∧ ] [ s v T − v s I + v ∧ ] = [ 1 0 0 τ v v T + s 2 I + 2 s v ∧ + ( v ∧ ) 2 ] \textbf{q}^{+}\left(\textbf{q}^{-1}\right)^{\bigoplus}= \begin{bmatrix}s&-v^{T}\\ v&sI+v^{\wedge}\end{bmatrix} \begin{bmatrix} s&v^{T}\\ -v&sI+v^{\wedge} \end{bmatrix}= \begin{bmatrix} 1&\textbf{0}\\ \textbf{0}^{\tau}&v v^{T}+s^2I+2s v^{\wedge}+\left(v^{\wedge}\right)^2 \end{bmatrix} q+(q−1)⨁=[sv−vTsI+v∧][s−vvTsI+v∧]=[10τ0vvT+s2I+2sv∧+(v∧)2]
中用 q q q 的虚部代替 p p p ,易知 q q q 的虚部组成的向量在旋转时是不动的,即构成旋转轴。于是只要将它除掉它的模长,即得。总而言之,四元数到旋转向量的转换公式如下:
{ θ = 2 arccos q 0 [ n x , n y , n x ] T = [ q 1 , q 2 , q 3 ] T / sin θ 2 \begin{cases}\theta=2\arccos q_0\\ \left[n_x,n_y,n_x\right]^\text{T}=\left[q_1,q_2,q_3\right]^\text{T}/\sin\frac{\theta}{2}\end{cases} {θ=2arccosq0[nx,ny,nx]T=[q1,q2,q3]T/sin2θ
至于如何从其他方式转换到四元数,只须把上述步骤倒过来处理即可。在实际编程中,程序库通常会为我们准备好各种形式之间的转换。无论是四元数、旋转矩阵还是轴角,它们都可以用来描述同一个旋转。我们应该在实际中选择最方便的形式,而不必拘泥于某种特定的形式。
四元数和轴角的关系
假设某个旋转运动的旋转轴为单位向量 $ \boldsymbol{n}$,绕该轴旋转的角度为 $ \theta$,那么它对应的单位四元数为:
q
=
[
cos
θ
2
n
sin
θ
2
]
\boldsymbol{q}=\begin{bmatrix}\cos\frac{\theta}{2}\\ \boldsymbol{n}\sin\frac{\theta}{2}\end{bmatrix}
q=[cos2θnsin2θ]
当旋转一段微小的时间,即旋转角度趋于零时,容易有:
Δ
q
=
[
cos
δ
θ
2
n
sin
δ
θ
2
]
≈
[
1
n
δ
θ
2
]
=
[
1
1
2
δ
θ
]
\Delta\mathbf{q}=\begin{bmatrix}\cos\frac{\delta\theta}{2}\\ \mathbf{n}\sin\frac{\delta\theta}{2}\end{bmatrix}\approx\begin{bmatrix}1\\\mathbf{n}\frac{\delta\theta}{2}\end{bmatrix}=\begin{bmatrix}1\\ \frac{1}{2}\delta\theta\end{bmatrix}
Δq=[cos2δθnsin2δθ]≈[1n2δθ]=[121δθ]
其中
δ
θ
\delta \theta
δθ 的方向表示旋转轴,模长表示旋转角度。
四元数导数
参考:
角速度有:
ω
=
lim
Δ
t
→
0
δ
θ
Δ
t
\boldsymbol{\omega}=\lim_{\Delta t\to0}\frac{\delta\theta}{\Delta t}
ω=Δt→0limΔtδθ
四元数的时间导数为:
q
˙
≜
lim
Δ
t
→
0
q
(
t
+
Δ
t
)
−
q
(
t
)
Δ
t
=
lim
Δ
t
→
0
q
⊗
Δ
q
−
q
Δ
t
=
lim
Δ
t
→
0
q
⊗
(
[
1
1
2
δ
θ
]
−
[
1
0
]
)
Δ
t
=
q
⊗
[
0
1
2
ω
]
\begin{aligned} \mathbf{\dot{q}}& \triangleq\lim_{\Delta t\to0}\frac{\mathbf{q}(t+\Delta t)-\mathbf{q}(t)}{\Delta t} \\ &=\lim_{\Delta t\to0}\frac{\mathbf{q}\otimes\Delta\mathbf{q}-\mathbf{q}}{\Delta t} \\ &=\lim_{\Delta t\to0}\frac{\mathbf{q}\otimes\left(\begin{bmatrix}1\\\frac12\boldsymbol{\delta\theta}\end{bmatrix}-\begin{bmatrix}1\\\mathbf{0}\end{bmatrix}\right)}{\Delta t} \\ &=\mathbf{q}\otimes\begin{bmatrix}0\\\frac12\boldsymbol{\omega}\end{bmatrix} \end{aligned}
q˙≜Δt→0limΔtq(t+Δt)−q(t)=Δt→0limΔtq⊗Δq−q=Δt→0limΔtq⊗([121δθ]−[10])=q⊗[021ω]
或者有
设初始旋转为
q
=
[
s
,
v
]
\text{q}=[s,\mathbf{v}]
q=[s,v],然后,发生了角轴为
ω
,
θ
\omega, \theta
ω,θ 的旋转(右乘,对应四元数记作
Δ
q
\Delta \text{q}
Δq),那么
q
\text{q}
q 相对该旋转的导数为:
lim
θ
→
0
q
⊗
Δ
q
−
q
θ
=
lim
θ
→
0
[
s
cos
θ
2
−
v
T
ω
sin
θ
2
,
s
ω
sin
θ
2
+
cos
θ
2
v
+
v
×
ω
sin
θ
2
]
⊤
−
q
θ
=
lim
θ
→
0
[
s
(
cos
θ
2
−
1
)
−
v
T
ω
sin
θ
2
,
s
ω
sin
θ
2
+
(
cos
θ
2
−
1
)
v
+
v
×
ω
sin
θ
2
]
⊤
θ
=
[
−
1
2
v
T
ω
,
1
2
s
ω
+
1
2
v
×
ω
]
⊤
=
q
⊗
[
0
,
1
2
ω
]
⊤
\begin{aligned} \operatorname*{lim}_{\theta\to0}{\frac{\mathbf{q}\otimes\Delta\mathbf{q}-\mathbf{q}}{\theta}}& =\operatorname*{lim}_{\theta\to0}{\frac{\left[s\cos{\frac{\theta}{2}}-\mathbf{v}^{T}\omega\sin{\frac{\theta}{2}},s\omega\sin{\frac{\theta}{2}}+\cos{\frac{\theta}{2}}\mathbf{v}+\mathbf{v}\times\omega\sin{\frac{\theta}{2}}\right]^{\top}-\mathbf{q}}{\theta}} \\ &=\operatorname*{lim}_{\theta\to0}\frac{\left[s\left(\cos\frac{\theta}{2}-1\right)-\mathbf{v}^{T}\omega\sin\frac{\theta}{2},s\omega\sin\frac{\theta}{2}+\left(\cos\frac{\theta}{2}-1\right)\mathbf{v}+\mathbf{v}\times\boldsymbol{\omega}\sin\frac{\theta}{2}\right]^{\top}}{\theta} \\ &=\left[-\frac{1}{2}\mathbf{v}^{T}\boldsymbol{\omega},\frac{1}{2}s\boldsymbol{\omega}+\frac{1}{2}\mathbf{v}\times\boldsymbol{\omega}\right]^{\top} \\ &=\mathbf{q}\otimes\left[0,\frac{1}{2}\boldsymbol{\omega}\right]^{\top} \end{aligned}
θ→0limθq⊗Δq−q=θ→0limθ[scos2θ−vTωsin2θ,sωsin2θ+cos2θv+v×ωsin2θ]⊤−q=θ→0limθ[s(cos2θ−1)−vTωsin2θ,sωsin2θ+(cos2θ−1)v+v×ωsin2θ]⊤=[−21vTω,21sω+21v×ω]⊤=q⊗[0,21ω]⊤
*相似、仿射、射影变换
除了欧氏变换,3D空间还存在其他几种变换方式,只不过欧氏变换是最简单的。它们一部分和测量几何有关,因为在之后的讲解中可能会提到,所以先罗列出来。欧氏变换保持了向量的长度和夹角,相当于我们把一个刚体原封不动地进行了移动或旋转,不改变它自身的样子。其他几种变换则会改变它的外形。它们都拥有类似的矩阵表示。
(1)相似变换
相似变换比欧氏变换多了一个自由度,它允许物体进行均匀缩放,其矩阵表示为
T
S
=
[
s
R
t
0
T
1
]
T_S=\begin{bmatrix}sR&t\\ 0^T&1\end{bmatrix}
TS=[sR0Tt1]
注意,旋转部分多了一个缩放因子
s
s
s ,表示我们在对向量旋转之后,可以在
x
,
y
,
z
x,y,z
x,y,z 之三个坐标上进行均匀缩放。由于含有缩放,相似变换不再保持图形的面积不变。
你可以想象一个边长为1的立方体通过相似变换后,变成边长为10的样子(但仍然是立方体)。三维相似变换的集合也叫作相似变换群,记作 S i m ( 3 ) Sim(3) Sim(3)。
(2)仿射变换
仿射变换的矩阵形式如下:
T
A
=
[
A
t
0
T
1
]
T_A=\begin{bmatrix}A&t\\ 0^\mathsf{T}&1\end{bmatrix}
TA=[A0Tt1]
与欧氏变换不同的是,仿射变换只要求A是一个可逆矩阵,而不必是正交矩阵。仿射变换也叫正交投影。经过仿射变换之后,立方体就不再是方的了,但是各个面仍然是平行四边形。
(3)射影变换
射影变换是最一般的变换,它的矩阵形式为
T
P
=
[
A
t
a
T
v
]
T_P=\begin{bmatrix}A&t\\ a^T&v\end{bmatrix}
TP=[AaTtv]
它的左上角为可逆矩阵
A
A
A ,右上角为平移
t
t
t,左下角为缩放
a
T
a^T
aT。由于采用了齐次坐标,当
v
≠
0
v\not=0
v=0 时,我们可以对整个矩阵除以
v
v
v 得到一个右下角为1的矩阵;否则得到右下角为0的矩阵。因此,2D的射影变换一共有8个自由度,3D则共有15个自由度。
射影变换是现在讲过的变换中,形式最为一般的。从真实世界到相机照片的变换可以看成一个射影变换。读者可以想象一个原本方形的地板砖,在照片中是什么样子:首先,它不再是方形的。由于近大远小的关系,它甚至不是平行四边形,而是一个不规则的四边形。
下表总结了目前讲到的几种变换的性质。注意在“不变性质”中,从上到下是有包含关系的。例如,欧氏变换除了保体积,也具有保平行、相交等性质。
| 变换名称 | 矩阵形式 | 自由度 | 不变性质 |
|---|---|---|---|
| 欧式变换 | [ R t 0 T 1 ] \begin{bmatrix}R&t\\ \boldsymbol{0}^{\text{T}}&1\end{bmatrix} [R0Tt1] | 6 | 长度、夹角体积 |
| 相似变换 | [ s R t 0 T 1 ] \begin{bmatrix}sR&t\\ \boldsymbol{0}^{\mathsf{T}}&1\end{bmatrix} [sR0Tt1] | 7 | 体积比 |
| 仿射变换 | [ A t 0 T 1 ] \begin{bmatrix}A&t\\ 0^{\text{T}}&1\end{bmatrix} [A0Tt1] | 12 | 平行性、体积比 |
| 射影变换 | [ A t a T v ] \begin{bmatrix}A&t\\ a^{\mathsf T}&v\end{bmatrix} [AaTtv] | 15 | 接触平面的相交和相切 |
从真实世界到相机照片的变换是一个射影变换。
如果相机的焦距为无穷远,那么这个变换为仿射变换。不过,在详细讲述相机模型之前,我们只要对它们有个大致的印象即可。






















 755
755

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








