LR，SVM，决策树的对比

首先，LR、SVM、决策树都可以用来做分类的任务。为了做分类，我们试图寻找决策边界线或是一条曲线（不必是直线），在特征空间里区分两个类别。

一、LR，SVM，决策树直观区别

举个例子：
有一个样本，它包含三个变量：x1, x2和target。target有0和1两种值，取决于预测变量x1和x2的值。将数据绘制在坐标轴上。

这就是特征空间，观测值分布于其中。这里因为我们只有两个预测变量/特征，所有特征空间是二维的。你会发现两个类别的样本用不同颜色的点做了标记。我希望我们的算法能计算出一条直线/曲线来分离这个类别。

通过目测可知，理想的决策边界（分割曲线）是一个圆。实际决策边界形状的差异则是由于逻辑回归、决策树和支持向量机算法的差异引起的。

逻辑回归的决策边界总是一条直线（或者一个平面，在更高维度上是超平面）。我们样本数据用逻辑回归得到的结果将会是这样。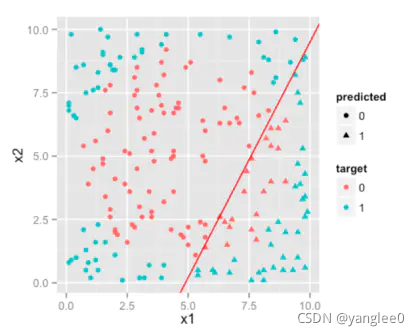
你会发现效果并不好。因为无论你怎么做，逻辑回归方法得到的决策边界总是线性的，并不能得到这里需要的环状边界。因此，逻辑回归适用于处理接近线性可分的分类问题。（虽然可以对变量做变换得到线性可分的结果，但我们在此不讨论这类情况。）

接着我们来看决策树如何处理这类问题。我们都知道决策树是按照层次结构的规则生成的。以我们的数据为例。

如果你仔细思考，这些决策规则x2 || const OR x1 || const 只是用平行于轴线的直线将特征空间切分，如下图所示。

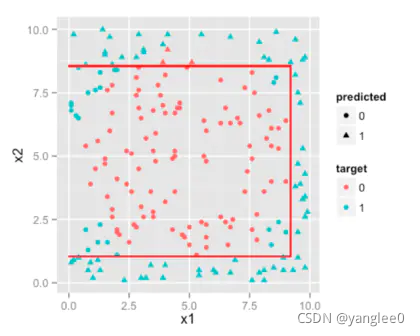
我们可以通过增加树的大小使它生长得更复杂，用越来越多的分区来模拟环状边界。

如果你继续增加树的尺寸，你会注意到决策边界会不断地用平行线围成一个环状区域。因此，如果边界是非线性的，并且能通过不断将特征空间切分为矩形来模拟，那么决策树是比逻辑回归更好的选择。

再来看看SVM的结果。SVM通过把你的特征空间映射到核空间，使得各个类别线性可分。这个过程更简单的解释就是SVM给特征空间又额外增加了一个维度，使得类别线性可分。这个决策边界映射回原特征空间后得到的是非线性决策边界。下图比我的解释更清楚。

你可以看到，一旦样本数据以某种方式增加了一个维度，我们就能用一个平面来分割数据（线性分类器），这个平面映射回原来的二维特征空间，就能得到一个环状的决策边界。

现在清楚各种区别了吧，但是还有一个问题。也就是说，在处理多维数据时，什么时候该选择何种算法？这个问题很重要，因为若是数据维度大于三，你就找不到简单的方法来可视化地呈现数据。往下看。

二、分析本身三者的优缺点

首先，我们来分析下逻辑回归（Logistic Regression）,它是解决工业规模问题最流行的算法，尽管与其他技术相比，其在效率和算法实现的易用性方面并不出众。

1、逻辑回归

逻辑回归非常便利并且很有用的一点在于，可以通过控制阈值来控制分类的结果。

逻辑回归的优点：

• 1、便利的观测样本概率分数；
  2、已有工具的高效实现；
  3、对逻辑回归而言，多重共线性并不是问题，它可以结合L2正则化来解决；
  4、逻辑回归广泛的应用于工业问题上（这一点很重要）。

逻辑回归的缺点：

• 1、当特征空间很大时，逻辑回归的性能不是很好；
  2、不能很好地处理大量多类特征或变量；
  3、对于非线性特征，需要进行转换；
  4、依赖于全部的数据（个人觉得这并不是一个很严重的缺点）。

2、决策树

决策树的优点：

• 1、直观的决策规则
  2、可以处理非线性特征
  3、考虑了变量之间的相互作用

决策树的缺点：

• 1、训练集上的效果高度优于测试集，即过拟合[随机森林克服了此缺点
  2、没有将排名分数作为直接结果

3、SVM

SVM的优点：

• 能够处理大型特征空间
  能够处理非线性特征之间的相互作用
  无需依赖整个数据

SVM的缺点：

• 当观测样本很多时，效率并不是很高
  有时候很难找到一个合适的核函数

三、如何选择这三种算法？

1、首当其冲应该选择的就是逻辑回归，如果它的效果不怎么样，那么可以将它的结果作为基准来参考；
2、然后试试决策树（随机森林）是否可以大幅度提升模型性能。即使你并没有把它当做最终模型，你也可以使用随机森林来移除噪声变量；
3、如果特征的数量和观测样本特别多，那么当资源和时间充足时，使用SVM不失为一种选择。