20实际80年代以来，由于微电子技术和各种电子器件的迅猛发展，使雷达的各分机及体系结构不断更新，雷达的数字化推进迅猛并将继续向雷达前端推进。
目前雷达可以明显改善严重杂波背景下检测小运动目标的性能。
相控雷达已经批量生产和广泛使用，具有多功能、多目标、搞数据率和高可靠性等优化。
4.1 概述
雷达接收机将天线接收到的微弱目标回波信号经过射频放大、混频、中频放大、检波及信号处理后，还要将回波中有关目标的信息与情报，经必要的加工在显示器上以只管的形式展示给操作人员，这一过程由 雷达终端 实现。
基本内容
-
目标数据的录取
-
数据处理
-
目标状态显示
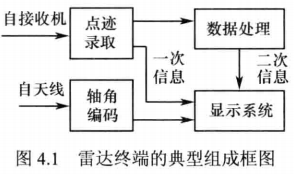
点迹录取用于实现来自接收机或信号处理机的雷达回波的确认，并提取其仰角、方位角、距离、速度等信息。
数据处理完成目标数据的关联、航迹处理、数据滤波等功能，实现对目标的连续跟踪。
轴角编码完成天线瞬时指向角的提取及其坐标系转换。
显示系统完成目标位置、运动状态、特征参数及空情态势等信息显示。 -
警戒雷达、引导雷达：
雷达终端的任务是发现目标、测定目标的位置坐标，根据回波的特点变化判断目标的性质掌握空情。 -
现代预警雷达、精密跟踪雷达：
采用数字式自动录取设备，在搜索状态发现和截获目标，在跟踪状态监视目标运动规律并监视雷达系统的工作状态。
雷达显示画面的坐标系通常分为极坐标和直角坐标两种方式。根据显示的坐标参数数量，可以分为一维显示和二维显示。
- 雷达终端显示器件：平板显示器件→液晶显示板LCD和等离子显示板PDP。
- 扫描方式：现代雷达显示器→随机扫描方式和光栅扫描方式。
雷达终端设备分为一次信息显示和二次信息显示：
- 一次：雷达目标回波的原始图像，模拟显示为主。
- 二次：经过加工处理的雷达回波数据信息，以及人工对雷达进行操作和控制的标志和数据等人机交互信息，数字显示为主。
4.2 传统雷达显示器的类型：
1、距离显示器
雷达距离显示器属于一维显示方式（距离维）其画面表现方式为：用屏幕上光电距参考点的水平偏移量表示目标的斜距，光电的垂直偏转幅度表示目标回波的强度。
类型：
（1）A型显示器：简称A显，采用直线扫描的方式。扫描线起点与发射脉冲同步，扫描线长度与雷达距离量程相对应，主波与回波之间的扫描线长度代表目标的斜距。
（2）A/R型显示器：为A型的改进形式，采用双踪直线扫描方式，上面一条扫描线和A型显示器相同，下面一条扫描线是上一条扫描线的局部扩展，用于提供目标回波更多的细节，提高人工距离录取精度。
（3）J型显示器：采用圆周扫描方式。与A型相似，所不同的是把扫描线由直线变为圆周。扫描圆周长对应雷达的距离量程，主波与回波沿顺时针方向的扫掠弧线长度对应目标的斜距。由于扫描圆周长一般大于屏幕直径，故其距离显示精度高于A型显示方式。
2、平面显示器
为二维显示方式（距离-方位维）。画面表现方式为：用屏幕上的光点的位置表示目标的平面位置坐标，光点的亮度表示目标回波的强度。平面显示器属于高度调制显示器。
平面显示器能够提供平面范围的目标分布情况，是使用最广泛的雷达显示器。人工录取目标坐标时，通常是在平面显示器上进行的。常用三种：
（1）PPI（Plan Position Indicator）或P型显示器：简称P显。采用径向扫描极坐标显示方式。以雷达站作为圆心（零距离），以正北方向作为方位角基准（零方位角）。径向扫描线方向为目标方位，沿顺时针方向度量。圆心作为距离基准，半径长度为距离量程，光点距圆心的距离为目标斜距，沿半径度量。光点大小对应目标尺寸，亮度对应目标强度。图中画面中心部分的大片光斑是近区的固定地物杂波回波所形成，较远的小亮弧则是运动目标，大的亮点是固定目标。
P显的画面分布情况与通用的平面地图是一致的，提供了360°范围内平面上的全部信息，所以P显也称为全景显示器或环形显示器。
（2）偏心PPI型显示器：简称偏心P显。移动原点偏离荧光屏的几何中心，以便在给定的方向上得到最大的扫描扩展，从而构成偏心P显。可以提高人工录取时的方位和距离测量精度。
（3）B型显示器：简称B显。平面显示器也可以用直角坐标方式来显示距离和方位，用横坐标表示方位，纵坐标表示距离，即B型显示器。通常横坐标不取全方位，而是雷达所监视的一个较小的方位范围。
3、高度显示器
二维显示方式（距离-仰角或距离-高度维）
在测高雷达和地形跟踪雷达中通称为E型显示器。其画面表现方式为：用平面上光点的横坐标表示距离，纵坐标表示目标仰角或高度。与B显配合，可实现目标的三维显示。
（1）E型显示器：用屏面上的光点的横坐标表示距离，纵坐标表示仰角。主要用于侧高雷达。
（2）RHI（Range-Height Indicator）型显示器：用屏面上光点的横坐标表示距离，纵坐标表示高度。用于精密跟踪雷达。
显示器类型的选择主要根据显示器的任务和显示的内容决定，例如，现实目标斜距采用A型、J型或A/R型；显示距离和方位采用P型，测高和地形跟踪采用E型等。
显示器 的对比度是指图像亮度和背景亮度的相对比值，定义为：
对
比
度
=
图
像
亮
度
−
背
景
亮
度
/
背
景
亮
度
×
100
对比度 = 图像亮度 - 背景亮度/背景亮度 × 100%
对比度=图像亮度−背景亮度/背景亮度×100
一般要求现在200%以上。
图像重显频率：为了使图像画面不出现闪烁，要求图像刷新的频率必须达到一定数值，一般要求大于每秒20-30次。
4.3 数字式雷达显示技术
传统雷达显示器由于扫描方式的特殊性，只能显示雷达回波的一次图像信息。
数字式雷达显示系统与通用的计算机信息显示系统相比，除了需要具备用于形成字符的字符产生器和用于生成线段的失量产生器以外，还需要一些专用的显示器件与技术。
数字式显示系统按其显示内容可分为：字符显示系统、图形图像显示系统及态势显示系统。
光栅扫描显示系统的显示器件采用光栅CRT、LCD或PDP等。扫描电路控制电子束以固定方式进行全屏逐点扫描，显示控制器控制特定点的会亮以实现信息显示。特点是具有高度的灵活性可编程性，信息显示容量大，是目前广泛采用的显示方式。
4.4 雷达图像展开
图像展开实际上就是图像放大，其目的就是为了观察图像的细节，提高显示分辨率，从而提高目标坐标录取精度。
LCD新型平板显示器件提交小、重量小、功耗小、无辐射，抗电磁干扰能力强等优点。
常用的LCD是有源矩阵型LCD，其像素的组成是按行、列的形式均匀排列的，其驱动是以行扫描信号和列寻址信号作用于被写入像素电极上的薄膜晶体管TFT有源电路，使之产生足够大的通断比，从而间接控制像素电极之间呈现TN型的液晶分子排列，达到显示的目的。显示器的控制电路采用大规模数字集成电路来实现，扫描方式多为矩阵选址方式。
4.5 雷达点迹录取
雷达系统对雷达信息处理过程主要有以下三个方面：
（1）从雷达接收机的输出中检测目标回波，判定目标存在。
（2）测量并录取目标的距离，角度，速度等信息。
（3）根据录取的目标信息，对目标进行编批，建立目标航迹，实现目标的稳定跟踪。
4.6 雷达数据处理
雷达数据处理的任务就是对雷达录取的目标点迹数据（也称目标的量测数据，包括目标的斜距、径向速度、方位角、俯仰角等）进行关联、滤波、预测等处理，形成目标运动轨迹（航迹），实现对目标的稳定跟踪。
由于测量设备存在噪声和干扰，雷达测得的目标量测数据总是含有随机误差，几遍清楚地直到目标的运动规律，也不能准确地求得目标当前坐标及下一时刻的预测坐标值，只能根据量测值对其进行统计意义上的估计。减少雷达测量过程中的随机误差，提高目标位置和运动参量的估计精度，更准确地预测目标下一时刻的状态。
数据处理可以看做是信号处理的延伸，信号处理是在较短的时间间隔内对同一目标的多个连续回波进行处理，提高回波的信噪比可以实现目标的有效检测，并给出目标位置和运动参数的估计（点迹数据）。
数据处理则是在相对较长的时间内对同一目标的多个点迹数据进行关联（多目标）、平滑滤波等处理，进一步提高了目标状态参量的估计精度。
在航迹被确认后，后续输入的点击将通过相关波门与各自的航迹建立关联。与某条航迹关联上的点迹将被认为属于该目标，根据对该目标所建立的状态方程，对该点迹数据进行相应的平滑滤波、预测外推处理，实现目标航迹的更新，同时调整下一个点迹可能出现的相关波门位置。实现目标的稳定连续跟踪，该稳定的目标航迹数据将通过显示设备呈现给雷达操纵人员。
相关波门是一个以目标预测位置为中心的区域，该区域决定了来自该目标的下一个点迹可能出现的位置范围。该区域的大小和形状一般根据目标的运动状态（速度、加速度、运动方向、扰动的大小）等因素来确定。
点击数据滤波是根据所假设的目标状态量测方程及目标运动状态方程来进行的。当状态量和量测量不在同一坐标系时还应当进行适当的坐标变换处理，称为点击数据预处理。根据目标运动状态的不同，采用不同的滤波跟踪算法。
- 在量测量与状态量呈线性关系情况下，采用线性滤波处理算法。典型的： α − β \alpha-\beta α−β滤波算法、 α − β − γ \alpha-\beta-\gamma α−β−γ滤波算法、卡尔曼滤波算法。当目标匀速运动时采用 α − β \alpha-\beta α−β算法；当目标做匀加速运动时，采用 α − β − γ \alpha-\beta-\gamma α−β−γ滤波算法。对于线性时变的非平稳运动过程，通常采用卡尔曼滤波算法。
- 在量测量与状态量成非线性关系（非线性量测方程）情况下，采用非线性滤波处理算法。常用的：扩展的卡尔曼滤波算法及粒子滤波算法。
目标运动与量测模型
目标运动模型是对目标运动规律在空间和时间上的数学描述。在目标跟踪中把目标看做是忽略其集合形状的点目标，并假设目标的状态及量测关系可以用数学方程描述。目标运动模型常以状态、时间的形式表示。
目标运动模型主要分为两大类：一类是非机动目标模型，主要有匀速CV模型和匀加速CA模型；另一类是机动目标模型，主要有Singer模型及均值自适应的“当前”统计模型等。
非机动目标模型
状态变量：目标位置、速度、加速度，随时间变化的随机过程。
状态方程：状态变量的变化规律，反映某时刻的状态变量与前一时刻状态变量的函数关系。
一般形式：
X
k
+
1
=
F
k
+
1
X
k
+
G
k
u
k
+
V
k
X_{k+1} = F_{k+1}X_k + G_ku_k+V_k
Xk+1=Fk+1Xk+Gkuk+Vk其中
X
k
∈
R
n
×
1
X_{k}\in R^{n×1}
Xk∈Rn×1为k时刻的状态，
F
k
+
1
,
k
∈
R
n
×
n
F_{k+1,k} \in R^{n×n}
Fk+1,k∈Rn×n是k时刻到k+1时刻的状态转移矩阵，
G
k
∈
R
n
×
p
G_k \in R^{n×p}
Gk∈Rn×p为输入控制项矩阵，
u
k
∈
R
p
×
1
u_k\in R^{p×1}
uk∈Rp×1为控制输入，
V
k
∈
R
n
×
1
V_k \in R^{n×1}
Vk∈Rn×1为状态噪声。
测量的不确定性导致目标量测值也是一个随着时间变化的随机过程。一般形式： Z k = H k X k + W k Z_k=H_kX_k+W_k Zk=HkXk+Wk式中， Z k ∈ R m × 1 Z_k\in R^{m×1} Zk∈Rm×1是k时刻的量测向量， H k ∈ R m × n H_k\in R^{m×n} Hk∈Rm×n为量侧矩阵， W K ∈ R m × 1 W_K\in R^{m×1} WK∈Rm×1为量测噪声。
状态噪声
V
k
V_k
Vk和量测噪声
W
k
W_k
Wk均假设为高斯白噪声向量序列且互不相关，其协方差矩阵分别记为
Q
k
Q_k
Qk和
R
k
R_k
Rk。
1、匀速（CV）运动模型
X
k
+
1
=
[
x
k
+
1
x
k
+
1
˙
]
=
[
1
T
0
1
]
[
x
k
x
k
˙
]
+
[
T
2
/
2
T
]
u
k
=
F
X
k
+
G
u
k
X_{k+1} = \begin{bmatrix} x_{k+1}\\ \dot{x_{k+1}} \end{bmatrix} = \begin{bmatrix}1 & T\\0 & 1\end{bmatrix}\begin{bmatrix}x_k\\\dot{x_k}\end{bmatrix} + \begin{bmatrix}T^2/2\\T\end{bmatrix}u_k = FX_k+Gu_k
Xk+1=[xk+1xk+1˙]=[10T1][xkxk˙]+[T2/2T]uk=FXk+Guk
T表示相邻两个时刻的间隔，
x
k
x_k
xk表示目标在k时刻所处的位置，
x
k
˙
\dot{x_k}
xk˙表示在k时刻的速度，X表示状态，F为状态转移矩阵，
u
k
u_k
uk为零均值的高斯白噪声随机序列，表示目标运动过程的加速度扰动。
k时刻对目标位置的测量值为
z
k
z_k
zk，则
z
k
=
x
k
+
w
k
=
[
1
0
]
[
x
k
x
k
˙
]
+
w
k
=
H
X
k
+
w
k
z_k = x_k + w_k = \begin{bmatrix}1&0\end{bmatrix}\begin{bmatrix}x_k\\\dot{x_k}\end{bmatrix} + w_k = HX_k+w_k
zk=xk+wk=[10][xkxk˙]+wk=HXk+wk
式中
w
k
w_k
wk为零均值方差为
σ
w
2
\sigma_w^2
σw2的高斯白噪声序列。
2、匀加速（CA）运动模型
设
x
k
，
x
k
˙
，
x
k
¨
x_k，\dot{x_k}，\ddot{x_k}
xk，xk˙，xk¨分别表示目标在k时刻所处的位置、速度及加速度，当目标以与加速运动时，其在k+1时刻的状态为：
x
k
+
1
=
x
k
+
x
k
˙
T
+
x
k
¨
T
2
/
2
+
u
k
T
2
/
2
x_{k+1} = x_k + \dot{x_k}T + \ddot{x_k}T^2/2+u_kT^2/2
xk+1=xk+xk˙T+xk¨T2/2+ukT2/2
x
k
+
1
˙
=
x
k
˙
+
x
k
¨
T
+
u
k
T
\dot{x_{k+1}} = \dot{x_k} + \ddot{x_k}T+u_kT
xk+1˙=xk˙+xk¨T+ukT
x
k
+
1
¨
=
x
k
¨
+
u
k
\ddot{x_{k+1}} = \ddot{x_k} +u_k
xk+1¨=xk¨+uk
转换为矩阵形式：
X
k
+
1
=
[
x
k
+
1
x
k
+
1
˙
x
k
+
1
¨
]
=
[
1
T
T
2
/
2
0
1
T
0
0
1
]
[
x
k
x
k
˙
x
k
¨
]
+
[
T
2
/
2
T
1
]
u
k
=
F
X
k
+
G
u
k
X_{k+1} = \begin{bmatrix}x_{k+1}\\\dot{x_{k+1}}\\\ddot{x_{k+1}}\end{bmatrix} = \begin{bmatrix}1&T&T^2/2\\0&1&T\\0&0 &1\end{bmatrix}\begin{bmatrix}x_k\\\dot{x_k}\\\ddot{x_k}\end{bmatrix} + \begin{bmatrix}T^2/2\\T\\1\end{bmatrix}u_k = FX_k + Gu_k
Xk+1=⎣⎡xk+1xk+1˙xk+1¨⎦⎤=⎣⎡100T10T2/2T1⎦⎤⎣⎡xkxk˙xk¨⎦⎤+⎣⎡T2/2T1⎦⎤uk=FXk+Guk
设k时刻对目标位置的测量值为
z
k
z_k
zk，则
z
k
=
x
k
+
w
k
=
[
1
0
0
]
[
x
k
x
k
˙
x
k
¨
]
+
w
k
=
H
W
k
+
w
k
z_k = x_k + w_k = \begin{bmatrix}1&0&0\end{bmatrix}\begin{bmatrix}x_k\\\dot{x_k}\\\ddot{x_k}\end{bmatrix}+w_k = HW_k+w_k
zk=xk+wk=[100]⎣⎡xkxk˙xk¨⎦⎤+wk=HWk+wk式中
w
k
w_k
wk仍为均值为0，方差为
σ
k
2
\sigma_k^2
σk2的高斯白噪声序列。
3、Singer模型
跟踪滤波算法
在上述状态方程和测量方程中，根据j时刻及以前的量测值对k时刻的状态 X k X_k Xk做出的某种估计记为 X k / j ^ \hat {X _ {k/j}} Xk/j^，则根据j的取值，估计问题可以分为以下几种情况：
- 当j=k时，为滤波问题。 X k / j ^ \hat {X _ {k/j}} Xk/j^为k时刻状态 X k X_k Xk的滤波值。
- 当j<k时，为预测问题。 X k / j ^ \hat {X _ {k/j}} Xk/j^为k时刻状态 X k X_k Xk的预测值。
- 当j>k时，为平滑问题。 X k / j ^ \hat {X _ {k/j}} Xk/j^为k时刻状态 X k X_k Xk的平滑值。
1、Kalman滤波
在所有的线性估计问题中，线性最小均方误差估计就是最优估计。根据最小均方误差准则，对于随即向量x机器观测z，当x、z为联合正态分布时，x的最小均方误差估计为其条件均值。
x
^
=
E
[
x
∣
z
]
=
E
(
x
)
+
P
x
z
P
z
z
−
1
[
z
−
E
(
z
)
]
\hat x = E[x|z] = E(x) + P_{xz}P_{zz}^{-1}[z-E(z)]
x^=E[x∣z]=E(x)+PxzPzz−1[z−E(z)]其估计误差协方差矩阵为
P
x
x
∣
z
=
E
[
(
x
−
x
^
)
(
x
−
x
^
)
T
∣
z
]
=
P
x
x
−
P
x
z
P
z
z
−
1
P
z
x
=
P
x
x
−
P
x
z
P
z
z
−
1
P
x
z
T
P_{xx|z} = E[(x-\hat x)(x-\hat x)^T |z]=P_{xx}-P_{xz}P_{zz}^{-1}P_{zx}=P_{xx}-P_{xz}P_{zz}^{-1}P_{xz}^T
Pxx∣z=E[(x−x^)(x−x^)T∣z]=Pxx−PxzPzz−1Pzx=Pxx−PxzPzz−1PxzT其中
P
x
z
，
P
z
z
、
P
x
x
P_{xz}，P_{zz}、P_{xx}
Pxz，Pzz、Pxx分别为x与z的互协方差矩阵及z、x的自协方差矩阵。
Kalman滤波的流程
假设系统模型是CV模型。由t1时刻的状态估计值
X
1
/
1
^
\hat{X_{1/1}}
X1/1^以匀速运动方式外推得到t2时刻状态的一步预测值
X
2
/
1
^
\hat{X_{2/1}}
X2/1^，利用t2时刻的观测值
Z
2
Z_2
Z2对一步预测值
X
2
/
1
^
\hat{X_{2/1}}
X2/1^进行修正，得到t2时刻状态估计值
X
2
/
2
^
\hat{X_{2/2}}
X2/2^，此过程一直重复进行。
航迹相关
航迹是对来自同一目标的点迹集合（量测集）经过滤波等处理后，由该目标在各个时刻的状态估计所形成的轨迹。
轨迹相关是将雷达接收到的点迹数据与已经建立的航迹进行配对关联，以确定点迹数据属于那一条航迹。因此，航迹相关主要应用于多目标跟踪中。当点迹与航迹关联后，目标的状态信息将通过前述的滤波算法得到更新。行及相关主要包含：设置相关波门的大小及形状；将雷达点迹与已建立的航迹进行一对一配对相关。
航迹相关的前提是已建立了相应目标的航迹起始状态，航迹起始是目标跟踪的第一步。
1、航迹起始
航迹自动起始的主要过程为，设计合适的航迹自动起始逻辑，通过门限判别是否建立暂时航迹，对已建立的暂时航迹进行确认。自动航迹起始一般采用滑窗法，当长度为n的时间窗内的1的个数达到或超过设定值，确认航迹开始，否则滑窗右移一次扫描，以上过程重复进行。
2、相关波门
相关波门是指以被跟踪目标的预测位置为中心，用来确定该目标的当前观测值可能出现的范围，该区域大小由正确接收回波的概率来确定。在确定波门大小和形状时要求真实的量测以较高的概率落入波门内，同时又要求无关的点迹尽量少地进入波门内。
二维坐标系下常见的相关波门形状：
直角坐标系下椭圆形波门，矩形波门，极坐标下扇形波门。三维坐标系下空间立体波门。
满足上式的
(
ρ
,
θ
)
(\rho,\theta)
(ρ,θ)落入波门内成为目标候选回波。式中
σ
ρ
2
和
σ
ρ
k
+
1
/
k
^
2
\sigma_\rho^2和\sigma_{\hat{\rho_{k+1/k}}}^2
σρ2和σρk+1/k^2分别表示距离方向测量误差的方差预测误差的方差，
σ
θ
2
和
σ
θ
k
+
1
/
k
^
2
\sigma_\theta^2和\sigma_{\hat{\theta{k+1/k}}}^2
σθ2和σθk+1/k^2分别表示方位向测量误差的方差及预测误差的方差。
点迹-航迹相关
主要算法有最近邻域关联滤波、概率数据关联滤波等。最近邻域关联滤波算法是一种利用先验统计知识进行点迹-航迹相关处理的算法。其工作原理是先设置相关波门，由相关波门初步删选接收到的回波作为候选波，以限制参与相关判别的回波数目。
最近邻域关联法计算简0单，适用于不太密集的多目标环境。但是在密集多目标环境中，容易垂涎错误关联导致误跟或丢失目标的现象，因为在这种情况下离目标预测位置最近的点迹往往不一定是目标的真是点迹，应将最近邻域关联滤波法与其他技术相结合或曹勇其他相关法实现点迹和航迹的可靠关联0。
航迹撤销
再对目标进行跟踪过程中，正在被跟踪的目标如果出了雷达监视区域后，对此目标跟踪将终结，对已建立的航迹予以撤销。相继数次没有新的目标点迹与之关联，此航迹予以撤销。
测量与跟踪坐标系
在现代雷达跟踪系统中，经常采用指教坐标系和雷达测量极坐标系这种混合坐标方式。优点是直角坐标系的参数变化率最小，且目标状态方程为线性方程。利用坐标变换，目标状态的预测和滤波可以在直角坐标系中方便地完成。
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
