1. 卷积
4 × 4 4×4 4×4 的输入矩阵 I I I 和 3 × 3 的卷积核 K K K：
- 在步长（stride）为 1 时，输出的大小为 ( 4 − 3 + 1 ) × ( 4 − 3 + 1 )
计算公式：
- 输入图片矩阵 I I I 大小： w × w w × w w×w
- 卷积核 K K K： k × k k × k k×k
- 步长 S S S： s s s
- 填充大小（padding）： p p p
o = ( w − k + 2 p ) s + 1 o = \frac{(w − k + 2p )}{s}+1 o=s(w−k+2p)+1
输出图片大小为： o × o o × o o×o
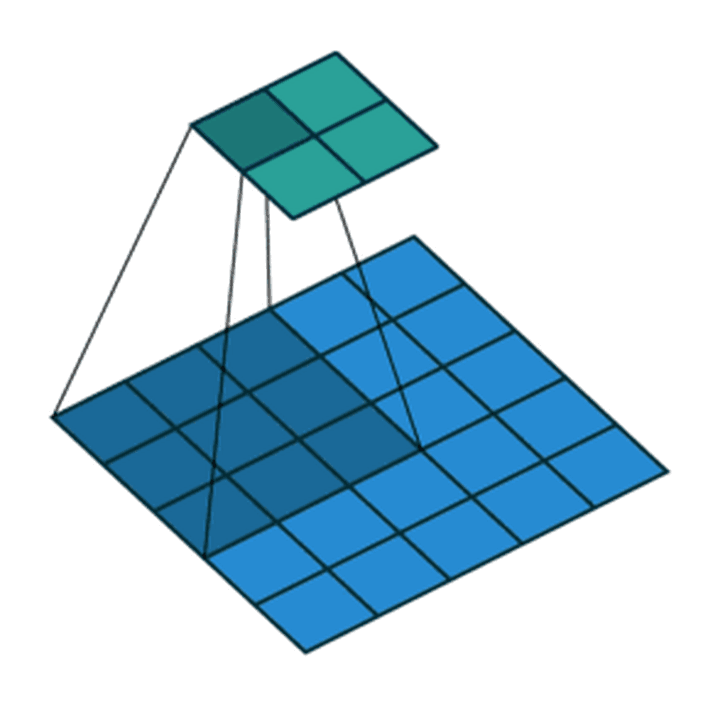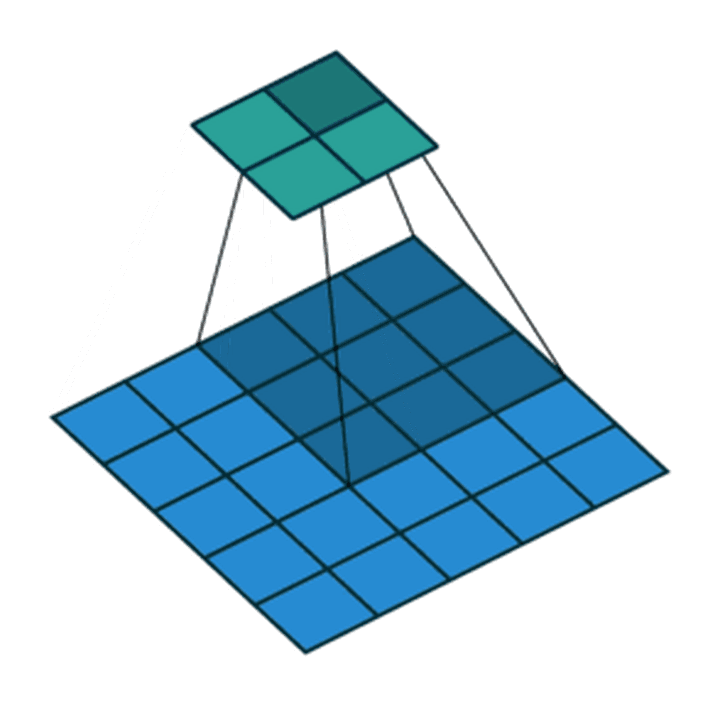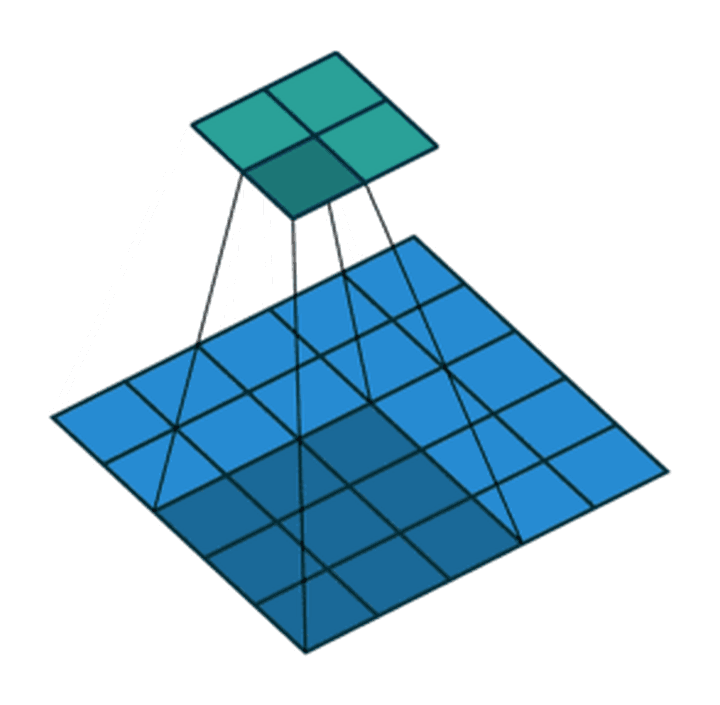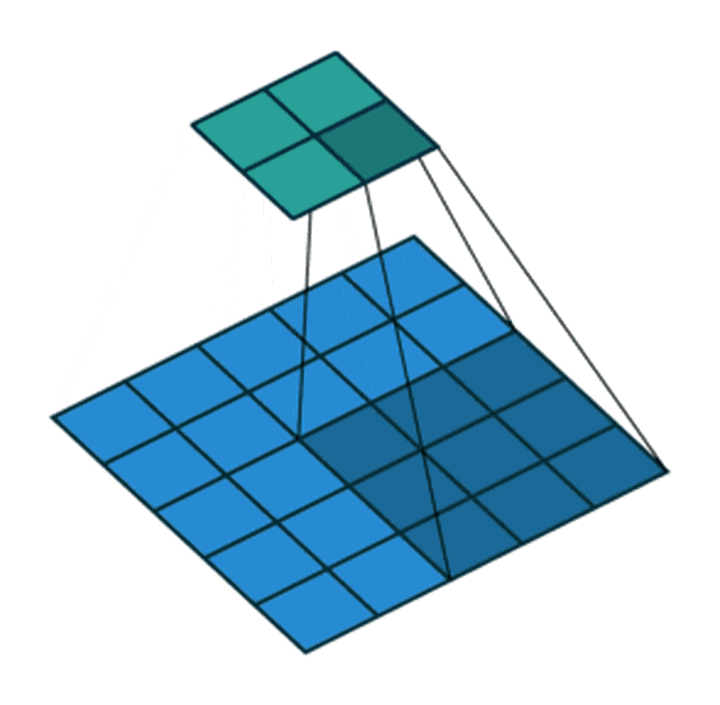
- 步长为2，卷积核为
3*3，p=0的卷积情况如下：
当卷积函数中padding='same'时，会动态调整
p
p
p 值，确保
o
=
w
o = w
o=w ，即保证输入与输出一致。例如：输入是 28*28*1 输出也为 28*28*1 。
- 步长为1，卷积核为
3*3，padding='same'的卷积情况如下：
实例：
7
∗
7
7*7
7∗7 的 input，
3
∗
3
3*3
3∗3 的 kernel，无填充，步长为1，则
o
=
(
7
−
3
)
1
+
1
o = \frac{(7 − 3 )}{1}+1
o=1(7−3)+1也即 output size 为
5
∗
5
5*5
5∗5
7
∗
7
7*7
7∗7 的 input，
3
∗
3
3*3
3∗3 的 kernel，无填充，步长为2，则
o
=
(
7
−
3
)
2
+
1
o = \frac{(7 − 3 )}{2}+1
o=2(7−3)+1也即 output size 为
3
∗
3
3*3
3∗3
扫一扫
919
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
