深度学习：深度复数网络(Deep Complex Networks)-从论文到pytorch实现

最新推荐文章于 2024-11-20 16:49:09 发布

Ten_yn

最新推荐文章于 2024-11-20 16:49:09 发布

阅读量2.4w

点赞数 51

分类专栏：从零单排-深度学习论文学习文章标签：深度复数网络深度学习论文复现 pytorch

本文链接：https://blog.csdn.net/qq_38290475/article/details/104630767

版权

从零单排-深度学习同时被 2 个专栏收录

12 篇文章

订阅专栏

论文学习

6 篇文章

订阅专栏

摘要：实数网络在图像领域取得极大成功，但在音频中，信号特征大多数是复数，如频谱等。简单分离实部虚部，或者考虑幅度和相位角都丢失了复数原本的关系。论文按照复数计算的定义，设计了深度复数网络，能对复数的输入数据进行卷积、激活、批规范化等操作。在音频信号的处理中，该网络应该有极大的优势。这里对论文提出的几种复数操作进行介绍，并给出简单的pytorch实现方法。

虽然叫深度复数网络，但里面的操作实际上还是在实数空间进行的。但通过实数的层实现类似于复数计算的操作。

主要参考文献

【1】“DEEP COMPLEX NETWORKS”

【2】论文作者给出的源码地址，使用Theano后端的Keras实现：“https://github.com/ChihebTrabelsi/deep_complex_networks”

【3】“https://github.com/wavefrontshaping/complexPyTorch” 给出了部分操作的Pytorch实现版本。

1. 关于复数卷积操作

复数卷积通过如下形式定义：
在这里插入图片描述
在具体实现中，可以使用下图所示的简单结构实现。
Alt

因此，利用pytorch的nn.Conv2D实现，严格遵守上面复数卷积的定义式：

class ComplexConv2d(Module):
    
    def __init__(self, input_channels, output_channels,
             kernel_sizes=3, stride=1, padding=0, dilation=0, groups=1, bias=True):
        super(ComplexConv2d, self).__init__()
        self.conv_real = Conv2d(input_channels, output_channels, kernel_size, stride, padding, dilation, groups, bias)
        self.conv_imag = Conv2d(input_channels, output_channels, kernel_size, stride, padding, dilation, groups, bias)
    
    def forward(self, input_real, input_imag):
        assert input_real.shape == input_imag.shape
        return self.conv_real(input_real) - self.conv_imag(input_imag), self.conv_imag(input_real) + self.conv_real(input_imag)

2. 关于复数激活函数

论文作者提出了一种复数激活函数——CReLU，同时又介绍了另外两种复数激活函数——modReLU和zReLU。
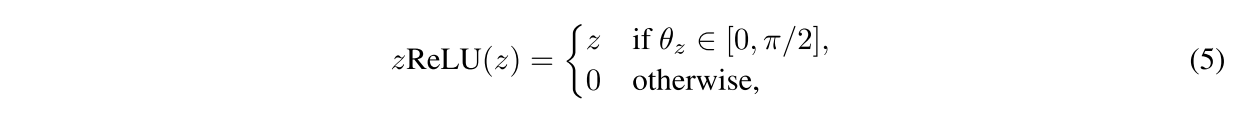
在这里插入图片描述

复数激活函数需要满足Cauchy-Riemann Equations才能进行复数微分操作，其中

modReLU不满足；
zReLU在实部为0，虚部大于0或者虚部为0，实部大于0的时候不满足，即在x和y的正半轴不满足；
CReLU只在实部虚部同时大于零或同时小于零的时候满足，即在第2、4象限不满足；

以作者提出的CReLU的实现为例：

from torch.nn.functional import relu

def complex_relu(input_real, input_imag):
    return relu(input_real), relu(input_imag)

3. 关于复数Dropout

复数Dropout个人感觉实部虚部需要同时置0，作者源码中没用到Dropout层。

所以【3】中的Dropout好像不太对。实现起来和普通的一样，共享两个Dropout层的参数即可。

4. 关于复数权重初始化

作者介绍了两种初始化方法的复数形式：Glorot、He初始化。

如原文介绍的，初始化时需要对幅度和相位分别初始化。

利用Pytorch实现，直接在源码上进行修改，_calculate_correct_fan()源码中有。

def complex_kaiming_normal_(tensor_real, tensor_imag, a=0, mode='fan_in'):

    fan = _calculate_correct_fan(tensor_real, mode)
    s = 1. / fan
    rng = RandomState()
    modulus = rng.rayleigh(scale=s, size=tensor.shape)
    phase = rng.uniform(low=-np.pi, high=np.pi, size=tensor.shape)
    weight_real = modulus * np.cos(phase)
    weight_imag = modulus * np.sin(phase)
    weight = np.concatenate([weight_real, weight_imag], axis=-1)

    with torch.no_grad():
        return torch.tensor(weight)

上述计算过程参考【1】和【2】，但这种两个张量的初始化不知道怎么直接使用init这样的形式，只能配合如下手动初始化方法食用。

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np

# 第一一个卷积层，我们可以看到它的权值是随机初始化的
w=torch.nn.Conv2d(2,2,3,padding=1)
print(w.weight)


# 第一种方法
print("1.使用另一个Conv层的权值")
q=torch.nn.Conv2d(2,2,3,padding=1) # 假设q代表一个训练好的卷积层
print(q.weight) # 可以看到q的权重和w是不同的
w.weight=q.weight # 把一个Conv层的权重赋值给另一个Conv层
print(w.weight)

# 第二种方法
print("2.使用来自Tensor的权值")
ones=torch.Tensor(np.ones([2,2,3,3])) # 先创建一个自定义权值的Tensor，这里为了方便将所有权值设为1
w.weight=torch.nn.Parameter(ones) # 把Tensor的值作为权值赋值给Conv层，这里需要先转为torch.nn.Parameter类型，否则将报错
print(w.weight)

5. 关于复数BatchNormalization

首先肯定不能用常规的BN方法，否则实部和虚部的分布就不能保证了。但正如常规BN方法，首先要对输入进行0均值1方差的操作，只是方法有所不同。

通过下面的操作，可以确保输出的均值为0，协方差为1，相关为0。
在这里插入图片描述

同时BN中还有 $\beta$ 和 $\gamma$ 两个参数。因此最终的BN结果如下。

核心的计算步骤及代码实现见下一节完整实现过程，参考【3】。

6. 完整模型搭建

使用复数卷积、BN、激活函数搭建一个简单的完整模型。

使用mnist数据集，用文中提到的方法生成虚部。

实际使用中音频、光学信号可以直接有复数谱作为输入。

import matplotlib.pyplot as plt
import numpy as np

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn import Module, Parameter, init
from torch.nn import Conv2d, Linear, BatchNorm2d
from torch.nn.functional import relu
from torchvision import datasets, transforms


def complex_relu(input_r, input_i):
    return relu(input_r), relu(input_i)

class ComplexConv2d(Module):

    def __init__(self,in_channels, out_channels, kernel_size=3, stride=1, padding = 0,
                 dilation=1, groups=1, bias=True):
        super(ComplexConv2d, self).__init__()
        self.conv_r = Conv2d(in_channels, out_channels, kernel_size, stride, padding, dilation, groups, bias)
        self.conv_i = Conv2d(in_channels, out_channels, kernel_size, stride, padding, dilation, groups, bias)

    def forward(self,input_r, input_i):
        assert(input_r.size() == input_i.size())
        return self.conv_r(input_r)-self.conv_i(input_i), self.conv_r(input_i)+self.conv_i(input_r)

class ComplexLinear(Module):

    def __init__(self, in_features, out_features):
        super(ComplexLinear, self).__init__()
        self.fc_r = Linear(in_features, out_features)
        self.fc_i = Linear(in_features, out_features)

    def forward(self,input_r, input_i):
        return self.fc_r(input_r)-self.fc_i(input_i), self.fc_r(input_i)+self.fc_i(input_r)

class _ComplexBatchNorm(Module):

    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True):
        super(_ComplexBatchNorm, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.affine = affine
        self.track_running_stats = track_running_stats
        if self.affine:
            self.weight = Parameter(torch.Tensor(num_features,3))
            self.bias = Parameter(torch.Tensor(num_features,2))
        else:
            self.register_parameter('weight', None)
            self.register_parameter('bias', None)
        if self.track_running_stats:
            self.register_buffer('running_mean', torch.zeros(num_features,2))
            self.register_buffer('running_covar', torch.zeros(num_features,3))
            self.running_covar[:,0] = 1.4142135623730951
            self.running_covar[:,1] = 1.4142135623730951
            self.register_buffer('num_batches_tracked', torch.tensor(0, dtype=torch.long))
        else:
            self.register_parameter('running_mean', None)
            self.register_parameter('running_covar', None)
            self.register_parameter('num_batches_tracked', None)
        self.reset_parameters()

    def reset_running_stats(self):
        if self.track_running_stats:
            self.running_mean.zero_()
            self.running_covar.zero_()
            self.running_covar[:,0] = 1.4142135623730951
            self.running_covar[:,1] = 1.4142135623730951
            self.num_batches_tracked.zero_()

    def reset_parameters(self):
        self.reset_running_stats()
        if self.affine:
            init.constant_(self.weight[:,:2],1.4142135623730951)
            init.zeros_(self.weight[:,2])
            init.zeros_(self.bias)

class ComplexBatchNorm2d(_ComplexBatchNorm):

    def forward(self, input_r, input_i):
        assert(input_r.size() == input_i.size())
        assert(len(input_r.shape) == 4)
        exponential_average_factor = 0.0


        if self.training and self.track_running_stats:
            if self.num_batches_tracked is not None:
                self.num_batches_tracked += 1
                if self.momentum is None:  # use cumulative moving average
                    exponential_average_factor = 1.0 / float(self.num_batches_tracked)
                else:  # use exponential moving average
                    exponential_average_factor = self.momentum


        if self.training:

            # calculate mean of real and imaginary part
            mean_r = input_r.mean([0, 2, 3])
            mean_i = input_i.mean([0, 2, 3])


            mean = torch.stack((mean_r,mean_i),dim=1)

            # update running mean
            with torch.no_grad():
                self.running_mean = exponential_average_factor * mean\
                    + (1 - exponential_average_factor) * self.running_mean

            input_r = input_r-mean_r[None, :, None, None]
            input_i = input_i-mean_i[None, :, None, None]

            # Elements of the covariance matrix (biased for train)
            n = input_r.numel() / input_r.size(1)
            Crr = 1./n*input_r.pow(2).sum(dim=[0,2,3])+self.eps
            Cii = 1./n*input_i.pow(2).sum(dim=[0,2,3])+self.eps
            Cri = (input_r.mul(input_i)).mean(dim=[0,2,3])

            with torch.no_grad():
                self.running_covar[:,0] = exponential_average_factor * Crr * n / (n - 1)\
                    + (1 - exponential_average_factor) * self.running_covar[:,0]

                self.running_covar[:,1] = exponential_average_factor * Cii * n / (n - 1)\
                    + (1 - exponential_average_factor) * self.running_covar[:,1]

                self.running_covar[:,2] = exponential_average_factor * Cri * n / (n - 1)\
                    + (1 - exponential_average_factor) * self.running_covar[:,2]

        else:
            mean = self.running_mean
            Crr = self.running_covar[:,0]+self.eps
            Cii = self.running_covar[:,1]+self.eps
            Cri = self.running_covar[:,2]#+self.eps

            input_r = input_r-mean[None,:,0,None,None]
            input_i = input_i-mean[None,:,1,None,None]

        # calculate the inverse square root the covariance matrix
        det = Crr*Cii-Cri.pow(2)
        s = torch.sqrt(det)
        t = torch.sqrt(Cii+Crr + 2 * s)
        inverse_st = 1.0 / (s * t)
        Rrr = (Cii + s) * inverse_st
        Rii = (Crr + s) * inverse_st
        Rri = -Cri * inverse_st

        input_r, input_i = Rrr[None,:,None,None]*input_r+Rri[None,:,None,None]*input_i, \
                           Rii[None,:,None,None]*input_i+Rri[None,:,None,None]*input_r

        if self.affine:
            input_r, input_i = self.weight[None,:,0,None,None]*input_r+self.weight[None,:,2,None,None]*input_i+\
                               self.bias[None,:,0,None,None], \
                               self.weight[None,:,2,None,None]*input_r+self.weight[None,:,1,None,None]*input_i+\
                               self.bias[None,:,1,None,None]

        return input_r, input_i

class ComplexNet(nn.Module):
    
    def __init__(self):
        super(ComplexNet, self).__init__()
        self.conv1 = ComplexConv2d(1, 20, 5, 2)
        self.bn  = ComplexBatchNorm2d(20)
        self.conv2 = ComplexConv2d(20, 50, 5, 2)
        self.fc1 = ComplexLinear(4*4*50, 500)
        self.fc2 = ComplexLinear(500, 10)
        
        self.bn4imag = BatchNorm2d(1)
        self.conv4imag = Conv2d(1, 1, 3, 1, padding=1)
             
    def forward(self,x):
        xr = x
        # imaginary part BN-ReLU-Conv-BN-ReLU-Conv as shown in paper
        xi = self.bn4imag(xr)
        xi = relu(xi)
        xi = self.conv4imag(xi)
        
        # flow into complex net
        xr,xi = self.conv1(xr,xi)
        xr,xi = complex_relu(xr,xi)
        
        xr,xi = self.bn(xr,xi)
        xr,xi = self.conv2(xr,xi)
        xr,xi = complex_relu(xr,xi)
#         print(xr.shape)
        xr = xr.reshape(-1, 4*4*50)
        xi = xi.reshape(-1, 4*4*50)
        xr,xi = self.fc1(xr,xi)
        xr,xi = complex_relu(xr,xi)
        xr,xi = self.fc2(xr,xi)
        # take the absolute value as output
        x = torch.sqrt(torch.pow(xr,2)+torch.pow(xi,2))
        return F.log_softmax(x, dim=1)
    
batch_size = 64
trans = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (1.0,))])
train_set = datasets.MNIST('../data', train=True, transform=trans, download=True)
test_set = datasets.MNIST('../data', train=False, transform=trans, download=True)
train_loader = torch.utils.data.DataLoader(train_set, batch_size= batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_set, batch_size= batch_size, shuffle=True)
    
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

model = ComplexNet().to(device)
print(model)

optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

# train steps
train_loss = []
for epoch in range(50):
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        train_loss.append(loss.item())
        if batch_idx % 100 == 0:
            print('Train Epoch: {:3} [{:6}/{:6} ({:3.0f}%)]\tLoss: {:.6f}'.format(
                epoch,
                batch_idx * len(data), 
                len(train_loader.dataset),
                100. * batch_idx / len(train_loader), 
                loss.item())
            )
            
plt.plot(train_loss)