本分类专栏博客系列是学习《深入浅出强化学习原理入门》的学习总结。
书籍链接:链接:https://pan.baidu.com/s/1p0qQ68pzTb7_GK4Brcm4sw 提取码:opjy
文章目录
基于策略梯度的强化学习方法
回顾一下,如图7.1所⽰为强化学习⽅法的分类⽰意图。

一、值函数与直接策略搜索
1.1 异同
- ⼴义值函数的⽅法包括策略评估和策略改善两个步骤。当值函数最优时,策略是最优的。此时的最优策略是贪婪策略。贪婪策略是指 arg max a Q θ ( s , a ) \mathop {\arg \max }\limits_a {Q_\theta }(s,a) aargmaxQθ(s,a),即在状态为 s s s 时,对应最⼤⾏为值函数的动作,它是⼀个状态空间向动作空间的映射, 该映射就是最优策略。利⽤这种⽅法得到的策略往往是状态空间向有限集动作空间的映射。
- 策略搜索是将策略参数化,即 π θ ( s ) {\pi _\theta }(s) πθ(s):利⽤参数化的线性函数或⾮线 性函数(如神经⽹络)表⽰策略,寻找最优的参数,使强化学习的⽬标 ——累积回报的期望 E [ ∑ t = 0 H R ( s t ) ∣ π θ ] E\left[ {\sum\nolimits_{t = 0}^H {R({s_t})|{\pi _\theta }} } \right] E[∑t=0HR(st)∣πθ] 最大。
在值函数的⽅法中,我们迭代计算的是值函数,再根据值函数改善策略;⽽在策略搜索⽅法中,我们直接对策略进⾏迭代计算,也就是迭代更新策略的参数值,直到累积回报的期望最⼤,此时的参数所对应的策略为最优策略。
1.2 优缺点
其实正是因为直接策略搜索⽅法⽐值函数⽅法拥有更多的优点,我们才有理由或动机去研究和学习并改进直接策略搜索 法。
- 直接策略搜索⽅法是对策略 π \pi π 进⾏参数化表⽰,与值函数⽅法中对值函数进⾏参数化表⽰相⽐,策略参数化更简单,有更好的收敛性。
- 利⽤值函数⽅法求解最优策略时,策略改善需要求解 arg max a Q θ ( s , a ) \mathop {\arg \max }\limits_a {Q_\theta }(s,a) aargmaxQθ(s,a) ,当要解决的问题动作空间很⼤或者动作为连续集时, 该式⽆法有效求解。
- 直接策略搜索⽅法经常采⽤随机策略,因为随机策略可以将探索直接集成到所学习的策略之中。
与值函数⽅法相⽐,策略搜索⽅法也普遍存在⼀些缺点,⽐如:
- 策略搜索的⽅法容易收敛到局部最⼩值;
- 评估单个策略时并不充分,⽅差较⼤。
最近⼗⼏年,学者们针对这些缺点正在探索各种改进⽅法。这些⽅法之间的关系可⽤图7.3表⽰:

由上图所示:
策略搜索⽅法按照是否利⽤模型可分为⽆模型的策略搜索⽅法和基于模型的策略搜索⽅法。
其中⽆模型的策略搜索⽅法根据策略是采⽤随机策略还是确定性策略可分为随机策略搜索⽅法和确定性策略搜索⽅法。
随机策略搜索⽅法最先发展起来的是策略梯度⽅法;但策略梯度⽅法存在学习速率难以确定的问题,为回避该问题,学者们⼜提出了基于统计学习的⽅法和基于路径积分的⽅法。但TRPO⽅法并没有回避该问题,⽽是找到了 替代损失函数——利⽤优化⽅法在每个局部点找到使损失函数单调⾮增的最优步⻓,我们在下⼀章再重点讲解。
下⾯我们分别从似然率的视⾓和重要性采样的视⾓推导策略梯度:
二、策略梯度的推导
2.1 从似然率的视⾓推导
用 τ \tau τ 表⽰⼀组状态-⾏为序列 s 0 , u 0 , . . . , s H , u H {s_0},{u_0},...,{s_H},{u_H} s0,u0,...,sH,uH。
符号 R ( τ ) = ∑ t = 0 H R ( s t , u t ) R(\tau ) = \sum\nolimits_{t = 0}^H {R({s_t},{u_t})} R(τ)=∑t=0HR(st,ut) 表⽰轨迹 τ \tau τ 的回报, P ( τ ; θ ) P(\tau ;\theta ) P(τ;θ) 表⽰轨迹 τ \tau τ 出现的概率;强化学习的⽬标函数可表⽰为
U ( θ ) = E ( ∑ t = 0 H R ( s t , u t ) ; π θ ) = ∑ τ P ( τ ; θ ) R ( τ ) U(\theta ) = E\left( {\sum\nolimits_{t = 0}^H {R({s_t},{u_t})} ;{\pi _\theta }} \right) = \sum\nolimits_\tau {P(\tau ;\theta )R(\tau )} U(θ)=E(∑t=0HR(st,ut);πθ)=∑τP(τ;θ)R(τ)
强化学习的⽬标是找到最优参数,使得:
max θ U ( θ ) = max θ ∑ τ P ( τ ; θ ) R ( τ ) \mathop {\max }\limits_\theta U(\theta ) = \mathop {\max }\limits_\theta \sum\nolimits_\tau {P(\tau ;\theta )R(\tau )} θmaxU(θ)=θmax∑τP(τ;θ)R(τ)
这时,策略搜索⽅法实际上变成了⼀个优化问题。解决优化问题有很多⽅法,⽐如最速下降法、⽜顿法、内点法等。
其中最简单、也最常⽤的是最速下降法,此处称为策略梯度的⽅法,即 θ n e w = θ o l d + α ∇ θ U ( θ ) {\theta _{new}} = {\theta _{old}} + \alpha {\nabla _\theta }U(\theta ) θnew=θold+α∇θU(θ),问题的关键是如何计算策略梯度 ∇ θ U ( θ ) {\nabla _\theta }U(\theta ) ∇θU(θ)。
我们对目标函数求导:
∇ θ U ( θ ) = ∇ θ ∑ τ P ( τ ; θ ) R ( τ ) = ∑ τ ∇ θ P ( τ ; θ ) R ( τ ) = ∑ τ P ( τ ; θ ) P ( τ ; θ ) ∇ θ P ( τ ; θ ) R ( τ ) = ∑ τ P ( τ ; θ ) ∇ θ P ( τ ; θ ) R ( τ ) P ( τ ; θ ) = ∑ τ P ( τ ; θ ) ∇ θ log P ( τ ; θ ) R ( τ ) \begin{array}{l} {\nabla _\theta }U(\theta ) = {\nabla _\theta }\sum\nolimits_\tau {P(\tau ;\theta )R(\tau )} \\\\ = \sum\nolimits_\tau {{\nabla _\theta }P(\tau ;\theta )R(\tau )} \\\\ = \sum\nolimits_\tau {\frac{{P(\tau ;\theta )}}{{P(\tau ;\theta )}}{\nabla _\theta }P(\tau ;\theta )R(\tau )} \\\\ = \sum\nolimits_\tau {P(\tau ;\theta )\frac{{{\nabla _\theta }P(\tau ;\theta )R(\tau )}}{{P(\tau ;\theta )}}} \\\\ = \sum\nolimits_\tau {P(\tau ;\theta ){\nabla _\theta }\log P(\tau ;\theta )R(\tau )} \end{array} ∇θU(θ)=∇θ∑τP(τ;θ)R(τ)=∑τ∇θP(τ;θ)R(τ)=∑τP(τ;θ)P(τ;θ)∇θP(τ;θ)R(τ)=∑τP(τ;θ)P(τ;θ)∇θP(τ;θ)R(τ)=∑τP(τ;θ)∇θlogP(τ;θ)R(τ)
最终策略梯度变成求 ∇ θ log P ( τ ; θ ) R ( τ ) {\nabla _\theta }\log P(\tau ;\theta )R(\tau ) ∇θlogP(τ;θ)R(τ)的期望,这可以利⽤经验平均估算。因此,当利⽤当前策略 π θ \pi_{\theta} πθ采样 m m m 条轨迹后,可以利⽤ m m m 条轨迹的经验平均逼近策略梯度:
∇ θ U ( θ ) ≈ g ^ = 1 m ∑ i = 1 m ∇ θ log P ( τ ; θ ) R ( τ ) {\nabla _\theta }U(\theta ) \approx \hat g = \frac{1}{m}\sum\limits_{i = 1}^m {{\nabla _\theta }\log P(\tau ;\theta )R(\tau )} ∇θU(θ)≈g^=m1i=1∑m∇θlogP(τ;θ)R(τ)
在计算策略梯度时,所用的数据都是在新的策略下采样得到的,这就要求每次梯度更新之后就要根据新的策略全部重新采样,并把之前的在旧策略下采样到的样本全都丢弃,这种做法对数据的利用率非常低,使得收敛的速度也极低。那么如何有效利用旧的样本呢?这就需要引入重要性采样 的概念。
2.2 从重要性采样的视⾓推导
⽬标函数为: U ( θ ) = E ( ∑ t = 0 H R ( s t , u t ) ; π θ ) = ∑ τ P ( τ ; θ ) R ( τ ) U(\theta ) = E\left( {\sum\nolimits_{t = 0}^H {R({s_t},{u_t})} ;{\pi _\theta }} \right) = \sum\nolimits_\tau {P(\tau ;\theta )R(\tau )} U(θ)=E(∑t=0HR(st,ut);πθ)=∑τP(τ;θ)R(τ)
利⽤参数 θ o l d \theta_{old} θold 产⽣的数据评估参数 θ \theta θ 的回报期望,由重要性采样得:
U ( θ ) = ∑ τ P ( τ ∣ θ o l d ) P ( τ ; θ ) P ( τ ∣ θ o l d ) R ( τ ) = E τ ∼ θ o l d [ P ( τ ∣ θ ) P ( τ ∣ θ o l d ) R ( τ ) ] \begin{array}{l} U(\theta ) = \sum\limits_\tau {P(\tau |{\theta _{old}})\frac{{P(\tau ;\theta )}}{{P(\tau |{\theta _{old}})}}R(\tau )} \\\\ = {E_{\tau \sim {\theta _{old}}}}\left[ {\frac{{P(\tau |\theta )}}{{P(\tau |{\theta _{old}})}}R(\tau )} \right] \end{array} U(θ)=τ∑P(τ∣θold)P(τ∣θold)P(τ;θ)R(τ)=Eτ∼θold[P(τ∣θold)P(τ∣θ)R(τ)]
导数为
∇ θ U ( θ ) = E τ ∼ θ o l d [ ∇ θ P ( τ ∣ θ ) P ( τ ∣ θ o l d ) R ( τ ) ] {\nabla _\theta }U(\theta ) = {E_{\tau \sim{\theta _{old}}}}\left[ {\frac{{{\nabla _\theta }P(\tau |\theta )}}{{P(\tau |{\theta _{old}})}}R(\tau )} \right] ∇θU(θ)=Eτ∼θold[P(τ∣θold)∇θP(τ∣θ)R(τ)]
令 θ = θ o l d \theta=\theta_{old} θ=θold,得到当前策略的导数:
∇ θ U ( θ ) ∣ θ = θ o l d = E τ ∼ θ o l d [ ∇ θ P ( τ ∣ θ ) ∣ θ o l d P ( τ ∣ θ o l d ) R ( τ ) ] = E τ ∼ θ o l d [ ∇ θ log P ( τ ∣ θ ) ∣ θ o l d R ( τ ) ] \begin{array}{l} {\nabla _\theta }U(\theta )|_{\theta = {\theta _{old}}}\\\\ = {E_{\tau \sim {\theta _{old}}}}\left[ {\frac{{{\nabla _\theta }P(\tau |\theta ){|_{{\theta _{old}}}}}}{{P(\tau |{\theta _{old}})}}R(\tau )} \right]\\\\ = {E_{\tau \sim {\theta _{old}}}}\left[ {{\nabla _\theta }\log P(\tau |\theta ){|_{{\theta _{old}}}}R(\tau )} \right] \end{array} ∇θU(θ)∣θ=θold=Eτ∼θold[P(τ∣θold)∇θP(τ∣θ)∣θoldR(τ)]=Eτ∼θold[∇θlogP(τ∣θ)∣θoldR(τ)]
从重要性采样的视⾓推导策略梯度,不仅得出与似然率的视⾓相同的 结果,更重要的是得到了原来⽬标函数新的损失函数: U ( θ ) = E τ ∼ θ o l d [ P ( τ ∣ θ ) P ( τ ∣ θ o l d ) R ( τ ) ] U(\theta ) = {E_{\tau \sim{\theta _{old}}}}\left[ {\frac{{P(\tau |\theta )}}{{P(\tau |{\theta _{old}})}}R(\tau )} \right] U(θ)=Eτ∼θold[P(τ∣θold)P(τ∣θ)R(τ)],下⾯我们重点从直观上理解⼀下似然率策略梯度。
2.3 直观理解似然率策略梯度
前⾯利⽤似然率⽅法推导得出策略梯度公式为 : ∇ θ U ( θ ) ≈ g ^ = 1 m ∑ i = 1 m ∇ θ log P ( τ ; θ ) R ( τ ) {\nabla _\theta }U(\theta ) \approx \hat g = \frac{1}{m}\sum\limits_{i = 1}^m {{\nabla _\theta }\log P(\tau ;\theta )R(\tau )} ∇θU(θ)≈g^=m1i=1∑m∇θlogP(τ;θ)R(τ)
下⾯分别阐述公式中的 ∇ θ log P ( τ ; θ ) 、 R ( τ ) {\nabla _\theta }\log P(\tau ;\theta )、R(\tau ) ∇θlogP(τ;θ)、R(τ)
- 第⼀项 ∇ θ log P ( τ ; θ ) {\nabla _\theta }\log P(\tau ;\theta ) ∇θlogP(τ;θ) 是轨迹 τ \tau τ 的概率随参数 θ \theta θ 变化最陡的⽅向。参数在该⽅向更新时,若沿着正⽅向,则该轨迹 τ \tau τ 的概率会变⼤;若沿着负⽅向更新,则该轨迹 τ \tau τ 的概率会变⼩。
- 第⼆项 R ( τ ) R(\tau ) R(τ) 控制了参数更新的⽅向和步⻓。 R ( τ ) R(\tau ) R(τ) 为正且越⼤则参数 更新后该轨迹的概率越⼤; R ( τ ) R(\tau ) R(τ) 为负,则降低该轨迹的概率,抑制该轨 迹的发⽣。
因此,从直观上理解策略梯度时,我们发现策略梯度会增加⾼回报路径的概率,减⼩低回报路径的概率。如图7.4所⽰,⾼回报区域的轨迹概率被增⼤,低回报区域的轨迹概率被减⼩。

2.4 策略梯度求解
前⾯推导出策略梯度的求解公式为:
∇ θ U ( θ ) ≈ g ^ = 1 m ∑ i = 1 m ∇ θ log P ( τ ; θ ) R ( τ ) {\nabla _\theta }U(\theta ) \approx \hat g = \frac{1}{m}\sum\limits_{i = 1}^m {{\nabla _\theta }\log P(\tau ;\theta )R(\tau )} ∇θU(θ)≈g^=m1i=1∑m∇θlogP(τ;θ)R(τ)
现在,我们解决似然率的梯度问题,即如何求 ∇ θ log P ( τ ; θ ) {\nabla _\theta }\log P(\tau ;\theta ) ∇θlogP(τ;θ)。
已知 τ = s 0 , u 0 , . . . , s H , u H \tau = {s_0},{u_0},...,{s_H},{u_H} τ=s0,u0,...,sH,uH,则轨迹的似然率可写成:
P ( τ ( i ) ; θ ) = ∏ t = 0 H P ( s t + 1 ( i ) ∣ s t ( i ) , u t ( i ) ) ⋅ π θ ( u t ( i ) ∣ s t ( i ) ) P({\tau ^{(i)}};\theta ) = \prod\limits_{t = 0}^H {P(s_{t + 1}^{(i)}|s_t^{(i)},u_t^{(i)}) \cdot {\pi _\theta }(u_t^{(i)}|s_t^{(i)})} P(τ(i);θ)=t=0∏HP(st+1(i)∣st(i),ut(i))⋅πθ(ut(i)∣st(i))
其中, P ( s t + 1 ( i ) ∣ s t ( i ) , u t ( i ) ) P(s_{t + 1}^{(i)}|s_t^{(i)},u_t^{(i)}) P(st+1(i)∣st(i),ut(i)) 表⽰动⼒学,⽆参数,因此可在求导过程中消掉。具体推导参⻅公式如下。
∇ θ log P ( τ ( i ) ; θ ) = ∇ θ log [ ∏ t = 0 H P ( s t + 1 ( i ) ∣ s t ( i ) , u t ( i ) ) ⋅ π θ ( u t ( i ) ∣ s t ( i ) ) ] = ∇ θ [ ∑ t = 0 H log P ( s t + 1 ( i ) ∣ s t ( i ) , u t ( i ) ) + ∑ t = 0 H log π θ ( u t ( i ) ∣ s t ( i ) ) ] = ∇ θ [ ∑ t = 0 H log π θ ( u t ( i ) ∣ s t ( i ) ) ] = ∑ t = 0 H ∇ θ log π θ ( u t ( i ) ∣ s t ( i ) ) \begin{array}{l} {\nabla _\theta }\log P({\tau ^{(i)}};\theta ) = {\nabla _\theta }\log \left[ {\prod\limits_{t = 0}^H {P(s_{t + 1}^{(i)}|s_t^{(i)},u_t^{(i)}) \cdot {\pi _\theta }(u_t^{(i)}|s_t^{(i)})} } \right]\\\\ = {\nabla _\theta }\left[ {\sum\limits_{t = 0}^H {\log } P(s_{t + 1}^{(i)}|s_t^{(i)},u_t^{(i)}) + \sum\limits_{t = 0}^H {\log {\pi _\theta }(u_t^{(i)}|s_t^{(i)})} } \right]\\\\ = {\nabla _\theta }\left[ {\sum\limits_{t = 0}^H {\log {\pi _\theta }(u_t^{(i)}|s_t^{(i)})} } \right]\\\\ = \sum\limits_{t = 0}^H {{\nabla _\theta }\log {\pi _\theta }(u_t^{(i)}|s_t^{(i)})} \end{array} ∇θlogP(τ(i);θ)=∇θlog[t=0∏HP(st+1(i)∣st(i),ut(i))⋅πθ(ut(i)∣st(i))]=∇θ[t=0∑HlogP(st+1(i)∣st(i),ut(i))+t=0∑Hlogπθ(ut(i)∣st(i))]=∇θ[t=0∑Hlogπθ(ut(i)∣st(i))]=t=0∑H∇θlogπθ(ut(i)∣st(i))
从上述公式的结果来看,似然率梯度转化为动作策略的梯度,与动⼒学⽆关,那么如何求解策略的梯度呢?
我们看⼀下常⻅的策略表⽰⽅法。
通常,随机策略可以写成确定性策略加随机部分,即 : π θ = μ θ + ε {\pi _\theta } = {\mu _\theta } + \varepsilon πθ=μθ+ε
⾼斯策略 ε ∼ N ( 0 , σ 2 ) \varepsilon \sim N(0,{\sigma ^2}) ε∼N(0,σ2),是均值为零,标准差为 σ \sigma σ 的⾼斯分布。
和值函数逼近⼀样,确定性部分通常表⽰成以下⽅式。
- 线性策略: μ ( s ) = ϕ ( s ) T θ \mu (s) = \phi {(s)^T}\theta μ(s)=ϕ(s)Tθ
- 径向基策略: π θ ( s ) = ω T ϕ ( s ) {\pi _\theta }(s) = {\omega ^T}\phi (s) πθ(s)=ωTϕ(s),其中, ϕ i ( s ) = exp ( − 1 2 ( s − μ i ) T D i ( s − μ i ) ) {\phi _i}(s) = \exp \left( { - \frac{1}{2}{{\left( {s - {\mu _i}} \right)}^T}{D_i}\left( {s - {\mu _i}} \right)} \right) ϕi(s)=exp(−21(s−μi)TDi(s−μi)),参数为: θ = { ω , μ i , d i } \theta = \{ \omega ,{\mu _i},{d_i}\} θ={ω,μi,di}
我们以确定性部分策略是线性策略为例说明 log π θ ( μ t ( i ) ∣ s t ( i ) ) \log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)}) logπθ(μt(i)∣st(i)) 是如何计算的。
首先, π ( μ ∣ s ) ∼ 1 2 π σ exp ( − ( μ − ϕ ( s ) T θ ) 2 2 σ 2 ) \pi (\mu |s) \sim \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left( { - \frac{{{{(\mu - \phi {{(s)}^T}\theta )}^2}}}{{2{\sigma ^2}}}} \right) π(μ∣s)∼2πσ1exp(−2σ2(μ−ϕ(s)Tθ)2) ,利⽤该分布采样,得到,然后将 ( s t ( i ) , μ t ( i ) ) (s_t^{(i)},\mu _t^{(i)}) (st(i),μt(i)) 代⼊,得:
∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) = ( μ t ( i ) − ϕ ( s t ( i ) ) T θ ) ϕ ( s t ( i ) ) σ 2 {\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)}) = \frac{{(\mu _t^{(i)} - \phi {{(s_t^{(i)})}^T}\theta )\phi (s_t^{(i)})}}{{{\sigma ^2}}} ∇θlogπθ(μt(i)∣st(i))=σ2(μt(i)−ϕ(st(i))Tθ)ϕ(st(i))
其中⽅差参数 σ 2 \sigma^2 σ2 ⽤来控制策略的探索性。
由此,推导出策略梯度的计算公式:
∇ θ U ( θ ) ≈ g ^ = 1 m ∑ i = 1 m ( ∑ t = 0 H ∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) R ( τ ( i ) ) ) {\nabla _\theta }U(\theta ) \approx \hat g = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\sum\limits_{t = 0}^H {{\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)})R({\tau ^{(i)}})} } \right)} ∇θU(θ)≈g^=m1i=1∑m(t=0∑H∇θlogπθ(μt(i)∣st(i))R(τ(i)))
上式的策略梯度是⽆偏的,但⽅差很⼤,我们在回报中引⼊常数基线b减⼩⽅差。
⾸先,证明当回报中引⼊常数b时,策略梯度不变,即:
∇ θ U ( θ ) ≈ g ^ = 1 m ∑ i = 1 m ∇ θ log P ( τ ( i ) ; θ ) R ( τ ( i ) ) = 1 m ∑ i = 1 m ∇ θ log P ( τ ( i ) ; θ ) ( R ( τ ( i ) ) − b ) \begin{array}{l} {\nabla _\theta }U(\theta ) \approx \hat g = \frac{1}{m}\sum\limits_{i = 1}^m {{\nabla _\theta }\log P({\tau ^{(i)}};\theta )R({\tau ^{(i)}})} \\\\ = \frac{1}{m}\sum\limits_{i = 1}^m {{\nabla _\theta }\log P({\tau ^{(i)}};\theta )(R({\tau ^{(i)}}) - b)} \end{array} ∇θU(θ)≈g^=m1i=1∑m∇θlogP(τ(i);θ)R(τ(i))=m1i=1∑m∇θlogP(τ(i);θ)(R(τ(i))−b)
证明:
E
[
∇
θ
log
P
(
τ
;
θ
)
b
]
=
∑
τ
P
(
τ
;
θ
)
∇
θ
log
P
(
τ
;
θ
)
b
=
∑
τ
P
(
τ
;
θ
)
∇
θ
P
(
τ
;
θ
)
b
P
(
τ
;
θ
)
=
∑
τ
∇
θ
P
(
τ
;
θ
)
b
=
∇
θ
(
∑
τ
P
(
τ
;
θ
)
b
)
=
∇
θ
b
=
0
\begin{array}{l} E[{\nabla _\theta }\log P(\tau ;\theta )b]\\\\ = \sum\limits_\tau {P(\tau ;\theta ){\nabla _\theta }\log P(\tau ;\theta )b} \\\\ = \sum\limits_\tau {P(\tau ;\theta )\frac{{{\nabla _\theta }P(\tau ;\theta )b}}{{P(\tau ;\theta )}}} \\\\ = \sum\limits_\tau {{\nabla _\theta }P(\tau ;\theta )b} \\\\ = {\nabla _\theta }\left( {\sum\limits_\tau {P(\tau ;\theta )b} } \right)\\\\ = {\nabla _\theta }b=0 \end{array}
E[∇θlogP(τ;θ)b]=τ∑P(τ;θ)∇θlogP(τ;θ)b=τ∑P(τ;θ)P(τ;θ)∇θP(τ;θ)b=τ∑∇θP(τ;θ)b=∇θ(τ∑P(τ;θ)b)=∇θb=0
然后,我们求使得策略梯度的⽅差最⼩时的基线b。
令: X = ∇ θ log P ( τ ( i ) ; θ ) ( R ( τ ( i ) ) − b ) X = {\nabla _\theta }\log P({\tau ^{(i)}};\theta )(R({\tau ^{(i)}}) - b) X=∇θlogP(τ(i);θ)(R(τ(i))−b),则方差为:
V a r ( X ) = E ( X − X ˉ ) 2 = E ( X 2 ) − [ E ( X ) ] 2 = E ( X 2 ) − X ˉ 2 Var(X) = E{(X - \bar X)^2} = E({X^2}) - {[E(X)]^2} = E({X^2}) - {{\bar X}^2} Var(X)=E(X−Xˉ)2=E(X2)−[E(X)]2=E(X2)−Xˉ2
⽅差最⼩处,⽅差对b的导数为零,即
∂ V a r ( X ) ∂ b = E ( X ∂ X ∂ b ) = 0 \frac{{\partial Var(X)}}{{\partial b}} = E\left( {X\frac{{\partial X}}{{\partial b}}} \right) = 0 ∂b∂Var(X)=E(X∂b∂X)=0
其中 X ˉ = E ( X ) \bar X = E(X) Xˉ=E(X) 与 b b b ⽆关。
将 X X X 代⼊ E ( X ∂ X ∂ b ) = 0 E\left( {X\frac{{\partial X}}{{\partial b}}} \right) = 0 E(X∂b∂X)=0,得:
b = ∑ i = 1 m [ ( ∑ t = 0 H ∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) ) 2 R ( τ ) ] ∑ i = 1 m [ ( ∑ t = 0 H ∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) ) 2 ] b = \frac{{\sum\limits_{i = 1}^m {\left[ {{{\left( {\sum\limits_{t = 0}^H {{\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)})} } \right)}^2}R(\tau )} \right]} }}{{\sum\limits_{i = 1}^m {\left[ {{{\left( {\sum\limits_{t = 0}^H {{\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)})} } \right)}^2}} \right]} }} b=i=1∑m[(t=0∑H∇θlogπθ(μt(i)∣st(i)))2]i=1∑m[(t=0∑H∇θlogπθ(μt(i)∣st(i)))2R(τ)]
除了上⾯介绍的增加基线的⽅法外,修改回报函数也可以进⼀步减⼩ ⽅差,此处不再介绍。
引⼊基线后,策略梯度公式变成:
∇ θ U ( θ ) ≈ 1 m ∑ i = 1 m ( ∑ t = 0 H ∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) ( R ( τ ( i ) ) − b ) ) {\nabla _\theta }U(\theta ) \approx \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\sum\limits_{t = 0}^H {{\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)})(R({\tau ^{(i)}}) - b)} } \right)} ∇θU(θ)≈m1i=1∑m(t=0∑H∇θlogπθ(μt(i)∣st(i))(R(τ(i))−b))
其中, b b b 取上式。
在这个公式中,每个动作 u t ( i ) u_t^{(i)} ut(i) 所对应的 ∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) {\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)}) ∇θlogπθ(μt(i)∣st(i)) 都乘以相同的该轨迹的总回报 R ( τ ( i ) ) − b R({\tau ^{(i)}}) - b R(τ(i))−b,如图:
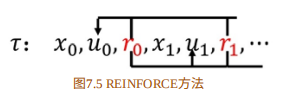
然⽽,当前的动作与过去的回报实际上是没有关系的,即:
E p [ ∂ θ log π θ ( u t ∣ x t , t ) r j ] = 0 , 对 于 j < t {E_p}[{\partial _\theta }\log {\pi _\theta }({u_t}|{x_t},t){r_j}] = 0,对于 j < t Ep[∂θlogπθ(ut∣xt,t)rj]=0,对于j<t
因此,我们可以修改引入基线后的策略梯度公式中的回报函数,有两种修改⽅法。
- G(PO)MDP
∇ θ U ( θ ) ≈ 1 m ∑ i = 1 m ∑ j = 0 H − 1 ( ∑ t = 0 j ∇ θ log π θ ( μ t ( i ) ∣ s t ( i ) ) ( r j − b j ) ) {\nabla _\theta }U(\theta ) \approx \frac{1}{m}\sum\limits_{i = 1}^m {\sum\limits_{j = 0}^{H - 1} {\left( {\sum\limits_{t = 0}^j {{\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)})({r_j} - {b_j})} } \right)} } ∇θU(θ)≈m1i=1∑mj=0∑H−1(t=0∑j∇θlogπθ(μt(i)∣st(i))(rj−bj))
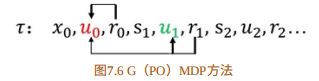
- 策略梯度理论
∇
θ
U
(
θ
)
≈
1
m
∑
i
=
1
m
∑
j
=
0
H
−
1
∇
θ
log
π
θ
(
μ
t
(
i
)
∣
s
t
(
i
)
)
(
∑
k
=
t
H
−
1
(
R
(
s
k
(
i
)
)
−
b
)
)
{\nabla _\theta }U(\theta ) \approx \frac{1}{m}\sum\limits_{i = 1}^m {\sum\limits_{j = 0}^{H - 1} {{\nabla _\theta }\log {\pi _\theta }(\mu _t^{(i)}|s_t^{(i)})\left( {\sum\limits_{k = t}^{H - 1} {(R(s_k^{(i)}) - b)} } \right)} }
∇θU(θ)≈m1i=1∑mj=0∑H−1∇θlogπθ(μt(i)∣st(i))(k=t∑H−1(R(sk(i))−b))
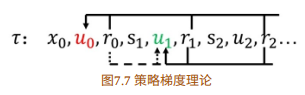
为了使⽅差最⼩,可以利⽤前⾯的⽅法求解相应的基线
b
b
b。
三、基于Tensorflow的策略梯度算法的实现
1. 策略神经⽹络的构建
构建⼀个神经⽹络,最简单的⽅法就是利⽤现有的深度学习软件,从 兼容性和通⽤性考虑,我们选择TensorFlow,待构建的策略⽹络结构如图 7.10所⽰。

该神经⽹络是最简单的前向神经⽹络,输⼊层为状态
s
s
s ,共
4
4
4 个神经 元,第⼀个隐藏层包括
10
10
10 个神经元,激活函数为ReLU;输出是动作的概率,动作有
2
2
2 个,因此第⼆层为
2
2
2 个神经元,没有激活函数;最后⼀层为 softmax 层。
将这话翻译成TensorFlow语⾔的表述如下。
def _build_net(self):
with tf.name_scope('input'):
# 创建占位符作为输入
self.tf_obs = tf.placeholder(tf.float32, [None,self.n_features], name="observations")
self.tf_acts = tf.placeholder(tf.int32, [None, ], name= "actions_num")
self.tf_vt = tf.placeholder(tf.float32, [None, ], name= "actions_value")
# 第一层
layer = tf.layers.dense(
inputs = self.tf_obs,
units = 10,
activation = tf.nn.tanh,
kernel_initializer = tf.random_normal_initializer(mean = 0, stddev = 0.3)
bias_initializer = tf.constant_initializer(0.1),
name = 'fc1',
)
#第二层
all_act = tf.layers.dense(
inputs = layer,
units = self.n_actions,
activation = None,
kernel_initializer = tf.random_normal_initializer(mean = 0, stddev = 0.3)
bias_initializer = tf.constant_initializer(0.1),
name = 'fc2',
)
#利用softmax函数得到每个动作的概率
self.all_act_prob = tf.nn.softmax(all_act, name='act_prob')
全部代码在 github (https://github.com/gxnk/reinforcement-learning-code)的policynet.py⽂件中。
2. 动作选择函数
动作选择函数是根据采样⽹络⽣成概率分布,利⽤该概率分布去采样 动作,具体代码如下。
#定义如何选择行为,即状态s时的行为采样,根据当前的额行为概率分布采样
def choose_action(self, observation):
prob_weight = self.sess.run(self.sll_act_prob,
feed_dict = {self.tf_obs:observation[np.newaxis,:]})
# 按照给定的概率采样
action = np.random.choice(range(prob_weight.shape[1]), p = prob_weight.ravel())
return action
其中函数 np.random.choice 是按照概率分布p=prob_weights.ravel() 采 样的函数。
3. 构建损失函数
理论部分我们已说明损失函数为
L = − E s ∼ ρ π , a ∼ π θ [ log π θ ( a ∣ s ) Q ω ( s , a ) ] = − ∫ p π θ o l d log q π θ Q ω ( s , a ) L = - {E_{s \sim {\rho ^\pi },a \sim {\pi _\theta }}}[\log {\pi _\theta }(a|s){Q^\omega }(s,a)] = - \int {{p_{{\pi _{{\theta _{old}}}}}}\log {q_{{\pi _\theta }}}{Q^\omega }(s,a)} L=−Es∼ρπ,a∼πθ[logπθ(a∣s)Qω(s,a)]=−∫pπθoldlogqπθQω(s,a)
即交叉熵乘以累积回报函数。以下是它的代码部分。
# 定义损失函数
with tf.name_scope('loss'):
neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(
logits = all_act, labels = self.tf_acts)
loss = tf.reduce_mean(neg_log_prob * self.tf_vt)
4. 累积回报函数 v v v 的处理
# 定义损失函数
with tf.name_scope('loss'):
neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits = all_act, labels = self.tf_acts)
loss = tf.reduce_mean(neg_log_prob * self.tf_vt)
def _discount_and_norm_rewards(self):
# 折扣回报和
discounted_ep_rs = np.zeros_like(self.ep_rs)
running_add = 0
for t in reversed(range(0, len(self.ep_rs))):
running_add = running_add * self.gamma + self.ep_rs[t]
discounted_ep_rs[t] = running_add
# 归一化
discounted_ep_rs -= np.mean(discounted_ep_rs)
discounted_ep_rs /= np.std(discounted_ep_rs)
return discounted_ep_rs
有了策略神经⽹络、动作选择函数、损失函数,累积回报函数,学习 的过程就简单了,只需要调⽤下⾯的语句即可。
# 定义训练,更新参数
with tf.name_scope('train'):
self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)
该训练过程为采⽤⾃适应动量的优化⽅法。学习优化的过程如下。
# 学习,以便更新策略网络参数,一个episode之后学一回
def learn(self):
# 计算一个 episode 的折扣回报
discounted_ep_rs_norm = self._discount_and_norm_rewards()
# 调用训练函数更新参数
self.sess.run(self.train_op, feed_dict={
self.tf_obs: np.vstack(self.ep_ops),
self.tf_acts: np.array(self.ep_as),
self.tf_vt: discounted_ep_rs_norm,
})
# 清空 episode 数据
self.ep_obs, self.ep_as, self.ep_rs = [], [], []
return discounted_ep_rs_norm
四、Tricks
3.1 策略梯度为什么取log?
在推倒策略梯度的时候用到 :一个函数求log,再求梯度 等于 这个函数先求梯度然后除以它本身。即: ∇ log f ( x ) = ∇ f ( x ) f ( x ) \nabla \log f(x) = \frac{{\nabla f(x)}}{{f(x)}} ∇logf(x)=f(x)∇f(x)
用 τ \tau τ 表⽰⼀组状态-⾏为序列 s 0 , u 0 , . . . , s H , u H {s_0},{u_0},...,{s_H},{u_H} s0,u0,...,sH,uH。
符号 R ( τ ) = ∑ t = 0 H R ( s t , u t ) R(\tau ) = \sum\nolimits_{t = 0}^H {R({s_t},{u_t})} R(τ)=∑t=0HR(st,ut) 表⽰轨迹 τ \tau τ 的回报, P ( τ ; θ ) P(\tau ;\theta ) P(τ;θ) 表⽰轨迹 τ \tau τ 出现的概率;强化学习的⽬标函数可表⽰为
U ( θ ) = E ( ∑ t = 0 H R ( s t , u t ) ; π θ ) = ∑ τ P ( τ ; θ ) R ( τ ) U(\theta ) = E\left( {\sum\nolimits_{t = 0}^H {R({s_t},{u_t})} ;{\pi _\theta }} \right) = \sum\nolimits_\tau {P(\tau ;\theta )R(\tau )} U(θ)=E(∑t=0HR(st,ut);πθ)=∑τP(τ;θ)R(τ)
若直接求梯度,则: ∇ U ( θ ) = ∑ τ R ( τ ) ∇ P ( τ ; θ ) \nabla U(\theta ) = \sum\nolimits_\tau {R(\tau )\nabla P(\tau ;\theta )} ∇U(θ)=∑τR(τ)∇P(τ;θ)
我们先看一下不转化为log的怎么求。从 τ 1 \tau^1 τ1 到 τ N \tau^N τN,每个轨迹求一个概率:
P ( τ n ; θ ) = p ( s 1 , u 1 , . . . , s n , u n ; θ ) = p ( s 1 , u 1 , s 2 ) p ( s 2 , u 2 , s 3 ) . . . p ( s n − 1 , u n − 1 , s n ) = p ( s 1 ) p ( u 1 ∣ s 1 ) p ( s 2 ∣ s 1 , u 1 ) . . . p ( s n − 1 ) p ( u n − 1 ∣ s n − 1 ) p ( s n ∣ s n − 1 , u n − 1 ) \begin{array}{l} P({\tau ^n};\theta ) = p({s_1},{u_1},...,{s_n},{u_n};\theta )\\\\ = p({s_1},{u_1},{s_2})p({s_2},{u_2},{s_3})...p({s_{n - 1}},{u_{n - 1}},{s_n})\\\\ = p({s_1})p({u_1}|{s_1})p({s_2}|{s_1},{u_1})...p({s_{n - 1}})p({u_{n - 1}}|{s_{n - 1}})p({s_n}|{s_{n - 1}},{u_{n - 1}}) \end{array} P(τn;θ)=p(s1,u1,...,sn,un;θ)=p(s1,u1,s2)p(s2,u2,s3)...p(sn−1,un−1,sn)=p(s1)p(u1∣s1)p(s2∣s1,u1)...p(sn−1)p(un−1∣sn−1)p(sn∣sn−1,un−1)
可以看出,如果要 n n n 从 1 1 1 到 N N N,我们要保存这些概率,先别说这些概率怎么计算出来,不断进行概率相乘,在策略最后的动作,无论多么出色, R R R 多大,这么多 0 ∼ 1 0\sim1 0∼1 的数乘起来,首先可能发生数据下溢,其次,出色的动作反而得不到概率上的提升,这是不对的。
那么加上 log ,就把数据相乘改为了相加,从策略的收敛速度上看,通过log运算,把原来 0 ∼ 1 0 \sim 1 0∼1 区间上的数映射到了 ( − ∞ , 0 ) (-\infty , 0) (−∞,0),并且没有改变数据的性质和相关关系;但是区间范围扩大了,一方面增大了梯度的大小,更新的更快了;另一方面,可以进一步拉大好的动作和差的动作之间的差距,使得策略尽可能朝着好的动作的方向去更新。






















 156
156











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








