常见的正则化方法和求解方法的研究。其中包括Lasso问题中绝对值x不可导的问题

欢迎大家来交流有什么问题可以在评论区发表，我看见了都会给与回复哦！

  正则化被用于控制模型的复杂度以防止过拟合。在训练机器学习模型时，过拟合是一个常见问题，指的是模型在训练数据上表现良好，但在未见过的测试数据上表现不佳的情况。正则化通过对模型的参数进行限制或惩罚，从而限制模型的复杂度，使其更加简单，从而有助于提高在未见过的数据上的泛化能力。

  常见的正则化技术包括 L1 正则化（Lasso 正则化）、L2 正则化（岭回归）和弹性网络。这些技术通过在模型的损失函数中引入额外的惩罚项来实现。具体而言，这里以损失函数残差的平方和举例：

L1 正则化（Lasso 正则化）：它通过在模型参数的绝对值之和上增加惩罚，即添加一个 L1 范数项。这通常导致一些模型参数变为零，从而实现特征选择的效果，使模型更加稀疏。

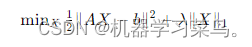
L2 正则化（岭回归）：它通过在模型参数的平方之和上增加惩罚，即添加一个 L2 范数项。这使得模型的参数趋向于较小的值，防止模型过于复杂，减少模型的方差，使模型更加平滑。

弹性网络：它结合了 L1 和 L2 正则化的效果，既可以获得稀疏性，又可以控制模型参数的大小。

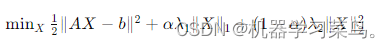
其中，∥AX−b∥²表示残差平方和，∥X∥ 1是 X 的 L1 范数，∥X∥ 2 是
X 的 L2 范数，λ 1 和 λ 2 是正则化参数，α 是混合参数，控制 L1 和 L2 正则化项的相对权重。

初次之外，还有一些惩罚项如下所示：

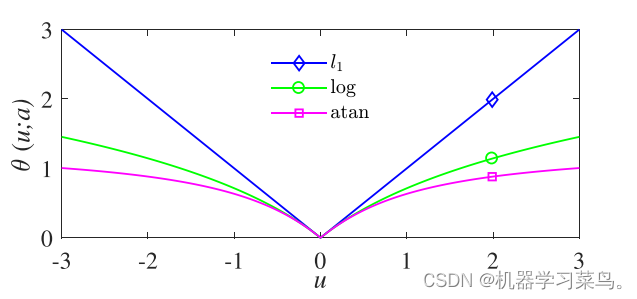
它们的图像如下：

在解决Lasso问题中 ∣x∣ 不可导问题时，有几种常见的方法：
  1.子梯度法（Subgradient Method）：子梯度法是一种广义的梯度下降方法，适用于非光滑凸优化问题。对于绝对值函数 ∣x∣，其子梯度可以在 x=0 处取任何值在区间 [−1,1] 内的点。因此，可以使用子梯度法来解决Lasso问题。
我们尝试使用python来实现它，我们定义一个L1惩罚项梯度的函数，用于返回|x|的导数。

import numpy as np

def l1_penalty_gradient(x):
    if x==0:
        return np.random.choice([-1, 1])
    else:
        return 1

def lasso_gradient_descent(A, b, lambd, learning_rate, max_iter, tol):
    m, n = A.shape
    x = np.zeros((n,1))  # 初始化参数向量为一维数组0
    for _ in range(max_iter):
        loss_gradient = A.T @ (A @ x - b)
        penalty_gradient=lambd * np.array([l1_penalty_gradient(xi) for xi in x]).reshape(-1,1)
        gradient=loss_gradient+penalty_gradient
        x -= learning_rate * gradient
        if np.linalg.norm(gradient) < tol:
            break
    return x
#
# # 示例数据
A = np.array([[1, 2], [3, 4], [5, 6]])
# print(A)
b = np.array([[3], [7], [11]])
# print(b)
lambd = 0.1
learning_rate = 0.01
max_iter = 1000
tol = 1e-6

# 调用梯度下降函数求解
result = lasso_gradient_descent(A, b, lambd, learning_rate, max_iter, tol)
print("参数向量 x：")
print(result)

  2.近似函数方法：如前面提到的，可以使用平滑的近似函数来代替绝对值函数，以便在非可导点处进行优化。这些近似函数通常是可微的，这样可以应用通常的梯度下降或其他优化算法进行求解。常见的近似函数包括Huber Loss函数和平方根惩罚函数。
  2.1.软阈值函数：：软阈值函数的出现是为了代替L1惩罚项，从而实现解的稀疏性性。
他的表达形式如下：

• 如果 x 的绝对值大于阈值 threshold，则将 x 的绝对值减去阈值，并保持 x 的符号不变。
• 如果 x 的绝对值小于等于阈值 threshold，则将 x 设为零。

这种操作使得软阈值函数在某些情况下可以将输入值“收缩”到零，从而实现信号的稀疏性或噪声的抑制。

1.如果使用使用软阈值函数求解Lasso问题的话，他就会变成经典的ISTA（迭代软阈值算法）算法。
软阈值算法的流程如下：

代码如下：

import numpy as np
#定义软阈值函数
def soft_thresholding(x, threshold):
    return np.sign(x) * np.maximum(np.abs(x) - threshold, 0)

def ista(A, b, lambda_, max_iter, alpha):
    n, _ = A.shape
    x = np.zeros((n, 1))  # 初始化参数向量
    for _ in range(max_iter):
        gradient = A.T @ (A @ x - b)  # 计算梯度
        x = soft_thresholding(x - alpha * gradient, lambda_ * alpha)  # 更新参数
    return x

# 示例数据
n = 10  # 特征维度
A = np.random.randn(n, n)  # 特征矩阵
true_theta = np.random.randn(n, 1)  # 真实参数
b = A @ true_theta + 0.1 * np.random.randn(n, 1)  # 观测结果（带噪声）
lambda_ = 0.1  # Lasso正则化参数
max_iter = 1000  # 最大迭代次数
alpha = 0.01  # 学习率

# 使用ISTA算法求解Lasso问题
estimated_theta = ista(A, b, lambda_, max_iter, alpha)
print("Estimated theta:")
print(estimated_theta)

2.后面有人嫌弃它的收敛速度不够快，提出了加速版本的ista算法，也就是FISTA算法，这个F在这里就是fast的意思，FISTA算法之所以快的原因是因为它引入了加速度项，通过引入了一个动量因子 α 来加速收敛，其中α(k)是前两个解β(k-1)、β(k-2)的特定线性组合。这个动量项可以使得迭代过程更加平滑，加速了算法的收敛。
α(k)的表达方式如下：

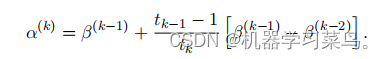
ISTA和FISTA的主要区别在于: ISTA是一种一阶方法，它仅使用直接前一个解的梯度。另一方面，FISTA是一种加速的一阶算法方法，它利用前两个解的梯度，以便更好的从历史中学习。
它的迭代过程如下所示：

可以看出每次计算梯度的时候使用的是加速度项α，而不是直接的β，而α是它前两个解的线性组合。
这里我们解释一下为什么引入了前两项的梯度信息就会变快的原因。
  具体来说，β(k−1)−β(k−2) 表示当前步骤与前一步的差值。如果当前步骤与前一步的梯度方向一致（即两者之差为正），那么动量项将增强当前步骤的更新方向，加速收敛；如果当前步骤与前一步的梯度方向相反（即两者之差为负），那么动量项将减弱当前步骤的更新方向，使得收敛更加平缓，避免了过度震荡。这种机制使得 FISTA 在迭代过程中可以更加灵活地适应目标函数的特性，从而更快地找到最优解。
接下来，我们给出fista算法的代码实现：

import numpy as np

def soft_thresholding(x, T):
    return np.maximum(np.abs(x) - T, 0) * np.sign(x)

def fista(y, X, L, lambda_, max_iterations):
    n, p = X.shape
    beta = np.zeros(p)
    alpha = np.copy(beta)
    t_prev = 1
    t = 1

    for k in range(1, max_iterations + 1):
        gradient = -X.T @ (y - X @ alpha) / n
        beta_new = soft_thresholding(alpha - (1 / L) * gradient, lambda_ / L)
        t_new = (1 + np.sqrt(1 + 4 * t ** 2)) / 2
        alpha = beta_new + (t_prev-1 / t_new) * (beta_new - beta)
        beta = np.copy(beta_new)
        t_prev = t
        t = t_new

    return beta

# 示例用法：
# 假设 y 和 X 是你的目标向量和特征矩阵
y = np.random.randn(100)
X = np.random.randn(100, 20)

# 设置超参数
L = np.max(X.T @ X) / len(y)
lambda_ = 0.1
max_iterations = 100

# 运行 FISTA 算法
result = fista(y, X, L, lambda_, max_iterations)

print(result)

3.为了摆脱|x|的不可微性，Schmidt等人（2007年）提出了其替代函数之一：

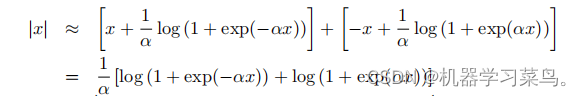
这个代替函数的图像如下所示:

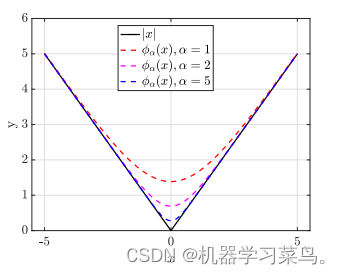
可以看出当α等于5时，他的图像很接近于|x|的图像。
而求解这个log近似函数，就变成了经典的SLA（平滑的1）算法:
他的迭代过程描述如下：

这里就是使用了log近似替代函数，也和fista一样，引入了Nesterov加速的思想，引入了前两阶的梯度信息，然后使用梯度下降算法进行迭代。
具体算法描述如下:

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def smooth_L1_gradient(x, alpha):
    return  (sigmoid(alpha * x) - sigmoid(-alpha * x))

def SLA(y, X, alpha, lambd, max_iterations=1000):
    n, p = X.shape
    mu = (np.max(np.sum(X**2, axis=0)) / np.sqrt(n) + lambd * alpha / 2) ** -1
    # Initialization
    beta = np.zeros(p)
    beta_prev=np.copy(beta)
    # Main optimization loop
    for k in range(1, max_iterations + 1):
        w = beta + (k - 2) / (k + 1) * (beta - beta_prev)
        grad_sq_loss = -X.T @ (y - X @beta) / n
        grad_smooth_L1 = lambd * smooth_L1_gradient(w, alpha_)
        grad = grad_sq_loss + grad_smooth_L1
        beta_prev = np.copy(beta)
        beta = w - mu * grad

    return beta

# Example usage:
# Assuming y and X are your target vector and feature matrix
y = np.random.randn(100)
X = np.random.randn(100, 20)

# Set hyperparameters
alpha = 0.01
lambd = 0.01
alpha_=5
# Run SLA algorithm
result = SLA(y, X, alpha, lambd)

print(result)

这里使用sigmoid函数来表达近似函数的导数。

3.次梯度法（Subgradient Method）： 次梯度法是子梯度法的一个特例，在处理非光滑凸优化问题时也是一种常见的方法。次梯度法是在每一步中从梯度的下界中选择一个子梯度，从而在优化过程中向着目标函数的最小值方向前进。
代码如下所示：

import numpy as np


def lasso_subgradient(X, y, lambda_, max_iter, tol):
    n, p = X.shape
    beta = np.zeros(p)
    step_size = 1 / (np.linalg.norm(X, ord=2) ** 2)

    for iter in range(max_iter):
        # 计算次梯度
        subgradient = np.dot(X.T, np.dot(X, beta) - y) + lambda_ * np.sign(beta)

        # 更新参数
        beta -= step_size * subgradient

        # 检查收敛条件
        if np.linalg.norm(subgradient, ord=np.inf) < tol:
            break

    return beta


# 示例数据
np.random.seed(0)
n = 100
p = 20
X = np.random.randn(n, p)
true_beta = np.random.randn(p)
y = np.dot(X, true_beta) + 0.1 * np.random.randn(n)
lambda_ = 0.1
max_iter = 1000
tol = 1e-5

# # 使用次梯度法求解Lasso问题
estimated_beta = lasso_subgradient(X, y, lambda_, max_iter, tol)
print("Estimated beta:", estimated_beta)

4.增广拉格朗日方法（Augmented Lagrangian Method）：增广拉格朗日方法是一种通过引入拉格朗日乘子来将带有不等式约束的优化问题转化为一个无约束问题的方法。这种方法也可以用于Lasso问题中的绝对值不可导情况，通过引入拉格朗日乘子，将原问题转化为一个等价的带有惩罚项的优化问题，然后使用迭代方法进行求解。

• 在ADMM中，将原始问题分解为若干个子问题，然后交替求解这些子问题直到收敛。
• ADMM在每一步迭代中，需要解决原始问题的两个子问题，一个是对原始变量的优化，另一个是对拉格朗日乘子的优化。
• ADMM的优点在于可以将大规模问题有效地分解成小规模子问题进行求解，每个子问题的求解相对简单，且可以并行化处理。
• 交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）
  代码如下：

import numpy as np


def soft_threshold(x, threshold):
    return np.sign(x) * np.maximum(np.abs(x) - threshold, 0)


def admm_lasso(A, b, rho, alpha, max_iter=100, tol=1e-4):
    n, d = A.shape
    x = np.zeros(d)
    z = np.zeros(d)
    u = np.zeros(d)

    Atb = np.dot(A.T, b)
    L = np.linalg.cholesky(np.dot(A.T, A) + rho * np.identity(d))#计算（ATA+p）

    for _ in range(max_iter):
        # Update x
        q = Atb + rho * (z - u)
        x = np.linalg.solve(L.T, np.linalg.solve(L, q))

        # Update z
        z_old = z.copy()
        z = soft_threshold(x + u, alpha / rho)

        # Update u
        u += x - z

        # Check convergence
        primal_residual = np.linalg.norm(x - z)
        dual_residual = np.linalg.norm(rho * (z - z_old))
        if primal_residual < tol and dual_residual < tol:
            break

    return x


# Example usage
np.random.seed(42)
n = 100
d = 50
A = np.random.randn(n, d)
true_coef = np.random.randn(d)
b = np.dot(A, true_coef) + 0.1 * np.random.randn(n)
alpha = 0.1
rho = 1.0

coef = admm_lasso(A, b, rho, alpha)
print("Estimated coefficients:", coef)