基2时间抽取FFT算法推导，及C语言实现

最新推荐文章于 2023-11-30 20:28:58 发布

90後_小熊大

最新推荐文章于 2023-11-30 20:28:58 发布

阅读量1.4w

点赞数 15

分类专栏：信号处理文章标签：信号处理

本文链接：https://blog.csdn.net/qq_38677310/article/details/99663883

版权

信号处理专栏收录该内容

2 篇文章 1 订阅

订阅专栏

1. 基2时间抽取FFT算法推导

设序列 $x[k]$ 的长度为 $N=2^{M}$ ， $M$ 为正整数,如果序列的长度不满足这个条件，可将序列 $x[k]$ 补0以满足该条件。对长度为N的序列 $x[k]$ 进行时间抽取，将其分解为两个长度为 $\frac{N}{2}$ 点的序列。两个长度 $\frac{N}{2}$ 点的序列分别为：

$x_{1}[k]=x[2k]$

$x_{2}[k]=x[2k+1],\, \, k=0,1,...,\frac{N}{2}$

其中 $x_{1}[k]$ 是序列 $x[k]$ 中的偶数点构成的序列， $x_{2}[k]$ 是序列 $x[k]$ 中的奇数点构成的序列。

对进行DFT得：

$\begin{align*} X[m] &= DFT(x[k]) = \sum_{k=0}^{N-1} x[k] W_{N}^{km}\\ &=\sum_{k=0}^{\frac{N}{2}-1} x[2k] W_{N}^{2km} + \sum_{k=0}^{\frac{N}{2}-1} x[2k+1] W_{N}^{(2k+1)m} \\ &=\sum_{k=0}^{\frac{N}{2}-1} x_{1}[k] W_{N}^{2km} + W_{N}^{m}\sum_{k=0}^{\frac{N}{2}-1} x_{2}[k] W_{N}^{2km} \end{align*}$

由于旋转因子 $W_{N}^{mk}$ 具有可约性，即 $W_{N}^{2mk}=e^{-j\frac{4\pi}{N}mk}=e^{-j\frac{2\pi}{N/2}mk}=W_{N/2}^{mk}$

故上述式子可表示为：

$X[m] = \sum_{k=0}^{\frac{N}{2}-1}x_{1}[k]W_{N/2}^{km} + W_{N}^{m}\sum_{k=0}^{\frac{N}{2}-1}x_{2}[k]W_{N/2}^{km} =X_{1}[m]+W_{N}^{m}X_{2}[m]$

由于 $X_{1}[m]$ 和 $X_{2}[m]$ 都具有周期性，周期为 $\frac{N}{2}$ ，即：

$X_{1}[m+\frac{N}{2}] = X_{1}[m]$

$X_{2}[m+\frac{N}{2}] = X_{2}[m]$

并且旋转因子存在对称性： $W_{N}^{m+N/2} = e^{-j\pi}W_{N}^{m} = -W_{N}^{m}$

因此：

$\begin{align*} X[m+\frac{N}{2}] &= X_{1}[m+\frac{N}{2}] + W_{N}^{m+N/2}X_{2}[m+\frac{N}{2}]\\ &=X_{1}[m] - W_{N}^{m}X_{2}[m] \end{align*}$

综上所述，最终可以表示为：

$X[m] = X_{1}[m] + W_{N}^{m}X_{2}[m]$

$X[m+\frac{N}{2}] = X_{1}[m] - W_{N}^{m}X_{2}[m] ,\, \, m=0,1,...,\frac{N}{2}\overset{{\color{Red} (1)}}{\leftarrow}$

由式子(1)可知，将 $x[k]$ 按奇偶分解得到两个子序列 $x_{1}[k]$ 和 $x_{2}[k]$ ，就可以由两个子序列 $x_{1}[k]$ 和 $x_{2}[k]$ 对应的DFT合成序列 $x[k]$ 的DFT。

蝶形计算结构：

基2时间抽取FFT运算流图（N=8）：

总结：

1、计算长度为N的有限长序列的频谱，得到长度为N的频谱。

若采用传统的DFT算法，则每一个频谱分量分量需要进行N次复数乘法、N-1次复数加法，计算所有的N个频谱分量一共需要进行 $N^{2}$ 次复数乘法、 $N(N-1)$ 次复数加法。

若采用基2时间抽取的FFT算法，计算分为 $\log _{2}^{N}$ 级，每一级含有 $\frac{N}{2}$ 个蝶形运算，每个蝶形运算包含1次复数乘法，2次复数加法（减法是特殊的加法），一共需要 $\frac{N}{2}\log _{2}^{N}$ 次复数乘法， $N\log _{2}^{N}$ 次复数加法。

两种算法比较，随着N的增大，FFT算法相较于DFT算法能够大幅减少计算量，降低计算复杂度，提高计算效率，优势明显。

2、利用FFT进行运算时，对于输入的原始序列需要对其进行逆排序，再将排序后的序列作为计算输入。这是由于FFT再进行偶奇分解得到短序列的过程中，改变了原始序列的循序。

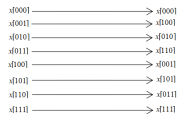
举个例子，假设N=8，用3位二进制表示序列的排序， $x[k_{2}k_{1}k_{0}]$ 经过逆排序后得到 $x[k_{0}k_{1}k_{2}]$ 其实也很好理解，每一次分解都进行偶奇判断，分解成偶数序列、奇数序列。

2. FFT算法——C语言实现

/*
 *    C语言实现 N=1024 FFT算法   
 *    验证序列：x[k]=sin(2*PI/N*k)
 *    
 *    Author: 90後_小熊大
 *    说明：代码经过实际验证，可以正常运行。
 *         代码仅供参考，欢迎学习交流！
 */

# include <stdio.h>
# include <math.h>

//定义PI
#define   PI   acos(-1.0)

//复数，结构体
typedef struct{
    float re;
    float im;
}Complex;

Complex x[1024];
Complex y[1024];


//-------------------------复数运算相关-----------------------------

Complex creatComplex(float re, float im){  //生成复数
    Complex z;
    z.re = re;
    z.im = im;
    return z;
}

Complex add(Complex z1, Complex z2){  //复数加法
    Complex z;
    z.re = z1.re + z2.re;
    z.im = z1.im + z2.im;
    return z;
}

Complex sub(Complex z1, Complex z2){  //复数减法
    Complex z;
    z.re = z1.re - z2.re;
    z.im = z1.im - z2.im;
    return z;
}

Complex mul(Complex z1, Complex z2){  //复数乘法
    Complex z;
    z.re = (z1.re * z2.re) - (z1.im * z2.im);
    z.im = (z1.re * z2.im) + (z1.im * z2.re);
    return z;
}

void printComplex_0(Complex z){       //打印函数
    if(z.re==0 && z.im==0)
        printf(" 0   ");
    else if(z.re!=0 && z.im==0)
    {
        if(z.re>0)
            printf(" %2.2f", z.re);
        else
            printf("%2.2f", z.re);
    }

    else if(z.re==0 && z.im!=0)
    {
        if(z.im>0)
            printf("       j%.2f", z.im);
        else if(z.im<0)
            printf("      -j%.2f", fabs(z.im));
    }
    else
    {
        if(z.im>0)
            printf("%2.2f + j%2.2f", z.re, z.im);
        else
            printf("%2.2f - j%2.2f", z.re, fabs(z.im));
    }
}

void printComplex_1(Complex z){       //打印函数
    int re, im;
    re = z.re;
    im = z.im;

    if(re==0 && im==0)
        printf("0\n");
    else if(re!=0 && im==0)
        printf("%.2f\n", re);
    else if(re==0 && im!=0)
    {
        if(im>0)
            printf("j%.2f\n",  fabs(im));
        else if(im<0)
            printf("-j%.2f\n", fabs(im));
    }
    else
    {
        if(im>0)
            printf("%.2f + j%.2f\n", re, im);
        else
            printf("%.2f - j%.2f\n", re, fabs(im));
    }
}

Complex creat_W(int N, int mk){       //生成旋转因子
    Complex W;
    W.re = cos(-(2 * PI/N * mk));
    W.im = sin(-(2 * PI/N * mk));
    return W;
}

//--------------------------------------------------------------------------


void Reverse_Order(unsigned int Input_Data){  //序列倒序运算
    unsigned int One_Binary_Data[10];
    unsigned int i;
    unsigned int Reverse_Order_Data;
    unsigned int label;

    label = Input_Data;

    for(i=0; i<10; i++){
        One_Binary_Data[i] = Input_Data % 2;
        Input_Data = Input_Data / 2;
    }

    Reverse_Order_Data = One_Binary_Data[0]*pow(2, 9) + One_Binary_Data[1]*pow(2, 8) + One_Binary_Data[2]*pow(2, 7) +\
                         One_Binary_Data[3]*pow(2, 6) + One_Binary_Data[4]*pow(2, 5) + One_Binary_Data[5]*pow(2, 4) +\
                         One_Binary_Data[6]*pow(2, 3) + One_Binary_Data[7]*pow(2, 2) + One_Binary_Data[8]*pow(2, 1) +\
                         One_Binary_Data[9]*pow(2, 0);

    y[label] = x[Reverse_Order_Data];
}


void FFT()   //Fast Fourier Transfortation
{
    int i, j;
    int M;
    int N, mk;                 //旋转矩阵参数
    Complex temp1, temp2;      //临时存放
    Complex W;                 //旋转矩阵
    for(i=0; i<10; i++)        //十层循环
    {
        for(j=0; j<512; j++)   //每层512个蝶形运算
        {
            M  = j / (int)pow(2, i);
            mk = j % (int)pow(2, i);
            N = pow(2, i+1);

            W = creat_W(N, mk);
            temp1 = y[(int)(j + M*pow(2, i))];
            temp2 = y[(int)(j + M*pow(2, i) + pow(2, i))];
            temp2 = mul(W, temp2);

            y[(int)(j + M*pow(2, i))] = add(temp1, temp2);
            y[(int)(j + M*pow(2, i) + pow(2, i))] = sub(temp1, temp2);
        }
    }
}


int main(){
    int Input_Label;
    int i;
    float temp;

    for(i=0; i<1024; i++){
        temp = sin(2*PI/1024*i);
        x[i] = creatComplex(temp, 0);
    }

    printf("++++++++++++++++++++++++++++++++++++++++++++++++\n");
    printf("+                                              +\n");
    printf("+     N=1024 FFT算法   Author: 90後_小熊大       +\n");
    printf("+                                              +\n");
    printf("+     验证序列：x[k]=sin(2*PI/N*k)             +\n");
    printf("+                                              +\n");
    printf("++++++++++++++++++++++++++++++++++++++++++++++++\n\n\n");
    printf("     原始序列:  --------- FFT ---------> 输出序列：\n\n");
    for(Input_Label=0; Input_Label<1024; Input_Label++){
        Reverse_Order(Input_Label);
    }

    FFT();

    for(i=0; i<1024; i++)
    {
        printf("x[%4d] = ", i);
        printComplex_0(x[i]);
        printf(" --------- FFT ---------> ");
        printf("X[%4d] = ", i);
        printComplex_1(y[i]);
    }
    return 0;
}

90後_小熊大

关注

15
点赞
踩
67

收藏

觉得还不错? 一键收藏
2
评论
基2时间抽取FFT算法推导，及C语言实现

1. 基2时间抽取FFT算法推导设序列的长度为，为正整数,如果序列的长度不满足这个条件，可将序列补0以满足该条件。对长度为N的序列进行时间抽取，将其分解为两个长度为点的序列。两个长度点的序列分别为：其中是序列中的偶数点构成的序列，是序列中的奇数点构成的序列。对进行DFT得： ...
复制链接

扫一扫