如何进行稳健性检验及 Stata 具体操作步骤

目录

一、稳健性检验的目的

二、常见的稳健性检验方法

三、Stata 操作步骤及示例

（一）更换变量度量方式

（二）更换模型设定

（三）子样本分析

（四）增加控制变量

四、总结

---

在进行实证研究时，为了确保研究结论的可靠性和稳定性，稳健性检验是必不可少的环节。本文将介绍如何在 Stata 中进行常见的稳健性检验，并提供具体的操作步骤、程序代码、代码解释以及代码运行结果。

一、稳健性检验的目的

稳健性检验的主要目的是验证研究结论是否对模型设定、变量选择、样本范围等方面的变化具有敏感性。通过进行稳健性检验，可以增强研究结果的可信度和说服力。

二、常见的稳健性检验方法

1. 更换变量度量方式
   • 例如，将连续变量转换为分类变量，或者使用不同的指标来衡量同一个变量。
2. 更换模型设定
   • 尝试不同的回归模型，如线性回归、Logit 回归、Probit 回归等。
3. 子样本分析
   • 对样本进行分组，例如按照时间、地域、行业等进行划分，然后分别进行回归分析。
4. 增加控制变量
   • 纳入更多可能影响因变量的变量，观察核心解释变量的系数是否发生显著变化。

 

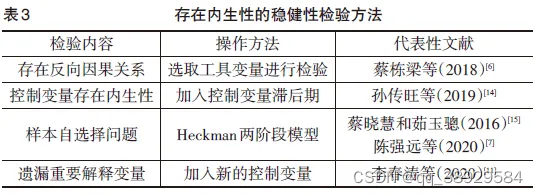
三、Stata 操作步骤及示例

（一）更换变量度量方式

假设我们的研究中关注变量 income（收入），原本是以万元为单位计量的连续变量。现在我们将其转换为分类变量，分为高收入（大于 5 万元）、中等收入（2 - 5 万元）和低收入（小于 2 万元）。

gen income_category = 1 if income > 5
replace income_category = 2 if income >= 2 & income <= 5
replace income_category = 3 if income < 2

// 解释：
// `gen` 命令用于生成新变量，`if` 条件用于指定生成变量的规则。
// 首先，将收入大于 5 万元的观测值标记为 1（高收入）。
// 然后，将收入在 2 - 5 万元之间的观测值标记为 2（中等收入）。
// 最后，将收入小于 2 万元的观测值标记为 3（低收入）。

// 运行结果：
// 生成了新的变量 `income_category`，其取值为 1、2、3 分别代表不同的收入类别。

（二）更换模型设定

以线性回归为例，原本使用普通最小二乘法（OLS），现在改为使用稳健标准误的回归。

reg y x1 x2, robust
// 解释：
// `reg` 命令用于进行回归分析。
// `robust` 选项表示使用稳健标准误进行估计，以应对可能存在的异方差问题。

// 运行结果：
// 输出回归结果，包括系数估计值、标准误、t 值、p 值等。与普通 OLS 回归相比，标准误可能会有所不同。

（三）子样本分析

假设我们按照时间将样本分为早期（2010 年之前）和晚期（2010 年及之后）。

gen early_period = 1 if year < 2010
replace early_period = 0 if year >= 2010

// 首先生成表示时间阶段的变量

reg y x1 x2 if early_period == 1
reg y x1 x2 if early_period == 0
// 分别对两个子样本进行回归

// 解释：
// 第一步生成了指示变量 `early_period` 来区分早期和晚期样本。
// 然后分别对两个子样本使用 `if` 条件进行回归。

// 运行结果：
// 得到两个子样本的回归结果，可以比较核心解释变量在不同时期的表现。

（四）增加控制变量

假设原本的模型只有自变量 x1 和 x2，现在增加控制变量 z1 和 z2。

reg y x1 x2 z1 z2
// 解释：
// 直接在回归命令中添加新的控制变量。

// 运行结果：
// 输出包含新增控制变量后的回归结果，观察核心解释变量系数的变化。

四、总结

通过以上几种常见的稳健性检验方法和 Stata 操作示例，我们可以对研究结果进行更全面和深入的评估。在实际应用中，应根据研究问题和数据特点选择合适的稳健性检验方法，并结合理论和实际情况对结果进行分析和解释。

本文里面主要介绍的有添加变量以及改变模型形式这种稳健性检验方法，除此之外，还包括

• 更换被解释变量

• 更换解释变量

• 排除共同机构投资者

• 考虑外部政策冲击

• 内生性分析

• 更换估计方法

• 样本的选择性偏差

• 更换研究样本

• 排除替代解释

稳健性检验还不会做？来看看这篇顶刊的7种稳健性检验方法 (qq.com)

稳健性检验与内生性问题 (qq.com)