[小样本图像分割]Hypercorrelation Squeeze for Few-Shot Segmenation

最新推荐文章于 2024-11-08 16:52:00 发布

XL_Dylan

最新推荐文章于 2024-11-08 16:52:00 发布

阅读量2.7k

点赞数 2

分类专栏：小样本医学图像分割文章标签：深度学习计算机视觉图像识别

本文链接：https://blog.csdn.net/qq_38932073/article/details/115749562

版权

小样本医学图像分割专栏收录该内容

7 篇文章

订阅专栏

本文介绍了一种名为HSNet的新型网络，利用多层次特征相关性和四维卷积在Few-Shot语义分割中解决对应关系难题。通过构建4D相关张量，网络能从不同层次捕获精细对应，同时通过高效权重稀疏化降低计算成本。实验表明，这种方法在有限监督下提高了分割精度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

用于Few-Shot分割的超关联压缩

论文地址
 开源代码

摘要

Few-Shot语义分割的目的是学习如何从查询图像中分割目标对象而只使用目标类的少量带注释的支持图像。这项具有挑战性的任务需要理解不同层次的视觉线索，并分析查询和支持图像之间的细粒度对应关系。为了解决这一问题，我们提出了利用多层次特征相关和高效四维卷积的超相关挤压网络(HSNet)。它从中间卷积层的不同层次中提取不同的特征，构建了一个4D相关张量集合，即超相关。该方法在金字塔结构中利用高效的中心四维卷积，以粗到细的方式逐步将高相关的高级语义和低级几何线索压缩到精确的分割掩码中。

存在的问题及解决方案

最近在语义对应方面的研究表明，利用密集的中间特征和利用高维卷积处理相关张量在建立准确对应方面是非常有效的。然而,尽管最近Few-Shot细分研究开始积极探索相关性学习(correlation learning)方向,他们中的大多数既没有利用从CNN的早期到晚期的不同层次的特征表示，也没有构建成对的特征关联来捕获细粒度的关联模式。有一些尝试利用具有多层特征的密集关联，但它们在某种意义上仍然有限，因为它们仅仅利用密集关联来获得图的注意力，仅使用一小部分中间的卷积层。

在这一工作中，我们将近期视觉对应研究中最具影响力的两种技术结合起来----多层次特征和四维卷积，并基于此设计一种新框架，成为超关联挤压网络HSNet（Hypercorrelation Squeeze Networks）。如图1所示，我们的网络利用来自许多不同中间CNN层的不同几何/语义特征表示来构建一个4D相关张量集合，即高相关性，它代表了在多个视觉方面的一组丰富的对应关系。同时为了减少大量使用高维卷积所带来的计算负担，我们通过合理的权重稀疏化设计了一个高效的4D核，该核能够实时推理，同时比现有的核更有效和轻量级。
在这里插入图片描述

方法

在这里插入图片描述

Hypercorrelation construction

在这里插入图片描述

给定一对查询-支持图像对 $I^{\mathrm{q}}, I^{\mathrm{s}} \in \mathbb{R}^{3 \times H \times W}$ ，骨干网产生 $L$ 对中间特征映射序列 $\left\{\left(\mathbf{F}_{l}^{\mathrm{q}}, \mathbf{F}_{l}^{\mathrm{s}}\right)\right\}_{l=1}^{L}$ ，然后使用支持掩码 $\mathbf{M}^{\mathbf{s}} \in\{0,1\}^{H \times W}$ 来mask每一个支持特征图 $\mathbf{F}_{l}^{\mathrm{s}} \in \mathbb{R}^{C_{l} \times H_{l} \times W_{l}}$ ,这么做的目的是通过放弃不相关的激活（因为mask是0，1二值的，所以这样可以将非目标区域置0）来获取更可靠的掩码预测：
在这里插入图片描述
其中 $\zeta _l$ 是插值函数，用于将mask和feature map置为相同大小，即 $\zeta_{l}: \mathbb{R}^{H \times W} \rightarrow \mathbb{R}^{C_{l} \times H_{l} \times W_{l}}$ 。对于后续的超相关构建，每一层的一对查询和掩码支持特征通过余弦相似构成一个4D相关张量 $\hat{\mathbf{C}}_{l} \in \mathbb{R}^{H_{l} \times W_{l} \times H_{l} \times W_{l}}$ ：
在这里插入图片描述
其中 $x^q$ 和 $x^s$ 分别表示特征图 $F^q_l$ 和 $\hat{F^s_l}$ 的二维空间位置，Relu则用于抑制噪声关联。从四维相关的结果集 $\left\{\hat{\mathbf{C}}_{l}\right\}_{l=1}^{L}$ ，我们收集具有相同空间大小的4D张量，并将其子集表示为 $\left\{\hat{\mathbf{C}}_{l}\right\}_{l \in \mathcal{L}_{p}}$ ，其中
$\mathcal{L}_{p}$ 表示FPN结构的CNN层索引 $\left\{ 1,...,L \right\}$ 中的第 $p$ 个金字塔层。最后，所有 $\left\{\hat{\mathbf{C}}_{l}\right\}_{l \in \mathcal{L}_{p}}$ 中的4D张量连接在一起构成超关联 $\mathbf{C}_{p} \in \mathbb{R}^{\left|\mathcal{L}_{p}\right| \times H_{p} \times W_{p} \times H_{p} \times W_{p}}$ ，其中 $H_p,W_p,H_p,W_p)$ 表示在金字塔层 $p$ 处的超关联空间分辨率。给定 $P$ 个金字塔层，我们称高相关金字塔为 $\mathcal{C}=\left\{\mathbf{C}_{p}\right\}_{p=1}^{P}$ ，表示来自多个视觉方面的丰富的特征关联集合。

4D-convolutional pyramid encoder

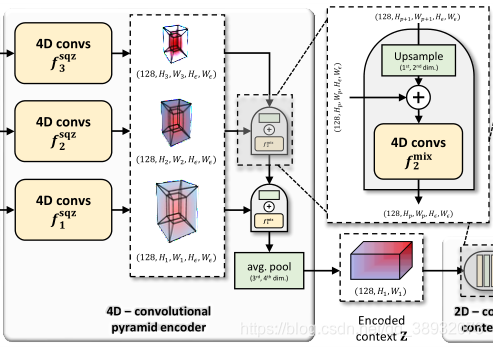
在这里插入图片描述

解码器网络将 $\mathcal{C}=\left\{\mathbf{C}_{p}\right\}_{p=1}^{P}$ 有效压缩成一个浓缩的特征图 $\mathbf{Z} \in \mathbb{R}^{128 \times H_{1} \times W_{1}}$ 。我们使用两种类型的构建块来实现这种相关性学习:压缩块 $f_p^{sqz}$ 和混合块 $f_p^{mix}$ 。每个区块包括三个序列的多通道4D卷积、组归一化（group norm）和ReLU激活，如图3所示。
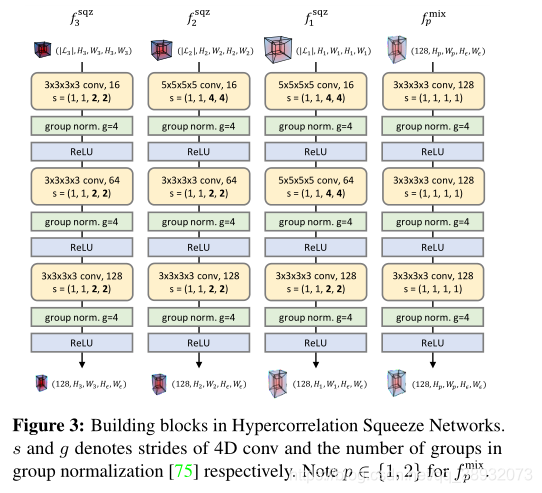
在这里插入图片描述
在 $f_p^{sqz}$ 中，大步长周期性地压缩 $C_p$ 的最后两个空间维度（支持表示）为 $\left(H_{\epsilon}, W_{\epsilon}\right)$ ，而前两个空间维度(查询表示)保持不变，例如 $f_{p}^{\mathrm{sqz}}: \mathbb{R}^{\left|\mathcal{L}_{p}\right| \times H_{p} \times W_{p} \times H_{p} \times W_{p}} \rightarrow \mathbb{R}^{128 \times H_{p} \times W_{p} \times H_{\epsilon} \times W_{\epsilon}}$ 。与FPN结构类似，相邻金字塔层的两个输出 $p$ 和 $p + 1$ 在对上层输出(查询)的空间维度上采样2倍后，通过元素相加的方式合并。也就是混合块可表示为： $f_{p}^{\mathrm{mix}}: \mathbb{R}^{{128} \times H_{p} \times W_{p} \times H_{\epsilon} \times W_{\epsilon}} \rightarrow \mathbb{R}^{128 \times H_{p} \times W_{p} \times H_{\epsilon} \times W_{\epsilon}}$ 。然后用四维卷积处理这一混合物，以自上而下的方式将相关信息传播到低层。在迭代传播之后，最底层混合块 $f_1^{mix}$ 的输出张量通过平均池化其最后两个(支持)空间维度进一步压缩，这反过来提供了一个二维的特征图 $\mathbf{Z} \in \mathbb{R}^{128 \times H_{1} \times W_{1}}$ ，这表示超相关 $C$ 的压缩表示。

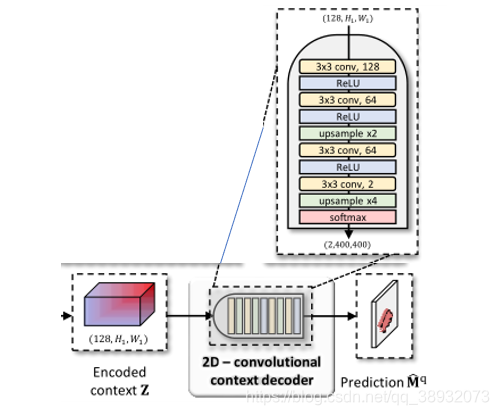
2D-convolutional context decoder

一个简单的二维解码器，如下图所示:
在这里插入图片描述

Center-pivot 4D convolution

显然，我们的网络具有如此大量的4D卷积，需要大量的资源。由于维度灾难问题，许多视觉对应方法只能使用少量的4D卷积层。为了解决这个问题，我们重新讨论了4D卷积操作，并深入研究了它的局限性。然后，我们演示了一个权重稀疏化方案来有效地解决这些问题。

论文在这一章节以及附录中使用公式详细推导了这一方案，有兴趣的可以去阅读原文，这里仅作概述：
在这里插入图片描述
虽然在相关张量上使用4D卷积在对应相关（correspondence-related）领域表现出了良好的经验性能，但其相对于输入特征大小的二次复杂度仍然是主要的瓶颈。另一个限制因素是高维核的过度参数化：考虑由nD卷积核卷积的nD张量中的单个激活。核处理这种激活的次数与n成指数比例。这意味着一些不可靠的大强度输入激活可能会在捕获可靠模式时带来一些噪声，这是由于它们过度暴露在高维核中的结果。

本文使用空间可分离的四维核来近似四维卷积，用两个单独的二维核以及额外的批处理归一化层来解决后一个问题(数值不稳定性)。

我们的目标是设计一个轻量级的4D内核，在内存和时间方面都是高效的，同时有效地接近现有的4D内核。我们通过合理的权重精简来实现这一点；从一个局部4D感兴趣窗口内的一组邻域位置出发，我们的内核旨在忽略位于4D窗口中相当不重要位置的大量激活，从而只关注相关激活的一小部分。具体来说，我们认为以二维中心之一(例如x或x’)为枢轴的位置上的激活是图4中最具影响力的位置。

实验结果

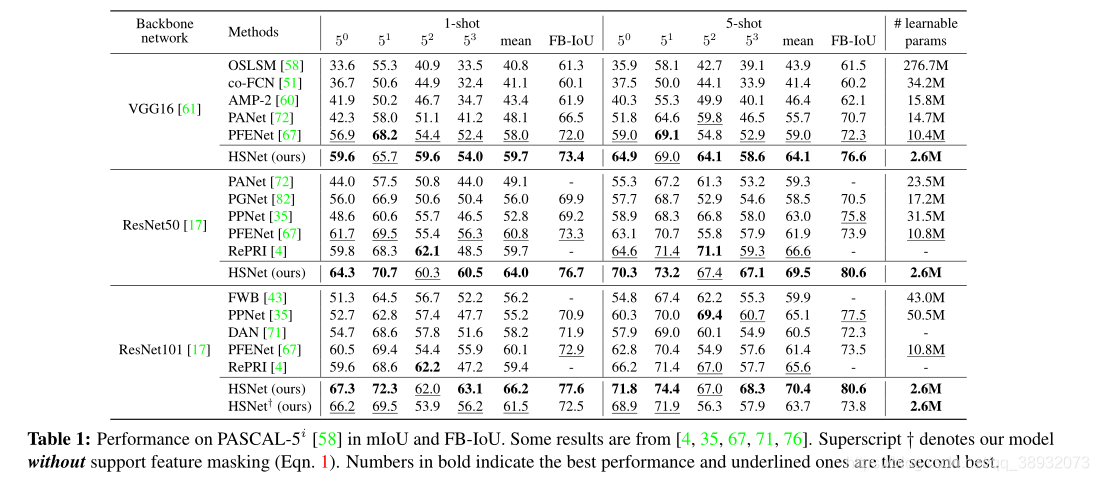
在这里插入图片描述

结论

我们提出了一种新的框架，使用轻量四维卷积以全卷积的方式分析复杂特征相关性。在三个标准基准上的性能显著提高表明，从多个视觉方面学习特征关系模式在有限监督下的细粒度分割是有效的。我们还演示了一种丢弃不重要权重的独特方法，它可以有效地将4D核分解为一对2D核，从而允许以非常小的成本广泛使用4D卷积层。我们相信，我们的研究将进一步促进4D卷积在其他需要学习分析高维相关性的领域的使用。