1.对任意时变力的响应
为分析单自由度体系随时间任意变化的力
F
(
t
)
F(t)
F(t)作用下的响应,发展了一般性的方法,能够解析地计算由时间的简单函数描述的力引起的响应。
m
u
¨
(
t
)
+
c
u
˙
(
t
)
+
k
u
(
t
)
=
F
(
t
)
m \ddot u(t)+c\dot u(t)+ku(t)=F(t)
mu¨(t)+cu˙(t)+ku(t)=F(t)
一个任意激振力可以看成是一系列脉冲激励的叠加,这样系统在任意激振力作用下的响应可以看成是由不同时刻脉冲激励作用下的脉冲响应的叠加。
1.1单位脉冲
工程上将单位脉冲定义为
δ
(
t
)
=
{
0
t
≠
0
∞
,
t
=
0
\delta(t)=\begin{cases} 0 & t \neq 0\\ \infty, & t=0 \end{cases}
δ(t)={0∞,t=0t=0
∫
−
∞
+
∞
δ
(
t
)
d
t
=
∫
0
−
0
+
δ
(
t
)
d
t
=
1
\int_{-\infty}^{+\infty}\delta(t)dt=\int_{0_{-}}^{0_{+}}\delta(t)dt=1
∫−∞+∞δ(t)dt=∫0−0+δ(t)dt=1
δ
\delta
δ函数具有如下性质:
δ
(
t
−
τ
)
=
{
0
t
≠
τ
∞
,
t
=
τ
\delta(t-\tau)=\begin{cases} 0 & t \neq \tau\\ \infty, & t=\tau \end{cases}
δ(t−τ)={0∞,t=τt=τ
∫
−
∞
+
∞
δ
(
t
)
d
t
=
1
\int_{-\infty}^{+\infty}\delta(t)dt=1
∫−∞+∞δ(t)dt=1
∫
−
∞
+
∞
δ
(
t
−
τ
)
f
(
t
)
d
t
=
f
(
τ
)
\int_{-\infty}^{+\infty}\delta(t-\tau)f(t)dt=f(\tau)
∫−∞+∞δ(t−τ)f(t)dt=f(τ)
若系统激励
f
(
t
)
f(t)
f(t)的作用时间非常短,可视为理想脉冲
δ
量纲:[时间]
−
1
\delta \text{量纲:[时间]}^{-1}
δ量纲:[时间]−1
F
(
t
)
=
I
δ
(
t
)
F(t)=I\delta (t)
F(t)=Iδ(t)
当
f
(
t
)
f(t)
f(t)代表力时,则表示一次锤击或一个脉冲冲量,
I
I
I具有力乘时间的量纲。
“冲量”一词原只用于力冲量,在此进行扩展,可以代表任意一种输入参量,随代表的物理量不同, I I I的量纲也不同。
如当 F ( t ) F(t) F(t)代表加速度时, I I I的量纲为加速度×时间。
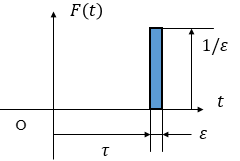
矩形脉冲如图所示:宽度为
ε
\varepsilon
ε,高度为
1
/
ε
1/\varepsilon
1/ε,面积为1。随着
ε
\varepsilon
ε趋于零,力趋于无穷大,然而,由
F
(
t
)
F(t)
F(t)的时间积分定义的脉冲幅值仍等于1。
::: hljs-center
:::
ε → 0 \varepsilon\rightarrow0 ε→0时的力称为单位脉冲。
D i r a c − δ Dirac-\delta Dirac−δ函数 δ ( t − τ ) \delta(t-\tau) δ(t−τ)在数学上定义为以 t = τ t=\tau t=τ为中心的单位脉冲。
注意:如果矩形面积 = E =E =E,冲激强度为 E E E。
1.2对单位脉冲的响应
系统在单位脉冲激励下的振动微分方程为
m
u
¨
(
t
)
+
c
u
˙
(
t
)
+
k
u
(
t
)
=
δ
(
t
)
m \ddot u(t)+c\dot u(t)+ku(t)=\delta(t)
mu¨(t)+cu˙(t)+ku(t)=δ(t)
方程的位移响应就是脉冲响应函数。将上式中各项乘以
d
t
dt
dt并进行简单的整理,得到如下形式:
m
d
u
˙
(
t
)
+
c
d
u
(
t
)
+
k
u
d
t
=
δ
(
t
)
d
t
m d\dot u(t)+cd u(t)+kudt=\delta(t)dt
mdu˙(t)+cdu(t)+kudt=δ(t)dt
两种初始条件:
(1)当时,系统是静止的,即初速度和位移皆为零
u
(
0
−
)
=
u
˙
(
0
−
)
=
0
u(0_{-})=\dot u(0_{-})=0
u(0−)=u˙(0−)=0
(2)在的邻域内,单位脉冲力
δ
(
t
)
\delta(t)
δ(t)作用瞬间由于作用时间等于零,位移来不及变化,但速度可以发生突变,这样上式中
u
=
0
,
d
u
=
0
u=0,du=0
u=0,du=0,,因此有
m
d
u
˙
=
δ
(
t
)
d
t
md\dot u=\delta(t)dt
mdu˙=δ(t)dt
将上式进行积分,得到速度的增量
1
/
m
1/m
1/m,上式也就是冲量定理。脉冲载荷作用结束后后,系统的位移和速度分别为
u
(
0
)
=
0
,
u
˙
(
0
)
=
1
/
m
u(0)=0,\dot u(0)=1/m
u(0)=0,u˙(0)=1/m
当
t
>
0
t>0
t>0时,,上式变为
m
u
¨
(
t
)
+
c
u
˙
(
t
)
+
k
u
(
t
)
=
0
m \ddot u(t)+c\dot u(t)+ku(t)=0
mu¨(t)+cu˙(t)+ku(t)=0
这就是弹簧-质量系统的有阻尼自由振动微分方程。表示衰减振动,在小阻尼情况下,其通解为
u
(
t
)
=
e
ξ
w
n
t
(
A
cos
w
d
t
+
B
sin
w
d
t
)
u(t)=e^{\xi w_nt}(A\cos w_dt+B\sin w_dt)
u(t)=eξwnt(Acoswdt+Bsinwdt)
根据初始条件,可以确定其中的待定系数,因此有
h
(
t
)
=
u
(
t
)
=
1
m
w
n
1
−
ξ
2
e
−
ξ
w
n
t
sin
[
w
n
1
−
ξ
2
t
]
(
t
≥
0
)
h(t)=u(t)=\frac{1}{mw_n\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin [w_n\sqrt{1-\xi^2}t](t\geq 0)
h(t)=u(t)=mwn1−ξ21e−ξwntsin[wn1−ξ2t](t≥0)
当开始时间
t
=
τ
t=\tau
t=τ时
h
(
t
−
τ
)
=
u
(
t
)
=
1
m
w
n
1
−
ξ
2
e
−
ξ
w
n
(
t
−
τ
)
sin
[
w
n
1
−
ξ
2
(
t
−
τ
)
]
(
t
≥
τ
)
h(t-\tau)=u(t)=\frac{1}{mw_n\sqrt{1-\xi^2}}e^{-\xi w_n(t-\tau)}\sin [w_n\sqrt{1-\xi^2}(t-\tau)](t\geq\tau)
h(t−τ)=u(t)=mwn1−ξ21e−ξwn(t−τ)sin[wn1−ξ2(t−τ)](t≥τ)
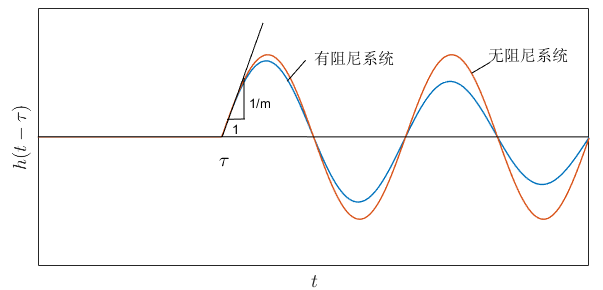
用
h
(
t
−
τ
)
h(t-\tau)
h(t−τ)表示这个单位脉冲反应函数,示与下图。
::: hljs-center
:::
由上式给出的暂态响应也相当于系统在
t
=
τ
t=\tau
t=τ时刻受单位冲量作用而产生的响应。
I
0
=
lim
ε
→
0
∫
τ
−
ε
τ
+
ε
δ
(
t
−
τ
)
d
t
=
1
I_0=\lim_{\varepsilon\rightarrow0}\int_{\tau-\varepsilon}^{\tau+\varepsilon}\delta(t-\tau)dt=1
I0=ε→0lim∫τ−ετ+εδ(t−τ)dt=1
那么系统在
t
=
τ
t=\tau
t=τ时刻受任意冲量
I
I
I作用而产生的响应可以用脉冲响应函数表示为
u
(
t
)
=
I
×
h
(
t
−
τ
)
u(t)=I\times h(t-\tau)
u(t)=I×h(t−τ)
如果激励是单位脉冲地面运动,有
F
e
f
f
(
t
)
=
−
m
δ
(
t
−
τ
)
F_{eff}(t)=-m\delta(t-\tau)
Feff(t)=−mδ(t−τ),则初始条件变为
u
˙
(
t
)
=
−
1
,
u
(
τ
)
=
0
\dot u(t)=-1,u(\tau)=0
u˙(t)=−1,u(τ)=0
可得粘性阻尼系统的响应方程为
h
(
t
−
τ
)
=
u
(
t
)
=
−
1
w
n
1
−
ξ
2
e
−
ξ
w
n
(
t
−
τ
)
sin
[
w
n
1
−
ξ
2
(
t
−
τ
)
]
(
t
≥
τ
)
h(t-\tau)=u(t)=-\frac{1}{w_n\sqrt{1-\xi^2}}e^{-\xi w_n(t-\tau)}\sin [w_n\sqrt{1-\xi^2}(t-\tau)](t\geq\tau)
h(t−τ)=u(t)=−wn1−ξ21e−ξwn(t−τ)sin[wn1−ξ2(t−τ)](t≥τ)
1.3对任意激励的响应
一个随时间任意变化的力
F
(
t
)
F(t)
F(t)可以描绘成无穷小短脉冲的序列,如下图所示。线性动力体系对这些脉冲的一个
τ
\tau
τ时刻,大小为
F
(
τ
)
d
τ
F(\tau)d\tau
F(τ)dτ的脉冲响应,时单位脉冲函数的
F
(
τ
)
d
τ
F(\tau)d\tau
F(τ)dτ倍
d
u
(
t
)
=
[
F
(
τ
)
d
τ
]
h
(
t
−
τ
)
du(t)=[F(\tau)d\tau]h(t-\tau)
du(t)=[F(τ)dτ]h(t−τ)
系统在时刻
t
t
t的响应为直到该时刻所有脉冲响应之和
u
(
t
)
=
∫
0
t
F
(
τ
)
h
(
t
−
τ
)
d
τ
u(t)=\int _0^tF(\tau)h(t-\tau)d\tau
u(t)=∫0tF(τ)h(t−τ)dτ
上式称为卷积积分,应用于任意线性动力方程的一般解。
::: hljs-center
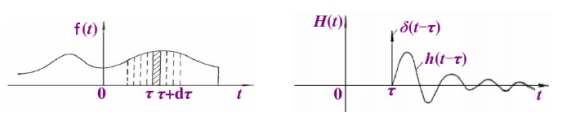
:::
将单位脉冲响应函数代入上式,得Duhamel积分
u
(
t
)
=
1
m
w
n
1
−
ξ
2
∫
0
t
F
(
τ
)
e
−
ξ
w
n
(
t
−
τ
)
sin
[
w
n
1
−
ξ
2
(
t
−
τ
)
]
d
τ
u(t)=\frac{1}{mw_n\sqrt{1-\xi^2}}\int _0^tF(\tau)e^{-\xi w_n(t-\tau)}\sin [w_n\sqrt{1-\xi^2}(t-\tau)]d\tau
u(t)=mwn1−ξ21∫0tF(τ)e−ξwn(t−τ)sin[wn1−ξ2(t−τ)]dτ
无阻尼体系,简化为
u
(
t
)
=
1
m
w
n
∫
0
t
F
(
τ
)
sin
[
w
n
(
t
−
τ
)
]
d
τ
u(t)=\frac{1}{mw_n}\int _0^tF(\tau)\sin [w_n(t-\tau)]d\tau
u(t)=mwn1∫0tF(τ)sin[wn(t−τ)]dτ
这个结果的初始条件为“静止”,即
u
(
0
)
=
u
˙
(
0
)
=
0
u(0)=\dot u(0)=0
u(0)=u˙(0)=0。如果初位移和速度分别为
u
(
0
)
u(0)
u(0)和
u
˙
(
0
)
\dot u(0)
u˙(0),则上式需要将加上下式由初始条件引起的自由振动。
u
(
t
)
=
u
(
0
)
cos
ω
n
t
+
u
˙
(
0
)
ω
n
sin
ω
n
t
+
1
m
w
n
1
−
ξ
2
∫
0
t
F
(
τ
)
e
−
ξ
w
n
(
t
−
τ
)
sin
[
w
n
1
−
ξ
2
(
t
−
τ
)
]
d
τ
u(t)=u(0)\cos\omega_nt+\frac{\dot u(0)}{\omega_n}\sin\omega_nt+\frac{1}{mw_n\sqrt{1-\xi^2}}\int _0^tF(\tau)e^{-\xi w_n(t-\tau)}\sin [w_n\sqrt{1-\xi^2}(t-\tau)]d\tau
u(t)=u(0)cosωnt+ωnu˙(0)sinωnt+mwn1−ξ21∫0tF(τ)e−ξwn(t−τ)sin[wn1−ξ2(t−τ)]dτ
u
(
t
)
=
e
−
ξ
ω
n
t
(
u
0
cos
ω
d
t
+
u
˙
0
+
ξ
ω
n
u
0
ω
d
sin
ω
d
t
)
+
1
m
w
n
1
−
ξ
2
∫
0
t
F
(
τ
)
e
−
ξ
w
n
(
t
−
τ
)
sin
[
w
n
1
−
ξ
2
(
t
−
τ
)
]
d
τ
u(t)=e^{-\xi\omega_nt}(u_0\cos\omega_dt+\frac{\dot u_0+\xi\omega_nu_0}{\omega_d}\sin\omega_dt)+\frac{1}{mw_n\sqrt{1-\xi^2}}\int _0^tF(\tau)e^{-\xi w_n(t-\tau)}\sin [w_n\sqrt{1-\xi^2}(t-\tau)]d\tau
u(t)=e−ξωnt(u0cosωdt+ωdu˙0+ξωnu0sinωdt)+mwn1−ξ21∫0tF(τ)e−ξwn(t−τ)sin[wn1−ξ2(t−τ)]dτ
2. 脉冲响应的规范化
激励是力定义的,则规范化方程为
z ¨ ( t ) + 2 ξ ω n z ˙ ( t ) + ω n 2 z ( t ) = ω n 2 F ( t ) k \ddot{z}(t)+2\xi\omega_n\dot{z}(t)+\omega_n^2z(t)=\omega_n^2\frac{F(t)}{k} z¨(t)+2ξωnz˙(t)+ωn2z(t)=ωn2kF(t)
激励是加速度定义的,则规范化方程为
z ¨ ( t ) + 2 ξ ω n z ˙ ( t ) + ω n 2 z ( t ) = ω n 2 ( − x ¨ w n 2 ) \ddot{z}(t)+2\xi\omega_n\dot{z}(t)+\omega_n^2z(t)=\omega_n^2(-\frac{\ddot x}{w_n^2}) z¨(t)+2ξωnz˙(t)+ωn2z(t)=ωn2(−wn2x¨)
2.1相对位移定义的响应
激励是力定义的,则可得
z
¨
(
t
)
+
2
ξ
ω
n
z
˙
(
t
)
+
ω
n
2
z
(
t
)
=
ω
n
2
δ
F
(
t
)
k
\ddot{z}(t)+2\xi\omega_n\dot{z}(t)+\omega_n^2z(t)=\omega_n^2\frac{\delta_F(t)}{k}
z¨(t)+2ξωnz˙(t)+ωn2z(t)=ωn2kδF(t)
式中,
δ
F
=
F
δ
(
t
)
\delta_F=F\delta(t)
δF=Fδ(t),
F
=
1
F=1
F=1(力),
δ
\delta
δ为狄拉克函数。
激励是加速度定义的,则可得
z
¨
(
t
)
+
2
ξ
ω
n
z
˙
(
t
)
+
ω
n
2
z
(
t
)
=
ω
n
2
(
−
δ
A
C
(
t
)
w
n
2
)
\ddot{z}(t)+2\xi\omega_n\dot{z}(t)+\omega_n^2z(t)=\omega_n^2(-\frac{\delta_{AC}(t)}{w_n^2})
z¨(t)+2ξωnz˙(t)+ωn2z(t)=ωn2(−wn2δAC(t))
式中,
δ
A
C
(
t
)
=
x
¨
δ
(
t
)
\delta_{AC}(t)=\ddot x\delta(t)
δAC(t)=x¨δ(t),
x
¨
=
1
\ddot x=1
x¨=1(加速度),
δ
\delta
δ为狄拉克函数。
如果
δ
g
(
t
)
\delta_g(t)
δg(t)为规范化的脉冲函数,根据不同情况分别等于
δ
F
(
t
)
k
\frac{\delta_F(t)}{k}
kδF(t),
−
δ
A
C
(
t
)
w
n
2
-\frac{\delta_{AC}(t)}{w_n^2}
−wn2δAC(t),那么得到下列规范化的公式
u
¨
(
t
)
+
2
ξ
ω
n
u
˙
(
t
)
+
ω
n
2
u
(
t
)
=
ω
n
2
δ
g
(
t
)
\ddot{u}(t)+2\xi\omega_n\dot{u}(t)+\omega_n^2u(t)=\omega_n^2\delta_{g}(t)
u¨(t)+2ξωnu˙(t)+ωn2u(t)=ωn2δg(t)
那么
L
=
∫
0
Δ
t
δ
g
(
t
)
d
t
=
{
∫
0
Δ
t
δ
F
(
t
)
k
d
t
=
1
k
I
∫
0
Δ
t
−
δ
A
C
(
t
)
w
n
2
d
t
=
−
1
w
n
2
I
=
−
δ
V
w
n
2
L=\int^{\Delta t}_0\delta_g(t)dt=\begin{cases} \int^{\Delta t}_0\frac{\delta_F(t)}{k}dt=\frac{1}{k}I \\ \int^{\Delta t}_0-\frac{\delta_{AC}(t)}{w_n^2}dt=-\frac{1}{w_n^2}I=-\frac{\delta V}{w_n^2} \end{cases}
L=∫0Δtδg(t)dt={∫0ΔtkδF(t)dt=k1I∫0Δt−wn2δAC(t)dt=−wn21I=−wn2δV
式中,
δ
V
\delta V
δV为由加速度脉冲引起的速度变化。
为了使微分方程变成无量纲,每个分量都除以
L
w
n
Lw_n
Lwn(量纲为长度)
u
¨
(
t
)
L
w
n
+
2
ξ
ω
n
u
˙
(
t
)
L
w
n
+
ω
n
2
u
(
t
)
L
w
n
=
ω
n
2
δ
g
(
t
)
L
w
n
\frac{\ddot{u}(t)}{Lw_n}+2\xi \omega _n\frac{\dot{u}(t)}{Lw_n}+\omega_n^2\frac{{u}(t)}{Lw_n}=\omega_n^2\frac{\delta_g(t)}{Lw_n}
Lwnu¨(t)+2ξωnLwnu˙(t)+ωn2Lwnu(t)=ωn2Lwnδg(t)
设
q
=
u
/
(
L
w
n
)
q=u/(Lw_n)
q=u/(Lwn)和
θ
=
w
0
t
\theta=w_0t
θ=w0t,则方程变为
q
¨
(
t
)
+
2
ξ
ω
n
q
˙
(
t
)
+
ω
n
2
q
(
t
)
=
ω
n
2
δ
g
(
t
)
L
w
n
\ddot q(t)+2\xi \omega _n\dot q(t)+\omega_n^2q(t)=\omega_n^2\frac{\delta_g(t)}{Lw_n}
q¨(t)+2ξωnq˙(t)+ωn2q(t)=ωn2Lwnδg(t)
且
θ
=
ω
n
t
\theta=\omega_nt
θ=ωnt
则
d
q
d
t
=
d
q
d
θ
d
θ
d
t
=
ω
n
d
q
d
θ
\frac{dq}{dt}=\frac{dq}{d\theta}\frac{d\theta}{dt}=\omega_n\frac{dq}{d\theta}
dtdq=dθdqdtdθ=ωndθdq
d
2
q
d
t
2
=
d
2
q
d
θ
2
(
d
θ
d
t
)
2
=
ω
n
2
d
2
q
d
θ
2
\frac{d^2q}{dt^2}=\frac{d^2q}{d\theta^2}(\frac{d\theta}{dt})^2=\omega_n^2\frac{d^2q}{d\theta^2}
dt2d2q=dθ2d2q(dtdθ)2=ωn2dθ2d2q
可得力激励和加速度激励简化方程:
q ¨ ( θ ) + 2 ξ ω n q ˙ ( θ ) + ω n 2 q ( θ ) = δ g ( t ) L w n \ddot{q}(\theta)+2\xi\omega_n\dot{q}(\theta)+\omega_n^2q(\theta)=\frac{\delta_g(t)}{Lw_n} q¨(θ)+2ξωnq˙(θ)+ωn2q(θ)=Lwnδg(t)
狄拉克函数
δ
(
θ
)
\delta(\theta)
δ(θ)服从下列要求
{
δ
g
(
θ
)
=
0
(
θ
≠
0
)
δ
g
(
0
)
=
∞
∫
−
∞
+
∞
δ
g
(
θ
)
d
t
=
1
\begin{cases} \delta_g(\theta)=0 (\theta \neq 0)\\ \delta_g(0)=\infty\\ \int^{+\infty}_{-\infty}\delta_g(\theta)dt=1 \end{cases}
⎩
⎨
⎧δg(θ)=0(θ=0)δg(0)=∞∫−∞+∞δg(θ)dt=1
即
θ
=
0
\theta=0
θ=0,
q
=
0
q=0
q=0,
m
d
q
d
t
=
1
m\frac{dq}{dt}=1
mdtdq=1。
{ δ g ( θ ) = 0 ( θ ≠ 0 ) δ g ( 0 ) = ∞ ∫ − ∞ + ∞ δ g ( θ ) d θ w n = 1 w n ∫ − ∞ + ∞ δ g ( θ ) d θ = 1 \begin{cases} \delta_g(\theta)=0 (\theta \neq 0)\\ \delta_g(0)=\infty\\ \int^{+\infty}_{-\infty}\delta_g(\theta)d\frac{\theta}{w_n}=\frac{1}{w_n}\int^{+\infty}_{-\infty}\delta_g(\theta)d\theta=1 \end{cases} ⎩ ⎨ ⎧δg(θ)=0(θ=0)δg(0)=∞∫−∞+∞δg(θ)dwnθ=wn1∫−∞+∞δg(θ)dθ=1
则方程变为
q ¨ ( θ ) + 2 ξ ω n q ˙ ( θ ) + ω n 2 q ( θ ) = δ g ( θ ) \ddot{q}(\theta)+2\xi\omega_n\dot{q}(\theta)+\omega_n^2q(\theta)=\delta_g(\theta) q¨(θ)+2ξωnq˙(θ)+ωn2q(θ)=δg(θ)
此方程的拉氏变换为
Q ( p ) ( P 2 + 2 ξ p + 1 ) = 1 Q(p)(P^2+2\xi p+1)=1 Q(p)(P2+2ξp+1)=1
Q ( p ) = 1 P 2 + 2 ξ p + 1 Q(p)=\frac{1}{P^2+2\xi p+1} Q(p)=P2+2ξp+11
引入脉冲响应函数 h ( θ ) h(\theta) h(θ)
q ( θ ) = 1 1 − ξ 2 e − ξ θ sin ( θ 1 − ξ 2 ) = h ( θ ) ( ξ ≠ 1 ) q(\theta)=\frac{1}{\sqrt{1-\xi^2}}e^{-\xi \theta}\sin (\theta\sqrt{1-\xi^2})=h(\theta)(\xi\neq 1) q(θ)=1−ξ21e−ξθsin(θ1−ξ2)=h(θ)(ξ=1)
则
u ( t ) = w n L 1 1 − ξ 2 e − ξ w n t sin ( w n t 1 − ξ 2 ) u(t)=w_nL\frac{1}{\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin (w_nt\sqrt{1-\xi^2}) u(t)=wnL1−ξ21e−ξwntsin(wnt1−ξ2)
对于加速度狄拉克函数,有
u ( t ) = − δ V w n 1 1 − ξ 2 e − ξ w n t sin ( w n t 1 − ξ 2 ) u(t)=-\frac{\delta V}{w_n}\frac{1}{\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin (w_nt\sqrt{1-\xi^2}) u(t)=−wnδV1−ξ21e−ξwntsin(wnt1−ξ2)
和
w n 2 u ( t ) = − w n δ V 1 1 − ξ 2 e − ξ w n t sin ( w n t 1 − ξ 2 ) w_n^2u(t)=-w_n\delta V\frac{1}{\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin (w_nt\sqrt{1-\xi^2}) wn2u(t)=−wnδV1−ξ21e−ξwntsin(wnt1−ξ2)
如果
L
=
1
L=1
L=1,则有
h
(
t
)
=
w
n
1
1
−
ξ
2
e
−
ξ
w
n
t
sin
(
w
n
t
1
−
ξ
2
)
(
t
≥
0
)
\color{red}h(t)=w_n\frac{1}{\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin (w_nt\sqrt{1-\xi^2})(t\geq 0)
h(t)=wn1−ξ21e−ξwntsin(wnt1−ξ2)(t≥0)
如果脉冲用力定义,
L
=
1
/
k
L=1/k
L=1/k,则
u
(
t
)
=
w
n
k
1
1
−
ξ
2
e
−
ξ
w
n
t
sin
(
w
n
t
1
−
ξ
2
)
u(t)=\frac{w_n}{k}\frac{1}{\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin (w_nt\sqrt{1-\xi^2})
u(t)=kwn1−ξ21e−ξwntsin(wnt1−ξ2)
=
1
m
k
1
1
−
ξ
2
e
−
ξ
w
n
t
sin
(
w
n
t
1
−
ξ
2
)
=\frac{1}{\sqrt{mk}}\frac{1}{\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin (w_nt\sqrt{1-\xi^2})
=mk11−ξ21e−ξwntsin(wnt1−ξ2)
其中
L
=
∫
0
Δ
t
δ
F
(
t
)
k
d
t
=
∫
0
Δ
t
F
δ
(
t
)
k
d
t
=
F
k
∫
0
Δ
t
δ
(
t
)
d
t
=
1
/
k
L=\int^{\Delta t}_0\frac{\delta_F(t)}{k}dt=\int^{\Delta t}_0\frac{F\delta(t)}{k}dt=\frac{F}{k}\int^{\Delta t}_0\delta(t)dt=1/k
L=∫0ΔtkδF(t)dt=∫0ΔtkFδ(t)dt=kF∫0Δtδ(t)dt=1/k
因
F
=
1
F=1
F=1,得
∫
0
Δ
t
δ
(
t
)
d
t
=
1
\int^{\Delta t}_0\delta(t)dt=1
∫0Δtδ(t)dt=1
由1.2节可知方程
z
¨
(
t
)
+
2
ξ
ω
n
z
˙
(
t
)
+
ω
n
2
z
(
t
)
=
ω
n
2
F
(
t
)
k
=
ω
n
2
δ
(
t
)
k
\ddot{z}(t)+2\xi\omega_n\dot{z}(t)+\omega_n^2z(t)=\omega_n^2\frac{F(t)}{k}=\omega_n^2\frac{\delta(t)}{k}
z¨(t)+2ξωnz˙(t)+ωn2z(t)=ωn2kF(t)=ωn2kδ(t)的脉冲响应函数为
u
(
t
)
=
1
m
w
n
1
−
ξ
2
e
−
ξ
w
n
t
sin
[
w
n
1
−
ξ
2
t
]
u(t)=\frac{1}{mw_n\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin [w_n\sqrt{1-\xi^2}t]
u(t)=mwn1−ξ21e−ξwntsin[wn1−ξ2t]
u
(
t
)
=
1
m
k
1
−
ξ
2
e
−
ξ
w
n
t
sin
[
w
n
1
−
ξ
2
t
]
u(t)=\frac{1}{\sqrt{mk}\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin [w_n\sqrt{1-\xi^2}t]
u(t)=mk1−ξ21e−ξwntsin[wn1−ξ2t]
式左右的量纲是一致的,数值“1”对应着脉冲
1
k
m
=
I
k
m
\frac{1}{\sqrt{km}}=\frac{I}{\sqrt{km}}
km1=kmI,其量纲是位移。因
L
=
1
/
k
L=1/k
L=1/k,可知脉冲
I
I
I的单位
N
⋅
s
N\cdot s
N⋅s,即
N
⋅
s
N
/
m
⋅
k
g
=
N
⋅
s
k
g
⋅
m
/
s
2
/
m
⋅
k
g
=
k
g
⋅
m
/
s
2
⋅
s
k
g
/
s
=
m
\frac{N\cdot s}{\sqrt{N/m\cdot kg}}=\frac{N\cdot s}{\sqrt{kg\cdot m/s^2/m\cdot kg}}=\frac{kg\cdot m/s^2\cdot s}{kg/s}=m
N/m⋅kgN⋅s=kg⋅m/s2/m⋅kgN⋅s=kg/skg⋅m/s2⋅s=m
当
L
=
F
/
k
L=F/k
L=F/k,得
∫
0
Δ
t
δ
(
t
)
d
t
=
F
\int^{\Delta t}_0\delta(t)dt=F
∫0Δtδ(t)dt=F
由1.2节可知方程
z
¨
(
t
)
+
2
ξ
ω
n
z
˙
(
t
)
+
ω
n
2
z
(
t
)
=
ω
n
2
F
(
t
)
k
=
ω
n
2
δ
(
t
)
k
\ddot{z}(t)+2\xi\omega_n\dot{z}(t)+\omega_n^2z(t)=\omega_n^2\frac{F(t)}{k}=\omega_n^2\frac{\delta(t)}{k}
z¨(t)+2ξωnz˙(t)+ωn2z(t)=ωn2kF(t)=ωn2kδ(t)的脉冲响应函数为
u
(
t
)
=
F
m
w
n
1
−
ξ
2
e
−
ξ
w
n
t
sin
[
w
n
1
−
ξ
2
t
]
u(t)=\frac{F}{mw_n\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin [w_n\sqrt{1-\xi^2}t]
u(t)=mwn1−ξ2Fe−ξwntsin[wn1−ξ2t]
u
(
t
)
=
F
m
k
1
−
ξ
2
e
−
ξ
w
n
t
sin
[
w
n
1
−
ξ
2
t
]
u(t)=\frac{F}{\sqrt{mk}\sqrt{1-\xi^2}}e^{-\xi w_nt}\sin [w_n\sqrt{1-\xi^2}t]
u(t)=mk1−ξ2Fe−ξwntsin[wn1−ξ2t]
式左右的量纲是一致的,数值“1”对应着脉冲
F
k
m
=
F
I
k
m
\frac{F}{\sqrt{km}}=\frac{FI}{\sqrt{km}}
kmF=kmFI,其量纲是位移。因
L
=
F
/
k
L=F/k
L=F/k,可知脉冲
I
I
I的单位
s
s
s,即
N
⋅
s
N
/
m
⋅
k
g
=
N
⋅
s
k
g
⋅
m
/
s
2
/
m
⋅
k
g
=
k
g
⋅
m
/
s
2
⋅
s
k
g
/
s
=
m
\frac{N\cdot s}{\sqrt{N/m\cdot kg}}=\frac{N\cdot s}{\sqrt{kg\cdot m/s^2/m\cdot kg}}=\frac{kg\cdot m/s^2\cdot s}{kg/s}=m
N/m⋅kgN⋅s=kg⋅m/s2/m⋅kgN⋅s=kg/skg⋅m/s2⋅s=m
2.2用绝对参数定义的响应
响应的拉氏表达式
Q
(
p
)
=
1
+
2
ξ
p
p
2
+
2
ξ
p
+
1
Q(p)=\frac{1+2\xi p}{p^2+2\xi p+1}
Q(p)=p2+2ξp+11+2ξp
q
(
θ
)
=
h
(
θ
)
=
e
−
ξ
θ
[
2
ξ
cos
(
1
−
ξ
2
θ
)
+
1
−
2
ξ
2
1
−
x
i
2
sin
1
−
ξ
2
θ
]
q(\theta)=h(\theta)=e^{-\xi\theta }[2\xi\cos (\sqrt{1-\xi^2}\theta)+\frac{1-2\xi^2}{\sqrt{1-xi^2}}\sin \sqrt{1-\xi^2}\theta]
q(θ)=h(θ)=e−ξθ[2ξcos(1−ξ2θ)+1−xi21−2ξ2sin1−ξ2θ]
即
h
(
θ
)
=
e
−
ξ
θ
1
−
ξ
2
sin
(
1
−
ξ
2
θ
+
ϕ
)
h(\theta)=\frac{ e^{-\xi\theta }}{\sqrt{1-\xi^2}}\sin (\sqrt{1-\xi^2}\theta+\phi)
h(θ)=1−ξ2e−ξθsin(1−ξ2θ+ϕ)
tan
ϕ
=
2
ξ
1
−
x
i
2
1
−
2
ξ
2
\tan \phi=\frac{2\xi\sqrt{1-xi^2}}{1-2\xi^2}
tanϕ=1−2ξ22ξ1−xi2
在未简化坐标系下,脉冲响应可以表示为
u
(
t
)
=
w
n
L
e
−
ξ
(
1
−
ξ
2
w
n
t
[
2
ξ
cos
w
n
t
)
+
1
−
2
ξ
2
1
−
x
i
2
sin
1
−
ξ
2
w
n
t
]
u(t)=w_nLe^{-\xi (\sqrt{1-\xi^2}w_nt}[2\xi\cos w_nt)+\frac{1-2\xi^2}{\sqrt{1-xi^2}}\sin \sqrt{1-\xi^2}w_nt]
u(t)=wnLe−ξ(1−ξ2wnt[2ξcoswnt)+1−xi21−2ξ2sin1−ξ2wnt]
若
L
=
1
L=1
L=1,则有
h
(
t
)
=
w
n
e
−
ξ
w
n
t
[
2
ξ
cos
(
1
−
ξ
2
w
n
t
)
+
1
−
2
ξ
2
1
−
x
i
2
sin
1
−
ξ
2
w
n
t
]
\color{red}h(t)=w_ne^{-\xi w_nt}[2\xi \cos (\sqrt{1-\xi^2}w_nt)+\frac{1-2\xi^2}{\sqrt{1-xi^2}}\sin \sqrt{1-\xi^2}w_nt]
h(t)=wne−ξwnt[2ξcos(1−ξ2wnt)+1−xi21−2ξ2sin1−ξ2wnt]
两个函数
l
l
l和
H
H
H的卷积的傅里叶变换等于它们傅里叶变换的积。如果
u
=
l
∗
h
u=l*h
u=l∗h,则有
U
(
Ω
)
=
F
T
(
U
)
=
F
T
(
l
∗
h
)
=
L
(
Ω
)
⋅
H
(
Ω
)
U(\Omega)=FT(U)=FT(l*h)=L(\Omega)\cdot H(\Omega)
U(Ω)=FT(U)=FT(l∗h)=L(Ω)⋅H(Ω)
脉冲响应的傅里叶变换函数
H
(
Ω
)
H(\Omega)
H(Ω)就是系统的传递函数。
线性单自由度微分方程的拉普拉斯变换有相似的关系
U
(
p
)
=
A
(
p
)
L
(
p
)
U(p)=A(p)L(p)
U(p)=A(p)L(p)
式中,
A
(
p
)
A(p)
A(p)为导纳,
Z
(
p
)
=
1
/
A
(
p
)
Z(p)=1/A(p)
Z(p)=1/A(p)为系统广义阻抗。
参考:Anil K. Chopra. 结构动力学理论及其在地震工程中应用[M].北京:高等教育出版社,2016.




















 820
820

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








