GAN原理解析，公式推导与python实现

1-生成模型

---

1-1 生成模型与判别模型

生成式对抗网络，顾名思义就是生成模型嘛！那什么是生成模型呢？与判别模型有什么区别呢？

先来理解一下判别模型。
学过机器学习的人都知道，入门级的算法逻辑回归，最后的预测，是通过sigmoid函数：

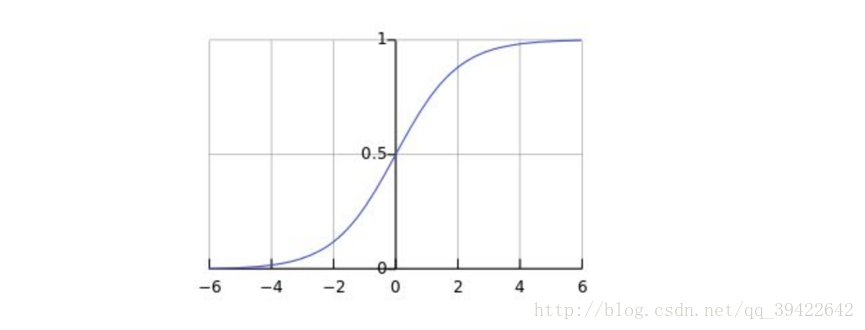
生成一个0-1之间的数值，然后用某一阀值来做分类，我们称之为判别模型：由数据直接学习，通过决策函数$Y = f(X)$或者概率模型$P(Y|X)$预测,判断类别的模型。逻辑回归中的sigmoid函数就是判别函数。

而生成模型，则先学习出一个联合概率密度分布$P(X,Y)$,最后分类，预测的时候，使用条件概率公式

$$P(Y|X) = \frac{P(X,Y)}{P(X)}$$ 来预测当前样本属于每一类的概率。
生成模型的核心，就是先求两个比较好求的概率，然后通过贝叶斯概率公式这样的关系来进行分类。

简单的看，

1-2 为什么学习生成模型？

我们可以总结一下它的优点：

1. 能生成高维的数据或者复杂的概率分布，且高维数据分布在数学和工业界都扮演着重要的作用
2. 还可以为强化学习做一定准备
3. 对于缺失数据较多的场景，可以用来生成更多的样例数据，是当前用来解决信息缺失的最好方式。

举一些例子：
Next Video Frame Prediction

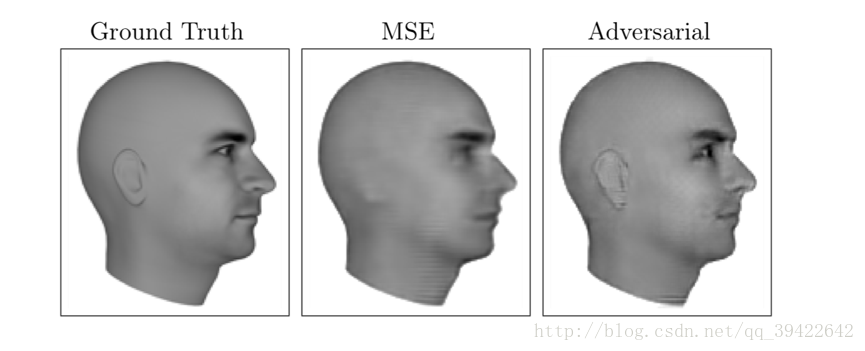
大概意思是预测下一帧会是什么？比如第一个头像是当前帧的状态，然后给出一个MSE（均方差矩阵），预测下一帧会出现什么，如图就是头转了大约15度或者30度左右的样子。

很明显，这个应用是很强大的，比如某些打码的片子，甚者打码的图片，三级片之类的，或者有损失的古物，古画，都有可能通过生成模型，来生成新的。

Single Image Super-Resolution

或者处理比较模糊的图片，因为像素太低，导致人看了不怎么清楚，可以通过GAN来生成更高像素的图片，看的更清晰。上图左为原始图片，第二张为 使用bicubic method的插值法得出的，第三张是使用ResNet,第四张是使用GAN来生成的。

Image to Image Translation

根据你画的样子，给你生成一个你可能想都没想过的样子，或者根据地图，生成场景之类的。

总之，GAN的特点之一，就是生成，生成一些你可能想都没想过的东西。

1-3 生成模型原理—似然原理

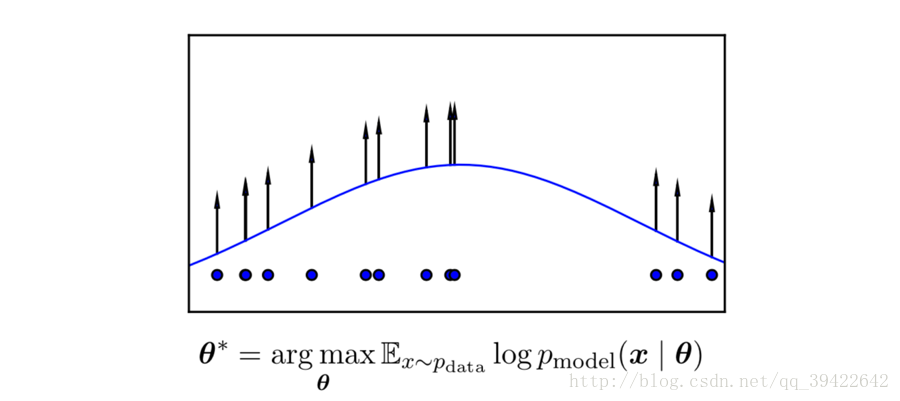
所谓的生成模型，其实就是基于最大似然估计的，而最大似然估计就是用的似然原理。

什么是似然原理呢？我们举个例子，比如你要估计一个学校的数学成绩是多少，肯定不会直接找全校的学生，然后再把他们的数学成绩放在一起计算吧。因为这样做的代价太大了，现实情况根本不允许。

那我们该怎么办呢？
那我们可以随机取样嘛，用样本来估计总体。什么意思呢？我们知道一个群体的某一形状假如服从正态分布，如图所示，那么这个分布的形状由两方面决定，分别是均值$\mu$和方差$\sigma^2$，只要这两个定了，那么图像的概率密度分布也就定了。

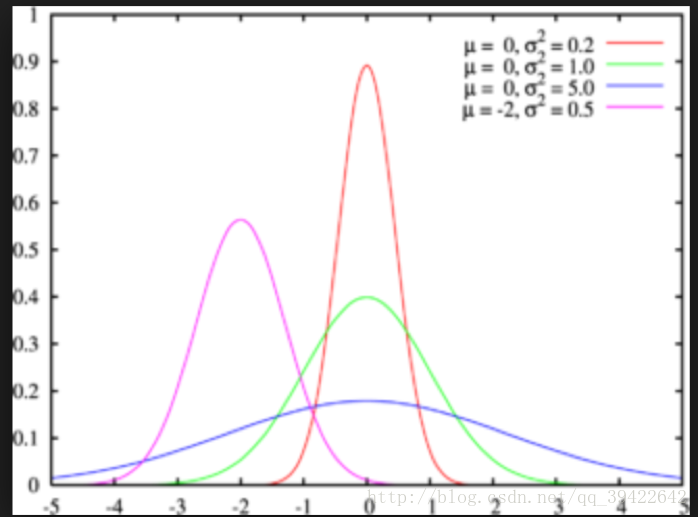
那我们能否用样本（抽到的学生）的均值和方差，估计总体（整个学校的学生）的均值和方差，这样不就得到了总体的概率分布了吗？其实这就是生成模型的原理。
想要详细了解它的公式推导，可以看一下这篇的最后一个部分：概率统计学习基础

2-生成式对抗网络

2-1 生成式对抗网络工作原理

前面我们说的都是前期知识准备，了解生成模型，接下来看一下真正的生成式对抗网络，它的工作流如下：

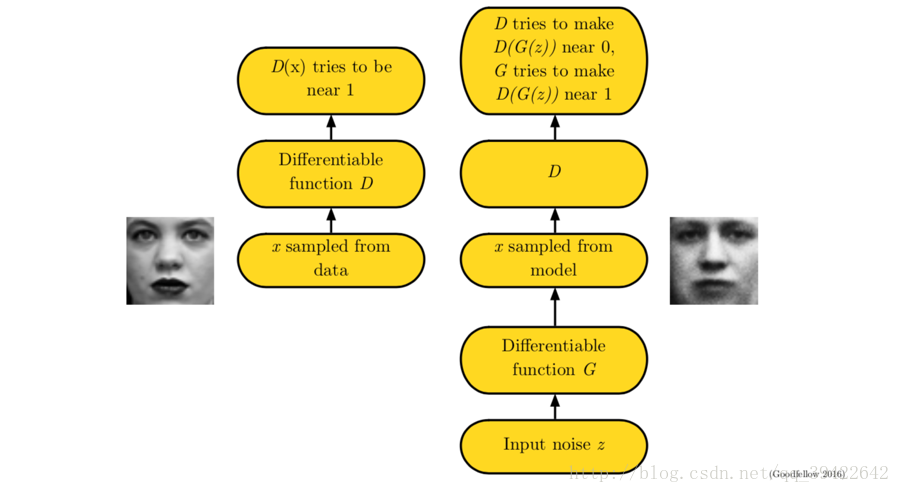
GAN是一种structured probabilistic model，具体介绍在deep learning这本书的第16章有。
顾名思义，生成-对抗，其核心也是两个，一个是生成，用图中的$G(z)$表示，z是隐变量；一个是对抗，用图中的$D(x)$表示，x是观测变量。图结构表示如下：

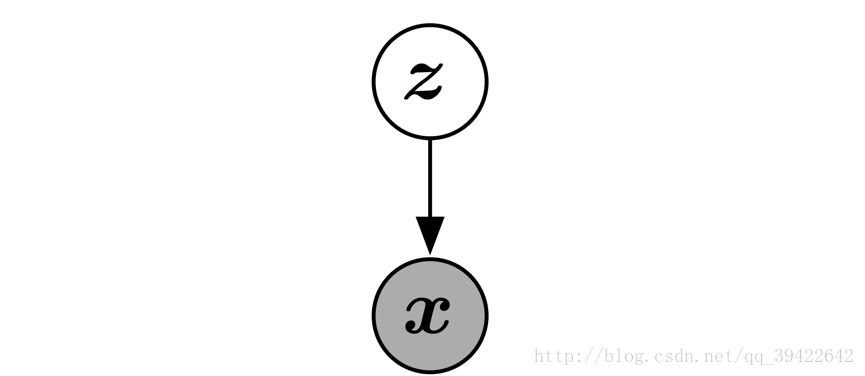
GAN是一个有向图模型，它的每一个隐变量都在影响观测变量。

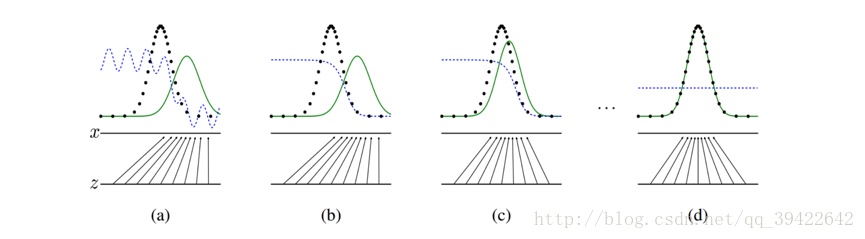
我们希望达到的效果，就如上图所示，生成式对抗网络会训练并更新判别分布（D，图中蓝色虚线部分），希望能将真实的分布（$p_{data}(x),图中黑色虚线$）和生成分布（$p_{model}(G(z)),绿色实线$）区分开来。z表示属于某一分布的噪声数据，经过生成器之后，变成$x = G(z)$,得到一个生成分布$p_{model}(G(z))$。而上方的x水平线则代表真实的分布X中的一部分。

主要目标就两个：

• 判别器$D(x)$独自训练自己，希望能分辨出真实的数据分布和生成器给的数据分布
• 生成器$G(z)$也训练自己，希望以假乱真，让判别器判别不出到底哪个是真，哪个是假

$G(z)$，$D(x)$它们的区别主要在于输入的数据和参数：$\theta^{(G)},\theta^{(D)}$.

我们输入noise样本给