摘要
本文研究以下两个挑战:
1. 如何聚类多视图数据
2. 如何在无参数选择情况下聚类
为此,提出了一种新的目标函数,将原始数据投影到一个空间中,其中投影包含几何一致性(GC)和聚类分配一致性(CAC)。GC的目标是从一个投影空间中学习一个连接图,其中的数据点当且仅当它们属于同一集群时,它们才是连接的。CAC的目的是尽量减少基于视图共识假设的不同视图引起的成对连接图的差异。不同的视图可以产生相同的集群分配结构,因为它们是同一个对象的不同肖像。由于从连接图中获得的视图共识,本文方法可以在学习视图特定表示和消除不同视图之间的异构差异方面取得良好的性能。
1.介绍
聚类分析的目的是根据未标记数据的内在相似性将其分为不同的聚类。几乎所有的多视图聚类方法都必须寻求包括期望簇数在内的最优参数组合,以便获得理想的数据分区。为了寻找最优参数,本文使用了一些评价指标,如标准化互信息NMI(基于标签信息)。在实际中,获取标签信息和预期的聚类数是艰巨的任务,特别在大数据时代。
为了克服上述具有挑战性的问题,本文提出了一种新的多视图聚类方法,称为CrOss-view MatchIng Clustering (COMIC),它可以以数据驱动的方式自动学习几乎所有的参数,包括预期的聚类数。简言之,COMIC将每个数据点投射到一个满足两个属性的空间中(GC和CAC,它们是为不同的目标而设定的)。具体来说,GC的目标是利用局部几何一致性
W
(
v
)
W^{(v)}
W(v)在学习投影空间中对第
v
v
v个视图学习一个标准化的连接图
S
(
v
)
S^{(v)}
S(v)。注意,GC并不像现有的研究那样为每个数据点学习一个紧凑的表示。相比之下,表示
Z
(
v
)
Z^{(v)}
Z(v)是从环境空间中学习出来的,理论上
Z
(
v
)
Z^{(v)}
Z(v)会塌陷成少量的地标,从而得到可解释的结果。简言之,由于学习到的表示法具有相同的输入空间维数,因此本文的方法具有可解释的数据划分和表示法。与GC不同的是,CAC通过最小化连接图
{
S
(
v
)
}
v
=
1
m
\{{S^{(v)}}\}^{m}_{v=1}
{S(v)}v=1m的差异被用来处理多视图数据。换句话说,与大多数传统方法不同,本文的方法采用了一个端到端管道来显式地优化表示及其关系,并将其表示为一个连接图。通过在连接图上强制视图共识而不是学习表示,本文的方法包含以下优点。如图1所示,即使采用了一个成熟的表示学习算法,学习表示法
Z
(
v
)
Z^{(v)}
Z(v)的值在数据视图中可能会有显著的不同。如果尽可能相似地强制视图特定表示,优化可能被扭曲,并可能丢失有用的信息,从而产生较差的聚类性能。相比之下,通过使用
Z
(
v
)
Z^{(v)}
Z(v)之间的连接关系作为不变性,并尽可能地强制接近它们,本文的方法可以在很大程度上避免扭曲表示,从而增强数据聚类。这种想法很容易理解。如果两个对象属于同一个类,它们的连接关系对不同视图和不同投影空间是不变的。
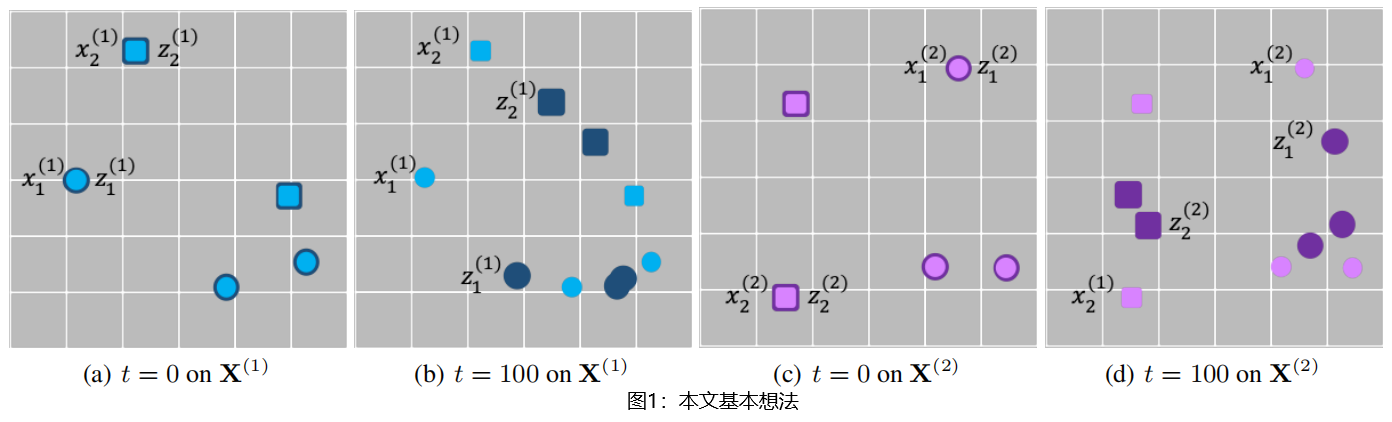
图1:本文基本想法。假设有来自两个视图的5个数据点,每个视图由两个集群(矩形和圆形)组成。浅色点表示原始数据点
{
X
(
v
)
}
v
=
1
2
\{{X^{(v)}}\}^{2}_{v=1}
{X(v)}v=12,深色点表示相应的表示
{
Z
(
v
)
}
v
=
1
2
\{{Z^{(v)}}\}^{2}_{v=1}
{Z(v)}v=12。初始化时
(
t
=
0
)
(t=0)
(t=0),
X
(
v
)
=
Z
(
v
)
X^{(v)}=Z^{(v)}
X(v)=Z(v)。模型收敛后,表示应incorporate the discrimination。本文的想法是双重的。一方面,一个良好的表示可能有助于解决线性不可分割的问题。另一方面,在实现交叉视图共识方面,每一个单个视图的连接图
S
(
v
)
S^{(v)}
S(v)将比视图特定表示
Z
(
v
)
Z^{(v)}
Z(v)更具有鲁棒性且更好。换言之,本文强制连接图
{
S
(
v
)
}
v
=
1
m
\{{S^{(v)}}\}^{m}_{v=1}
{S(v)}v=1m尽可能相似。这种交叉视角的共识学习范式与现有的研究有显著的不同,后者通常要求
{
Z
(
v
)
}
v
=
1
m
\{{Z^{(v)}}\}^{m}_{v=1}
{Z(v)}v=1m尽可能相似。
2.无参数选择的交叉视图匹配聚类
对于一个给定的数据集
X
(
v
)
=
[
x
1
(
v
)
,
x
2
(
v
)
,
.
.
.
,
x
n
(
v
)
]
∈
R
D
(
v
)
×
n
(
v
)
X^{(v)}=[x^{(v)}_1,x^{(v)}_2,...,x^{(v)}_n]\in\mathcal{R^{D^{(v)}×n^{(v)}}}
X(v)=[x1(v),x2(v),...,xn(v)]∈RD(v)×n(v),
X
(
v
)
X^{(v)}
X(v)表示从第
v
v
v个视图采样的数据集,这里有m个不同的视图,提出的目标函数如下:
L
=
∑
v
L
1
(
v
)
+
L
2
(1)
L=\sum_v{L^{(v)}_1}+L_2\tag{1}
L=v∑L1(v)+L2(1)
其中
L
1
(
v
)
L^{(v)}_1
L1(v)和
L
2
L_2
L2分别测量每个单一视图和交叉视图中的损失。确切地说,


其中
z
i
(
v
)
∈
R
D
z^{(v)}_i\in\mathcal{R^D}
zi(v)∈RD是
x
i
(
v
)
x^{(v)}_i
xi(v)的学习表示,目的是保持两个属性,即单个视图中的几何一致性和不同视图中的聚类分配一致性。
W
(
v
)
W^{(v)}
W(v)是一个预先计算好的相似度图来实现几何一致性。本文利用k最近邻的相互连通性(m-kNN)去计算
W
(
v
)
W^{(v)}
W(v),稍后会详细说明。对称矩阵
S
(
v
)
S^{(v)}
S(v)是学习到的连接图,其中被连接的数据点被认为是同一簇的。
λ
(
v
)
\lambda^{(v)}
λ(v)和
μ
(
v
)
\mu^{(v)}
μ(v)是平衡这些项的惩罚参数,这些参数会从下一节提到的数据中学习出来。
L 1 ( v ) L^{(v)}_1 L1(v)和 L 2 L_2 L2是为不同的目的而设计的。直观讲, L 1 ( v ) L^{(v)}_1 L1(v)的目的是学习每个单一视图的 Z ( v ) Z^{(v)} Z(v)和 S ( v ) S^{(v)} S(v),采用流形上的几何一致性。相比之下, L 2 L_2 L2的目的是尽量减少连接图 { S ( v ) } v = 1 m \{{S^{(v)}}\}^{m}_{v=1} {S(v)}v=1m的差异,因为不同的视图应该生成相同的连接构成。更具体地说, L 1 ( v ) L^{(v)}_1 L1(v)包括重建损失和GC约束。重建损失的性能类似于最近的凸聚类(2011、2015、2017),这个方式是在环境空间里为 X ( v ) X^{(v)} X(v)学习 Z ( v ) Z^{(v)} Z(v)。这个想法的动机是,所有集群内的数据点都被高度鼓励去塌陷到少量地标的集合。为了便于聚类,本文提出了GC约束来学习连接图 S ( v ) S^{(v)} S(v),同时强制 Z ( v ) Z^{(v)} Z(v)位于 W ( v ) W^{(v)} W(v)产生的流形上。注意, S i j ( v ) − 1 S^{(v)}_{ij}-1 Sij(v)−1发挥三个作用。首先,它将忽略连接 ( i , j ) (i,j) (i,j),当连接建立 ( S i j ( v ) → 1 ) (S^{(v)}_{ij}→1) (Sij(v)→1)时趋于0,当连接解除 ( S i j ( v ) → 0 ) (S^{(v)}_{ij}→0) (Sij(v)→0)时作为一个惩罚。其次, 连接图的权重被限制在 [ 0 , 1 ] [0,1] [0,1]范围内,以避免由不同的视图引起的尺度差异。第三,它可以避免诸如 S ( v ) = 0 S^{(v)}=0 S(v)=0和 Z ( v ) = X ( v ) Z^{(v)}=X^{(v)} Z(v)=X(v)等无用解
2.1.优化法
为了优化
Z
(
v
)
Z^{(v)}
Z(v)和
S
(
v
)
S^{(v)}
S(v),本文采用了交替最小化策略。具体地说,当
Z
(
v
)
Z^{(v)}
Z(v)固定时,计算等式
1
1
1中
S
i
j
(
v
)
S^{(v)}_{ij}
Sij(v)的导数,如下所述:
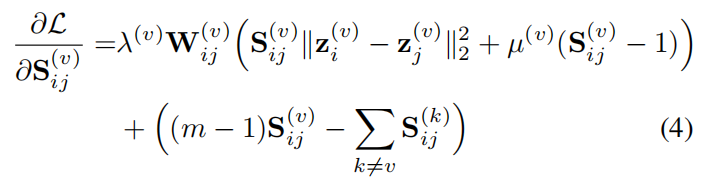
让等式
4
4
4等于0,然后更新
S
(
v
)
S^{(v)}
S(v)通过
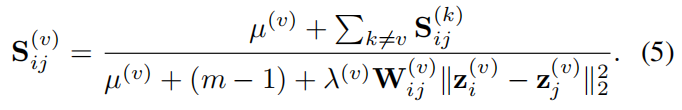
由于
∑
k
≠
v
S
i
j
(
v
)
=
m
−
1
\sum_{k≠v}S^{(v)}_{ij}=m-1
∑k=vSij(v)=m−1,可以看到,如果数据点
x
i
(
v
)
x^{(v)}_i
xi(v)和
x
j
(
v
)
x^{(v)}_j
xj(v)足够接近(即属于同一个簇),那么来自等式
5
5
5的
S
i
j
(
v
)
→
1
S^{(v)}_{ij}→1
Sij(v)→1;否则,
S
i
j
(
v
)
→
0
S^{(v)}_{ij}→0
Sij(v)→0。当
S
(
v
)
S^{(v)}
S(v)固定时,从等式中去掉包括一些项包括等式
3
3
3中的
S
(
v
)
S^{(v)}
S(v),并重写如下:
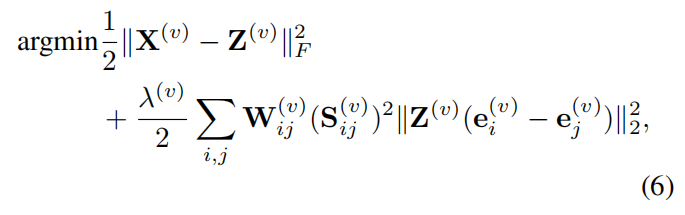
其中
e
i
e_i
ei是一个第
i
i
i项为1的指标向量。这个问题可以有效解决,通过
Z
(
v
)
M
(
v
)
=
X
(
v
)
,
(7)
Z^{(v)}M^{(v)}=X^{(v)},\tag{7}
Z(v)M(v)=X(v),(7)
其中
M
(
v
)
=
I
(
v
)
+
λ
(
v
)
Ω
(
v
)
,
(8)
M^{(v)}=I^{(v)}+\lambda^{(v)}\Omega^{(v)},\tag{8}
M(v)=I(v)+λ(v)Ω(v),(8)
Ω
(
v
)
=
∑
i
,
j
W
i
j
(
v
)
(
S
i
j
(
v
)
)
2
(
e
i
(
v
)
−
e
j
(
v
)
)
(
e
i
(
v
)
−
e
j
(
v
)
)
T
\Omega^{(v)}=\sum_{i,j}{W^{(v)}_{ij}(S^{(v)}_{ij})^2(e^{(v)}_i-e^{(v)}_j)(e^{(v)}_i-e^{(v)}_j)^T}
Ω(v)=∑i,jWij(v)(Sij(v))2(ei(v)−ej(v))(ei(v)−ej(v))T和
I
(
v
)
I^{(v)}
I(v)是一个恒等矩阵。为了有效解决上述问题,需要用到以下定理。
定理 1. 等式
8
8
8中定义的
M
(
v
)
M^{(v)}
M(v)是一个对称的正半定矩阵。(证明暂略)
2.2.初始化和实施的细节
2.3.数据驱动的参数选择
3.相关工作
3.1.凸聚类
3.2.多视图聚类
4.实验
4.1.实验设置
4.2.与最先进的技术比较
4.3.交叉聚类算法的泛化
4.4.可视化分析
4.5.收敛性分析
5.总结
所提出的COMIC算法在实际应用中可以解决两个具有挑战性的问题,即多视图数据的聚类和不考虑聚类大小的聚类。现有的多视图聚类算法与COMIC的一个主要区别是,后者在视图特定的连接图上实现了交叉视图的共识,而不是视图特定的表示。大量实验证明,这种学习范式有效。在未来,为了进一步促进性能,本文作者计划研究COMIC的监督和深度拓展,以利用可用的标签和深度神经网络。





















 5652
5652











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








