离散数学-群和环

半群和独异点

代数系统是由一个非空集合加上一个或几个运算构成的。
从这节起，我们要介绍一些特殊的代数系统。所谓特殊，是指这些代数系统中的运算具有特殊的性质。我们要介绍下列一-些代数系统:
1.半群：
定义:设S是非空集合，★是S上的二元运算，如果★在S上满足封闭性、可结合性，则称<S,*>是半群。
2.独异点：
设<M,★>是个半群，如果★运算有幺元，则称<M,★>是独异点，也称它是含幺半群。





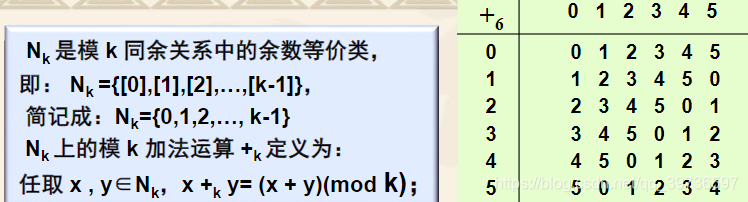
3、可交换半群
设<S,★>是半群，如★是可交换的，则称<S,★>是可交换半群。
4、可交换独异点
<M,★>是独异点，如★是可交换的，则称<M,★>是可交换独异点。
例: <R,+>, <N,X>, <P(E),∩>, <P(E),对称差>都是可交换半群,亦是可交换独异点。
5.子半群
<S,★>是个半群，B⊆S，如果★在B上封闭，则称<B,★>是<S,★>的子半群。
例: <N,+> 是<I,+>的子半群
6.子独异点
<M,★>是个独异点， B⊆M,如果★在B上封闭，且幺元e∈B，则称<B,★>是<M,★>的子独异点。
例: <I,+> 是<R,+>的子独异点。

设<M,★>是可交换独异点，A是M中所有幂等元构成的集合，则<A,★>是<M,★>的子独异点。
显然A⊆M，若要证明<A,+>是<M,★>的子独异点，根据子独异点定义，只需证明么元e∈A以及封闭性即可。

要证明封闭，需要证明集合里面任意两个元素做运算，要证明这个运算仍然在A里面，

群的定义及性质

1.群的定义

群是抽象代数中最重要的代数系统。

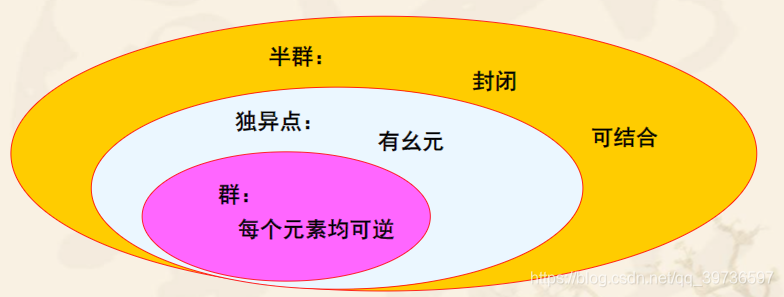
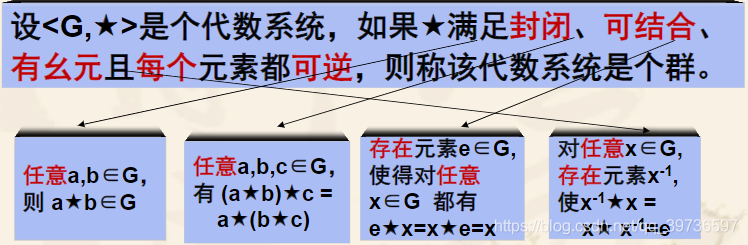
1.群的定义:设<G,★>是代数系统，如果★运算在G上满足封闭性、可结合性、<G,★>中有幺元且G中的每个元素均可逆，则称<G,★>是群。
(1) 设<G,★>是群，若集合G是有限集，则称<G,★>是有限群。反之称为无限群。
(2)只含有幺元的群叫平凡群。
(3)若★运算是可交换的，则称<G,★>是交换群或阿贝尔(Abel)群

<R,+>、<P(E),⊕>是否是群?
<R,+>是独异点，幺元是0，对任意实数r,它的逆元是-r。
<P(E)，⊕>幺元是∅，因对任意集合A∈P(E)，A⊕A=中,
所以A-1=A，所以它们都是群。

<R,X>是独异点，幺元是1，零元是0。因为0没有逆元，所以<R,X>不是群。
<P(E),∩>是独异点，幺元是E。对任意集合A∈P(E)且A不等于全集E，是否有这样的集合使得A∩?=E?
没有这样的集合，即A没有逆元。所以<P(E),∩>不是群。

2.群的性质

群除了具有封闭、可结合、有幺元、每个元素均可逆这四个性质外，还有一-些其它性质。

1.群中无零元

设<G,★>是群，如果|G|>=2， 则G中无零元。
证明: ( 反证法)假设G中有零元θ，则对任何x∈G,有θ★x=x★θ=θ≠e,所以零元θ就不存在逆元,这与<G,★>是群矛盾。所以群<G,★>中无零元。
如果一个代数系统既有零元又有幺元，则幺元和零元一定不能相等。

2.群中每个元素均是可消去元。

设<G,*>是个群，则对任何a,b,c∈G，如果有
(1)a★b= a★c则b=c。
(2)b★a= c★a则b=c。
证明可以用定义证明，也可以用定理去证明。
用定理可以用如下定理
定理:设★是X上可结合的二元运算，如果a∈X,，且a-1∈X，则a是可消去元。

3.群中除幺元外，无其它幂等元。

设<G,★>是群，则G中除幺元外，没有其它幂等元。
证明:(反证法)假设有a∈G是幂等元，即a★a=a于是有a★a=a★e，由可消去性有a=e,所以群中除幺元外，无其它幂等元。

4.群方程有唯一解

设<G,★>是个群，则对任何a,b∈G,
(1)存在唯一元素x∈G，使得a★x=b …（1）
(2)存在唯一元素y∈G，使得y★a=b …（1）
思考：
方程a★x=b的解为a-1★b
方程y★a=b的解是什么?b★a-1

5.有限群运算表的特征

设<G,★>是有限群，则G中每个元素在★运算表中的每一行(列)都必出现且仅出现一次。

<G,★>是个群，对任何a,b∈G,有
(1) (a-1)-1=a
(2) (a★b)-1= b-1★a-1

群的阶与群中元素的阶

1.群的阶:
定义:设<G,★>是群，如果|G|=n，则称<G,★>是n阶群。
当G所包含的元素个数为有限时，群<G,★>的阶为G所包含的元素个数。
当G所包含的元素个数为无限时，群<G,★>为无限群。

从运算表可以看出:所有的一阶群都同构;所有的二阶群都同构;
所有的三阶群都同构。

2.群中元素的阶
定义:设<G,★>是群，a∈G，使得ak=e成立的最小正整数k称为a的阶，记作|a|=k,称a为k阶元。
若不存在这样的正整数k，则称a的阶是无限的。
如整数上的加法是无限的。
例如:群<I,+>是一个无限群，只有幺元0的阶是1，其余元素的阶都是无限的。
例: <X, o>的运算表如下图所示: <X, o>是否是群?若是群求各元素的阶。

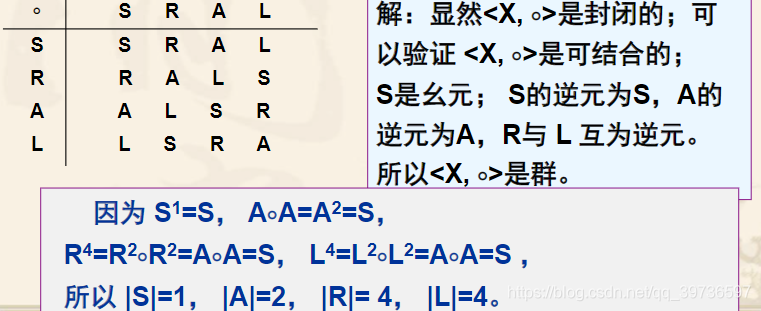
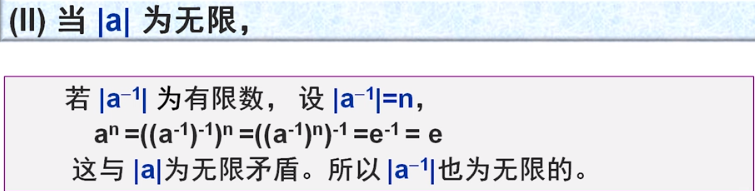
设<G,★>是群，a∈G且|a|=k。设n是整数，则
(1)an=e当且仅当k/n
(2)|a-1|= |a|

子群及其证明

群的定义

子群的定义

设<G,★>是群，S是G的非空子集，如果<S,★>满足:
(1)对任何a,b∈S,均有a★b∈S; (封闭)
(2)幺元e∈S;(有幺元)
(3)对任何a∈S,有a1∈S(可逆)
则称<S,★>是<G,★>的子群。
子群：应该是原群的非空子集，本身也应该是一个群

任何群<G,★>都存在子群，<{e},★>及<G,★>都是<G,★>的子群，称为<G,★>的平凡子群。
平凡群是指<{e},★>，只有幺元e的集合。
例:代数系统<R,+>是群，代数系统<I,+>是<R,+>的子群。
因为I⊆R，任意两个整数做加法运算仍然是整数;幺元0∈l;对每个x∈l,其逆元-x∈I

子群的证明

用子群的定义证明:
即证明运算在非空子集上满足封闭性、有幺元、子集中每个元素均可逆。

子群判定定理1:（有限封闭）

设<G,★>是群，B是G的有限子集，如果★在B上满足封闭性，则<B,★>是<G,★>的子群。

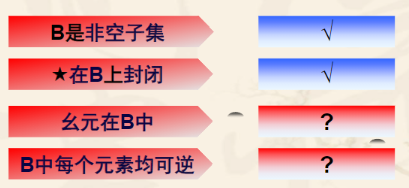
(1)先证明幺元e∈B

(2)再证B中每个元素均可逆,任意b∈B,都有b-1∈B。

综上，<B,★>是<G,★>的子群。

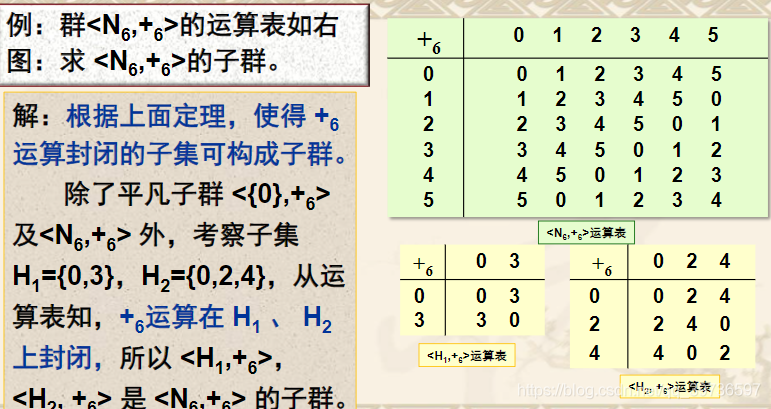
子群判定定理2:

设<G,★>是群，S是G的非空子集，如果对任意a,b∈S，均有a★b-1∈S,则<S,★>是<G,★>的子群。

(1)先证幺元e∈S

(2)再证S中任意元素均可逆

(3)最后证明<S,★>的封闭性,任意a,b∈S,都有a★b∈S

综上，<S,★>是<G,★>的子群。
练习:已知<H1,★>和<H2,★>是群<G,★>的子群，求证<H,∩H2,★>是<H1,★>、<H2,★>和<G,★>的子群。

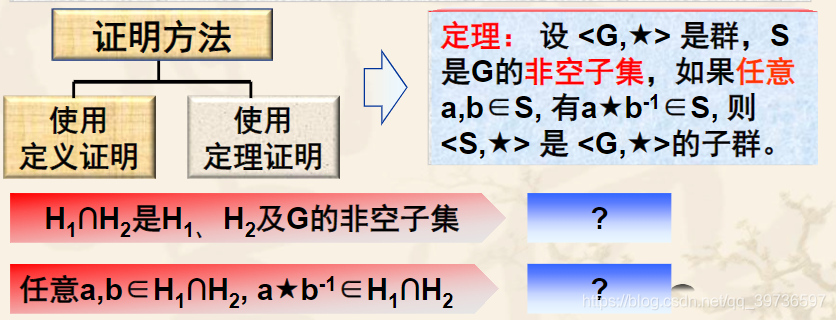
(1)先证明H1∩H2是H1，H2及G的非空子集
显然H1∩H2⊆H1, H1∩H2⊆H2,
H1∩H2⊆G;
因为<H1，★>和<H2,★>是群<G,★>的子群，所以幺元e∈H1并且e∈H2,
于是e∈H1∩H2,即H1∩H2≠∅
所以H∩H2是H1、H2及G的非空子集。
(2)再证明对任意a,b∈H1∩H2，a★b-1∈H1∩H2

子群的陪集及拉格朗日定理

子群的陪集

1.定义:设<H,★>是群<G,★>的子群，a∈G，定义集合:
aH={a★h|h∈H}
Ha={h★a|h∈H}
称aH(Ha)为a确定的H在G中的左(右)陪集。
我们只讨论左陪集，对于右陪集有相似的结论

定理1:两个陪集要么相等，要么不相交

<H,★>是群<G,★>的子群，任何a,b∈G,有
(1)aH=bH当且仅当a∈bH
(2)aH∩bH=中当且仅当a∉bH
a)必要性，已知aH=bH，因e∈H,于是a=a★e∈aH，所以a∈bH。



从上面定理可以看出:一个子群的任意两个左陪集，要么相等，要么不相交。
当a∈bH,aH=bH ;
当a∉bH,aH∩bH=∅。

定理2：a仅属于一个陪集

设<H,★>是群<G,★>的子群，对任何a∈G,a必属于且仅属于一个陪集。

定理3：陪集任何两个元素都不相同

设<G,★>是有限群，<H,★> 是群<G,★>的子群，b∈G,bH为<H,★>的左陪集，则bH中的任何两个元素都不相同。

(反证法，假设bH中有两个元素相同)
假设有b★h1∈bH，b★h2∈bH，(其中h1,h2∈H,h1≠h2)使得b★h1=b★h2，由可消去性有h1=h2,矛盾。所以bH中任何两个元素都不相同。

拉格朗日定理：群的阶是子群的阶的整数倍

设<G,★>是有限群，|G|=n, <H,★>是<G,★>的任意子群，|H|=m,则n=km (k∈l)。
拉格朗日定理描述的内容是群的阶是子群的阶的整数倍
群的阶数指的是群中元素的个数。

拉格朗日定理说明:n阶群的子群阶数是群阶数的因子。

下面的推论1说明:
群中元素的阶数必是群阶数的因子。

循环群

1.定义:

设<G,★>是群，如果存在一一个元素g∈G，对任意x∈G，都存在整数i,使得x=gi，则称<G,★>是循环群。并称g是G的生成元。
所有的元素都可以通过其中一个元素幂指形式生成。


思考：-1是否是生成元?

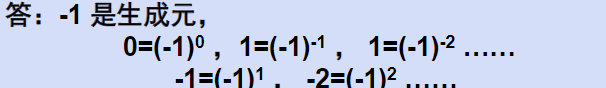
2.循环群的类别:

根据生成元g的阶，循环群<G,★>可以分成两类:

定理

设<G,★>是以g为生成元的有限循环群。则|G|=n
当且仅当|g|=n

循环群中生成元的个数

设<G,★>是由g生成的循环群。
(1)若G为无限循环群，则G只有两个生成元g和g-1。
(2)若G是n阶循环群，则G含有φ(n)个生成元。
对于任何正整数r,若r≤n且与n互素,
则gr是G的生成元。
φ(n)为欧拉函数，即小于或等于n且与n互素的正整数的个数。
证明：(1)若G为无限循环群，则G只有两个生成元g和g-1。

证明：(2)若G是n阶循环群，则G含有φ(n)个生成元


一般来说，求一个群的子群并不容易，但对于循环群，可以直接求出他的所有子群
<G,★>是由g生成的循环群，|G|=12,
小于或等于12且与12互素的正整数有4个:
1,5,7,11，即φ(12)=4。于是<G,★>有4个生成元，分别是:g,g5,g7, g11

设<G,+>， G={3a| a∈I}，+是普通加法运算，则<G,+>为无限循环群,只有两个生成元: 3和-3。

循环群的子群

(1)若<G,★>循环群，则<G,*>的子群仍是循环群。.
(2)若<G,★>是无限循环群，则<G, ★>的子群除<{e},★>以外都是无限循环群。
(3)若<G,★>是n阶循环群，则对n的每个正因子d,<G,★>恰好含有一个d阶子群。

证明：(1)若<G,★>循环群，则<G,*>的子群仍是循环群
主要是找到生成元



设<G,★>是素数阶群，则它无非平凡子群，并且它必是循环群。