定义10.1
(1) 设V=<S, ∘ >是代数系统,∘为二元运算,如果∘运算是可结合的,则称V为半群.
(2) 设V=<S,∘>是半群,若e∈S是关于∘运算的单位元,则称V是含幺半群,也叫做独异点. 有时也将独异点V 记作 V=<S,∘,e>.
(3) 设V=<S,∘>是独异点,eS关于∘运算的单位元,若 aS,a1S,则称V是群. 通常将群记作G.
定义10.2 (1) 若群G是有穷集,则称G是有限群,否则称为无限群. 群G 的基数称为群 G 的阶,有限群G的阶记作|G|.
(2) 只含单位元的群称为平凡群.
(3) 若群G中的二元运算是可交换的,则称G为交换群或阿贝尔 (Abel) 群.
定义10.3 设G是群,a∈G,n∈Z,则a 的 n次幂.
定义10.4 设G是群,a∈G,使得等式 ak=e 成立的最小正整数k 称为a 的阶,记作|a|=k,称 a 为 k 阶元. 若不存在这样的正整数 k,则称 a 为无限阶元.
定理10.1设G 为群,则G中的幂运算满足:
(1) a∈G,(a1)1=a
(2) a,b∈G,(ab)1=b1a1
(3) a∈G,anam = an+m,n, m∈Z
(4) a∈G,








 本文介绍了群和环的数学概念,包括半群、独异点、群的性质,如结合律、幂运算、消去律,以及子群的定义和判定定理。此外,还探讨了环的概念,包括加法和乘法的性质,以及交换环、含幺环和无零因子环的特性。
本文介绍了群和环的数学概念,包括半群、独异点、群的性质,如结合律、幂运算、消去律,以及子群的定义和判定定理。此外,还探讨了环的概念,包括加法和乘法的性质,以及交换环、含幺环和无零因子环的特性。
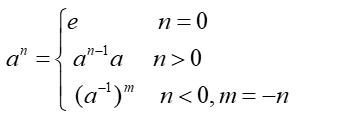
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 6902
6902

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








